|
DOI: 10.7256/2453-8809.2017.3.24563
Received:
28-10-2017
Published:
28-03-2018
Abstract:
The object of the research is the process of a work tool of a tillage machine with a flexible element getting into contact with the soil. The subject of the research is a physical model that allows to analyze the process of a work tool with a flexible element getting into contact with the soil and mechanical and technological methods of improving the process of soil cultivation. The cable with a cross section area in a form of a circle is viewed as a wedge with a dull edge. The authors of the article pay special attention to the theory of granular medium statics. The extreme limit state at which even the slightest change in the volume and surface forces distorts the balance of the granular medium is especially interesting and useful for composing mathematical models of a work tool getting into contact with theh soil because pressure forces reach the highest point at such moments. The authors carried out their theoretical research using the method of the mathematical mechanical modelling of work tools getting into contact with the soil. The authors discover the dependence of the wedge cutting pressure on the cutting angle and depth. They prove that when the cutting angle is reduced, the cutting pressure of the soil goes down to the minimum at first but grows endlessly afterwards. The soil cutting effort is composed of two elements, the soil destruction effort and the effort to overcome the frictional force of the soil against the wedge. When the cutting angle is reduced, the soil destruction effort decreases while the effort to overcome the frictional force of the soil against the wedge increases. The sum of these two elements is equal to the minimal effort of the wedge cutting the soil.
Keywords:
internal friction angle, elementary area length, extreme limit state, dependence of cutting pressure, normal stress, process, wedge, draft resistance, work tool, weed control
Введение. Поверхностная обработка почвы проводится с целью крошения пласта ее верхнего слоя, измельчения пожнивных остатков, уничтожения сорных растений и выравнивания поверхности поля.
В 20-е годы прошлого столетия в условиях засухи проявлялся особый интерес к вопросам так называемого сухого земледелия, обеспечивающего накопление и сбережение почвенной влаги. Для этого успешно применялись чистые пары, которые даже в условиях засухи позволяли получать неплохие результаты при возделывании озимых зерновых, за что в то время их называли "водозапасными магазинами". Однако многократные обработки чистых паров традиционными культиваторными лапами, вызванные необходимостью уничтожения сорных растений, в результате чрезмерного перемешивания поверхностных слоев способствовали увеличению потерь влаги. При наблюдении за работой различных орудий на пару было замечено, что при своевременной обработке почвы даже рабочие органы с тупым лезвием хорошо уничтожали нежные всходы сорных растений. В связи с этим в то время и появилась идея замены рабочих органов с тупым лезвием проволокой, имеющей минимальную поверхность трения [1]. Орудия, в которых использовалась проволока, называли в то время пароочистителями. Для этого на раме конного культиватора или плуга устанавливались три ножевидные стойки — одна впереди и две сзади. Между ними под углом 60° натягивалась металлическая проволока диаметром 3 мм. Глубина обработки почвы проволокой равнялась примерно 10 см.
Проходил испытание пароочиститель на Полтавской опытной станции на протяжении всего сезона в засушливых 1924 и 1925 годах. К положительным сторонам орудия были отнесены низкая металлоемкость, простота конструкции, доступность для всех даже мелких крестьянских хозяйств, хорошая работа по срезанию сорных растений с глубоко сидящей корневой системой (березка, осот, лебеда и др.) и низкая энергоемкость в работе. К недостаткам орудия были отнесены сложность регулировки глубины хода проволоки, оставление несрезанными мелко растущих сорных растений, забивание стоек растительными остатками и возможность обрыва проволоки.
Однако, несмотря на положительные результаты двухлетних испытаний проволочного рабочего органа на Полтавской опытной станции, широкого применения в условиях производства он не получил. На наш взгляд, это связано с тем, что в те годы не были проведены исследования по изучению возможности повышения его надежности в работе, использования для разноглубинной обработки почвы и в сочетании с другими типами рабочих органов почвообрабатывающих орудий.
Постановка проблемы. Качество обработки почвы может быть улучшено за счет оборудования известных рабочих органов [2] устройством для дополнительного крошения пласта и усиления процесса сепарации ее структурных частиц и корневищ растений. Последнее необходимо для извлечения из почвы корневищ корнеотпрысковых сорняков, что является одним из наиболее эффективных приемов борьбы с ними. Попытка создания орудия для вычесывания и выталкивания на поверхность почвы корневищ сорняков была сделана в 1937 году в Сибирском научно–исследовательском институте зернового хозяйства [3].
Для регулирования агрофизических свойств поверхностного слоя почвы (до 4 см) нами были проведены поисковые исследования по изучению возможности и целесообразности использования проволоки или троса диаметром 2...4 мм, который в дальнейшем будем называть гибким элементом. Схема предполагаемого воздействия гибкого элемента на почву показана на рис. 1.
Визуальные наблюдения за процессом работы гибкого элемента показали, что под его воздействием в почве образуется валок, при движении которого на поверхности поля обеспечивается засыпка микронеровностей почвы. Причем высота валка существенно превышает размеры поперечного сечения гибкого элемента. Исследования показали, что наилучшее качество выравнивания поверхности поля было получено при движении гибкого элемента вдоль гребней. При этом разница в качестве выравнивания поверхности поля при движении гибкого элемента вдоль и под различными углами к гребням настолько велика, что легко определяется даже визуальным способом. Это, по-видимому, объясняется более устойчивым движением гибкого элемента вдоль гребней в связи с большей стабильностью по величине силы сопротивления движению его в почве. Последнее создает хорошие предпосылки для использования его в одном агрегате с другими типами почвообрабатывающих рабочих органов.
Рис. 1. Схема предполагаемого воздействия гибкого элемента на почву
Кроме того, из анализа схемы воздействия на почву гибкого элемента с круглой формой поперечного сечения видно, что он с одновременным рыхлением поверхностного слоя почвы обеспечивает уплотнение ее нижних слоев.
В связи с вышеизложенным, с учетом результатов известных и поисковых исследований, возникла необходимость в разработке предлагаемых рабочих органов почвообрабатывающей машины.
Анализ исследований и публикаций.Прежде, чем приступать к построению математической модели взаимодействия с почвой гибкого элемента почвообрабатывающего рабочего органа, необходимо вскрыть физическую сущность его процесса. Для этого воспользуемся имеющимися гипотезами и результатами исследований Т.М. Гологурского, М.Х. Пигулевского, В.П. Горячкина, Г.Н. Синеокова, А.Н. Зеленина, А. Кулена, А.Н. Панченка и других.
Проволоку с поперечным сечением в виде круга можно рассматривать как одну из равновидностей клина с тупым лезвием. Причем угол крошения почвы в таком клине в каждой его точке не является постоянным и определяется углом наклона касательной к окружности. Известно, что с увеличением угла крошения до величины, когда
 , (1) , (1)
( – угол крошения; – угол крошения;  – угол внешнего трения), почва перестает двигаться по клину и сгруживается впереди него [4]. В этом случае напряжения сдвига на поверхности раздела почва–материал превышают внутреннюю прочность почвы и сдвиг пласта происходит не по поверхности рабочего органа, а в почвенном теле [5].Это является нормальным явлением и не препятствует процессу обработки почвы [6]. Ту часть уплотненной почвы, которая перемещается вместе с рабочим органом, принято называть почвенным ядром. – угол внешнего трения), почва перестает двигаться по клину и сгруживается впереди него [4]. В этом случае напряжения сдвига на поверхности раздела почва–материал превышают внутреннюю прочность почвы и сдвиг пласта происходит не по поверхности рабочего органа, а в почвенном теле [5].Это является нормальным явлением и не препятствует процессу обработки почвы [6]. Ту часть уплотненной почвы, которая перемещается вместе с рабочим органом, принято называть почвенным ядром.
Процесс образования перед штампом почвенного ядра из парафина в песке изучался М.Х. Пигулевским [4]. Было установлено, что при движении штампа перед ним в песке образуется фигура в виде конуса с основанием, равным площади штампа. В связи с этим деформирующим элементом в грунте является не штамп, а конусное почвенное ядро.
На основании проведенных опытов с песком Ратье установил, что почвенное ядро образуется перед режущим профилем с углом заточки большего угла, значение которого составляет около 30°. Последнее было подтверждено в опытах А.Н. Зеленина [6] при изучении процесса образования почвенного ядра в глинистой и суглинистой почвах под воздействием вертикального ножа. Почвенное ядро образовывалось перед ножом с профилем круглого сечения и с углом заточки более 25...30°. В таких случаях Ратье рекомендовал при изучении взаимодействия ножа с грунтом использовать значение коэффициента внутреннего трения. В опытах Ратье с песком наблюдался процесс непрерывной смены частиц почвенного ядра, а А.Н. Зеленин при работе со связными грунтами такого явления не наблюдал. Поэтому можно сделать вывод о том, что быстрота смены частиц почвенного ядра зависит от связных свойств почвы.
Процесс скалывания пласта почвы, то есть отделение его от монолита, под действием клина может происходить путем его сдвига или отрыва. На основании проведенных экспериментальных исследований Т.М. Гологурский, В.П.Горячкин и др. утверждали, что основным видом деформации почвы является сдвиг. Однако позднее в работах В.В. Бородкина и В.Г. Кирюхи-на отмечалось, что суглинистые и глинистые почвы под воздействием клина разрушаются путем отрыва[8]. Г.Н. Синеоков утверждает, что отделение пласта почвы от монолита на песчаных и супесчаных почвах происходит путем сдвига [8]. При воздействии клина на малосвязные почвы сначала она сжимается, а затем вдавливается в недеформируемую массу до тех пор, пока она не достигнет предельного состояния и не произойдет сдвиг пласта. Следовательно, отделение пласта почвы от монолита путем сдвига или отрыва происходит в зависимости от вида почвы и ее состояния. При обработке почвы, находящейся в связном состоянии, отделение пласта почвы от монолита происходит путем отрыва, а для сыпучей среды — путем сдвига.
В экспериментальных исследованиях А.Г. Цымбала [9] было доказано, что черноземная почва с плотностью ниже 0,9 г/см3 при обработке не образовывает комков. Такую плотность почва имеет на прокультивированном поле. А так как рабочий орган с гибким элементом рекомендуется использовать для рыхления и выравнивания поверхностного слоя почвы после или одновременно с культивацией, то для описания процесса взаимодействия его с почвой можно воспользоваться теорией состояния сыпучей среды.
В теории статики сыпучей среды напряжение, при котором небольшое изменение объемных или поверхностных сил вызывает нарушение равновесия сыпучей среды, называется предельным. Последнее представляет наибольший интерес для составления математических моделей взаимодействия рабочего органа с почвой, так как в такие моменты силы давления между ними достигают максимальных величин. История развития теории предельного состояния сыпучей среды описана в работах В.В. Соколовского [6].
Основоположником теории является Ш. Кулон (1773), который впервые сформулировал основные ее положения и применил к определению давлений засыпки на вертикальную стенку с гладкой задней гранью. В. Ренкин в 1857 году ввел понятие о поверхностях скольжения. В дальнейшем С.И. Бельзецкий (1914), Г. Креем (1918), Н.М. Герсеванов (1923), Н.П. Пузыревский (1923) и Флениус (1926) разработали теорию предельного равновесия при допущении существования поверхности сползания простейших форм — плоских, призматических или круглоцилиндрических. В 1934 г. И.П. Прокофьев и Н.И. Безухов развили эту теорию по нахождению положения выбранного тела в состоянии предельного равновесия. Впоследствии они составили графики и таблицы, которые позволяли получить приемлемые результаты для решения некоторых простейших задач.
В 1905 г. Ф. Кеттер и его последователь В. Ренкин, использовав дифференциальные уравнения предельного равновесия в точке, составили систему дифференциальных уравнений сыпучей среды. Приближенные методы решения этой системы уравнений были предложены Т. Капманом и А. Како.
Цель статьи. Определить зависимости усилия резания ножом почвы от угла резания и глубины его хода.
Основной материал. А.Н. Зеленин при рассмотрении теории резания грунтов с применением теории давления сыпучих тел рассматривал сдвигаемое сыпучее тело как твердую среду в состоянии предельного равновесия [10]. Им была получена формула для определения усилий резания ножом сыпучего тела
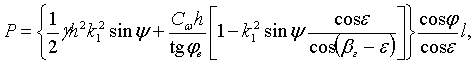 (2) (2)
где 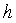 – толщина срезаемой стружки; – толщина срезаемой стружки;
g – плотность почвы;
jв – угол внутреннего трения сыпучей среды;
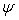 – угол сдвига тела скольжения сыпучей среды, причем – угол сдвига тела скольжения сыпучей среды, причем 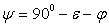 , где , где 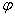 – угол трения между грунтом и клином; – угол трения между грунтом и клином;
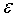 – угол между гранью клина и вертикалью; – угол между гранью клина и вертикалью;
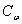 – коэффициент сцепления почвы; – коэффициент сцепления почвы;
bг – угол между плоскостью поверхности засыпки и горизонтом.
Коэффициенты 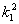 и и 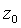 находятся по формулам [10]: находятся по формулам [10]:
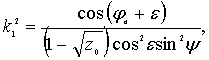
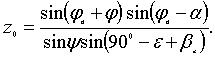
После проведения вычислений А.Н. Зеленин получил график зависимости усилия резания от угла 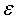 (рис. 2). (рис. 2).
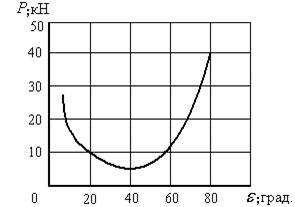
Рис. 2. Зависимость усилия резания почвы
от переднего угла резания ножа 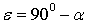
Проанализировав полученную зависимость и сравнив ее значения с результатами экспериментальных данных, А.Н. Зеленин не нашел объяснения увеличению усилий резания до бесконечности при стремлении угла резания почвы ножом к нулю и расхождению в значениях усилия резания. Ссылаясь на полученные результаты и исследования Терцаги, который отмечал несогласованность опытных данных изучения давления грунта на наклонные подпорные стенки с теорией Кулона, А.Н. Зеленин сделал вывод о неприемлемости теории давления сыпучих тел для определения усилия резания грунта клином.
Теория предельного состояния сыпучей среды была использована В.И. Баловневым при моделировании процессов взаимодействия со средой рабочих органов дорожно-строительных машин [13].
Предельное состояние среды с малой прочностью описывается уравнением Кулона
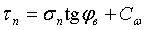 , ,
где 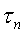 – касательное напряжение в рассматриваемой точке сыпучей среды; – касательное напряжение в рассматриваемой точке сыпучей среды;
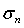 – нормальное напряжение. – нормальное напряжение.
При этом предельное напряжение состояния среды зависит от пределов изменения угла наклона стенки к горизонту [6].
Для пологих стенок с углом наклона ее к горизонту
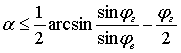 , ,
где 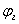 – угол внутреннего трения по горизонтальным плоскостям. – угол внутреннего трения по горизонтальным плоскостям.
Нормальные и касательные напряжения в почве на поверхности стенки вычисляются по формулам
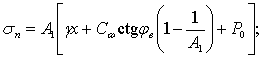
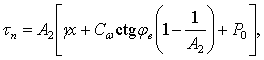
где 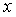 – текущая координата по вертикали; – текущая координата по вертикали;
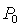 – внешнее давление на поверхность почвы; – внешнее давление на поверхность почвы;
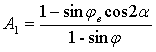 ; ; 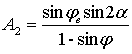 . .
Нормальная составляющая и результирующая элементарной силы определяются по формулам (рис. 3):
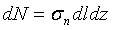 ; ; 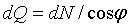 , ,
где 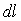 – длина элементарной площадки. – длина элементарной площадки.
Из-за наклона ножа к горизонту длина элементарной площадки определяется по уравнению 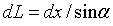 . .
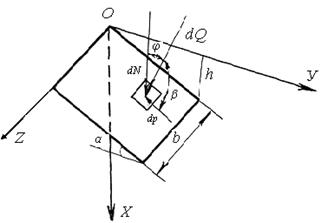
Рис 3. Схема к определению сил, действующих на нож
Элементарная горизонтальная составляющая силы сопротивления движению ножа в почве вычисляется по формуле 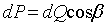 , где , где 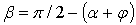 . .
С учетом того, 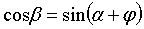 , элементарная горизонтальная сила сопротивления равна , элементарная горизонтальная сила сопротивления равна
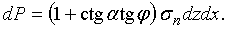 . .
Тогда для ножа с пологим углом наклона к горизонту с учетом выражения для 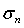 при при 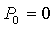 элементарная сила элементарная сила 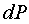 определяется по уравнению определяется по уравнению
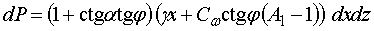 . (3) . (3)
Полученные соотношения описывают закономерности распределения удельных давлений почвы на рабочей поверхности ножа. Однако для определения степени их обоснованности возникла необходимость в сопоставлении этих данных с результатами других исследований по определению усилия резания почвы клином.
Общее тяговое сопротивление клина лобового резания с учетом краевого эффекта, при котором его ширина увеличивается на двойную величину глубины хода (при условии 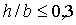 ), определяется путем интегрирования уравнения (3) ), определяется путем интегрирования уравнения (3)
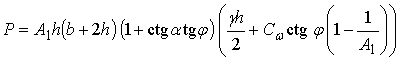 . .
На рис. 4 показана зависимость усилия резания почвы клином от угла резания. Зависимость построена при 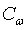 = 0,3 кг/см2; = 0,3 кг/см2; 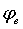 = 39°; g =1,8 г/см3; h= 10 см; b=150 см. = 39°; g =1,8 г/см3; h= 10 см; b=150 см.
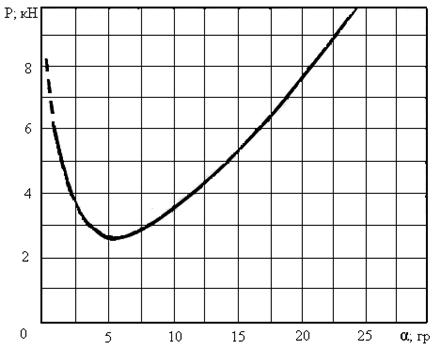
Рис. 4. Зависимость усилия резания лезвием ножа от угла резания
Из рисунка 4 видно, что с уменьшением угла резания усилие резания почвы сначала уменьшается до минимума, а затем резко возрастает до бесконечности. Полученная зависимость имеет хорошее качественное совпадение с результатами исследований А.Н. Зеленина (см. рис. 2). При этом стремление усилия резания при малых углах к бесконечности А.Н.Зеленин считал противоречащим экспериментальным данным. Анализ уравнения показывает, что усилие резания почвы состоит из двух слагаемых: усилия разрушения почвы (слагаемое при коэффициенте 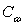 ) и усилия преодоления сил трения почвы о нож (слагаемое при gh/2). С уменьшением угла резания при a=0 слагаемое при ) и усилия преодоления сил трения почвы о нож (слагаемое при gh/2). С уменьшением угла резания при a=0 слагаемое при 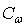 стремится к нулю, а слагаемое при gh/2 — до бесконечно большой величины. Последнее происходит из-за увеличения до бесконечности длины ножа, что и объясняет противоречия, обнаруженные А.Н. Зелениным. Если же рассматривать нож фиксированного размера, то после интегрирования уравнения получим стремится к нулю, а слагаемое при gh/2 — до бесконечно большой величины. Последнее происходит из-за увеличения до бесконечности длины ножа, что и объясняет противоречия, обнаруженные А.Н. Зелениным. Если же рассматривать нож фиксированного размера, то после интегрирования уравнения получим
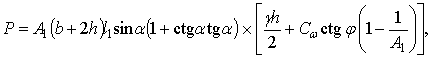
где 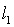 – длина ножа. – длина ножа.
Анализ уравнения показывает, что при 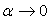 усилие резания не будет стремиться к бесконечности, так как площадь трения почвы о нож не зависит от угла резания. усилие резания не будет стремиться к бесконечности, так как площадь трения почвы о нож не зависит от угла резания.
На рис. 5 показана зависимость усилия резания почвы ножа от угла резания для различной глубины хода. Зависимость, построенная при g = 1,8 г/см3; b= 150 см; 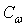 = 0,3 кг/см2; = 0,3 кг/см2; 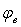 = 39°, качественно хорошо совпадает с результатами эксперимента А.Н. Зеленина [7]. При анализе полученных результатов А.Н. Зеленин только отмечает наличие минимального усилия резания и смещения его в сторону больших значений углов с увеличением глубины хода ножа. Анализ полученного уравнения позволяет объяснить оба эти факта. При уменьшении угла резания усилие (слагаемое при = 39°, качественно хорошо совпадает с результатами эксперимента А.Н. Зеленина [7]. При анализе полученных результатов А.Н. Зеленин только отмечает наличие минимального усилия резания и смещения его в сторону больших значений углов с увеличением глубины хода ножа. Анализ полученного уравнения позволяет объяснить оба эти факта. При уменьшении угла резания усилие (слагаемое при 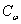 ) на разрушение почвы снижается, а на преодоление сил трения ее о нож (слагаемое при ) на разрушение почвы снижается, а на преодоление сил трения ее о нож (слагаемое при 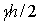 ) — повышается. Равенство этих двух слагаемых соответствует минимальному значению усилия резания почвы ножом. ) — повышается. Равенство этих двух слагаемых соответствует минимальному значению усилия резания почвы ножом.
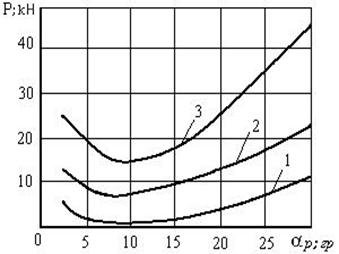
Рис. 5. Зависимость усилия резания лезвием ножа от угла резания
для различной глубины обработки: 1 - h = 0,1 м; 2 – h = 0,2 м; 3 – h= 0,3 м
С увеличением глубины резания почвы величина 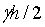 возрастает и равенство двух слагаемых усилия резания достигается при больших значениях угла резания a. На рис. 6 показана зависимость усилия резания от глубины хода ножа при ширине его захвата 50; 80 и 110 см и a = 40°; g = 1,3 г/см3; возрастает и равенство двух слагаемых усилия резания достигается при больших значениях угла резания a. На рис. 6 показана зависимость усилия резания от глубины хода ножа при ширине его захвата 50; 80 и 110 см и a = 40°; g = 1,3 г/см3; 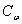 = 0,3 кг/см2; = 0,3 кг/см2; 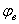 = 29° и j = 21°. Полученные кривые хорошо совпадают с известными эмпирическими зависимостями [10, 11, 12]. = 29° и j = 21°. Полученные кривые хорошо совпадают с известными эмпирическими зависимостями [10, 11, 12].
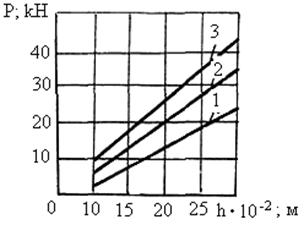
Рис. 6. Зависимость усилия резания лезвием ножа от глубины для
различной ширины захвата ножа: 1 – b= 50 см; 2 – b= 80 см; 3 – b= 50 см
Выводы. Зависимости усилия резания ножом почвы от угла резания и глубины его хода, полученные с помощью уравнений теории сыпучих сред, имеют качественные совпадения с результатами других исследователей.
References
1. Soshal'skii P.N. Provolochnyi paroochistitel'. – Poltava, 1926. – S.15.
2. Syromyatnikov Yu.N. Povyshenie effektivnosti tekhnologicheskogo protsessa dvizheniya pochvy po lemekhu pochvoobrabatyvayushchei rykhlitel'no-separiruyushchei mashiny. // Sel'skoe khozyaistvo. — 2017.-№ 1.-S.48-55. DOI: 10.7256/2453-8809.2017.1.22037. URL: http://e-notabene.ru/sh/article_22037.html
3. Tarchevskii A.V. Pal'tsevyi rotatsionnyi kul'tivator // Mekhanizatsiya sotsialisticheskogo sel'skogo khozyaistva. – 1937. – № 6. – S. 45.
4. Zaitseva A.A. Bor'ba s vetrovoi eroziei pochv. – M.: Kolos, 1970. 152 s.
5. Smirnov V.I., Krylov V.I., Kantorovich L.V. Variatsionnoe ischislenie. – L., 1933. – 204 s.
6. Sokolovskii V.V. Statika sypuchei sredy. 3-e izd. – M.: Fiz-matizdat, 1960. – 244 s.
7. Goryachkin V.P. Sobranie sochinenii. T. 1. 2–e izd. – M.: Kolos, 1968. – 719 s.
8. Sineokov G.N., Panov I.M. Teoriya i raschet pochvoobrabatyvayushchikh mashin. – M.: Mashinostroenie, 1977.
9. Tsymbal A.G. Issledovanie nekotorykh fiziko-mekhanicheskikh svoistv predkavkazskogo chernozema kak osnovy dlya rascheta pochvoob¬ra¬batyva-yushchikh rabochikh organov: Avtoref. dis ... kand. tekhn. nauk. – Volgograd, 1967. – 26 s.
10. Zelenin A.N. Osnovy razrusheniya gruntov mekhanicheskimi sposobami. 2-e izd. – M.: Mashinostroenie, 1968. – 375 s.
11. Vetrov Yu.A. Mashiny dlya zemlyanykh rabot. – Kiev, 1981.
12. Revut I.B. Fizika pochv. L., 1972.
13. Balovnev V.I. Modelirovanie protsessov vzaimodeistviya so sredoi rabochikh organov dorozhno-stroitel'nykh mashin. – M.: Vyssh. shk., 1981. – 335 s.
| 















 This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

