
- About

- Journals

- Authors

- Agreements

- Reviewing

- Advertisement

- Services









|
Library
|
Your profile |
 This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.|
Historical informatics
Reference:
Frolov A.
Evaluation of Coordinate Points Consistency in Medieval Geographical Manuscripts (the case of Ibn Sa'id's Data on the Southern and Eastern Mediterranean)
// Historical informatics.
2021. № 3.
P. 124-143.
DOI: 10.7256/2585-7797.2021.3.36578 URL: https://en.nbpublish.com/library_read_article.php?id=36578
Evaluation of Coordinate Points Consistency in Medieval Geographical Manuscripts (the case of Ibn Sa'id's Data on the Southern and Eastern Mediterranean)
DOI: 10.7256/2585-7797.2021.3.36578Received: 30-09-2021Published: 07-10-2021Abstract: The article develops a technique for analyzing mathematical data (longitude and latitude) characterizing the location of cities in medieval Arabic geographical manuscripts. The calculations made at the coordinates of 19 points given by the Arab-Spanish traveler of the 13th century Ibn Sa'id. These data are taken from his text and from the book of Abu-l-Fida referring to Ibn Sa'id. With the help of the Python - PostgreSQL technological stack for each pair of cities a set of spheroids was determined that fit for placement them in the corresponding coordinates. Then the options for intersecting the sets in all possible combinations are analyzed. The consistent exclusion of all possible combinations of cities from the entire set allows these cities to be arranged according to the degree of consistency of coordinates for any number of withdrawn points. The results tell us that most of the coordinates were not the result of astronomical observations. One of the tasks was to test a hypothesis that some of the cities the coordinates of which were determined more accurately served as “reference” points serving the basis for calculating coordinates of the rest of the cities. Complete consistency of coordinates was achieved with the exclusion of 14 cities from the set in the first version and 13 cities in the second one. However, the geography of the rest cities in Ibn Sa’id’s version does not support the “reference points” hypothesis. Abu-l-Fida’s version can boast a result that is more close to the hypothes, but to prove it one has to solve the problem of data origin used by Abu-l-Fida to correct coordinates. The technique described can be applied to any other set of coordinates of ancient geographical descriptions to evaluate the degree of their consistency and search for “reference” points. Keywords: medieval arabic geography, historical coordinate systems, earth model, medieval mathematical cartography, Mediterranean coast, Ptolemaic geographical tradition, methods of medieval geography, data consistency analysis, historical modeling, historical geoinformaticsВведение В арабской средневековой географии получила развитие традиция характеризовать положение описываемых объектов (например, городов) через географические координаты, то есть пары значений долготы и широты в градусах и минутах. В работе, специально посвященной систематизации координатных данных из средневековых исламских сочинений, учтено 74 источника, каждый из которых содержит от 2 до 656 пунтов с координатами [1]. Исследователи отмечают, что координаты, указанные одним средневековым автором, часто перекочевывают в сочинения других, что позволило им оценить степень близости между собой различных источников. Правда, в предложенных расчетах используется только совпадение по широте, но не по долготе, что делает выводы менее надежными. Практика указания координат географических пунктов была заимствована, по-видимому, из трудов Клавдия Птолемея, с которыми арабская наука была хорошо знакома, хотя конкретные значения долгот и широт в арабских сочинениях с птолемеевыми не совпадают. Современные исследователи отмечают, что арабские авторы не использовали даже его нулевой меридиан, хоть и декларировали это [2]. «Географии» Птолемея повезло – безбрежная историография исследований этого сочинения включает работы не только об источниках приведенных в нем сведений, но и о методах получения Птолемеем географических координат и о математической основе составленной им карты. Исследователи в основном согласны с тем, что реальных измерений широты и, тем более, долготы на базе астрономических наблюдений в распоряжении географа было крайне мало [3, 4]. Сопоставление координат с данными известных Птолемею авторов и анализ соотношения приводимых им расстояний ведет к выводу, что координаты заимствовались им у предшественников или рассчитывались на основе данных о расстояниях между пунктами. Замеры расстояния при этом могли иметь совершенно разное происхождение (как подробные итинерарии или периплы, так и обобщенные оценки кратчайшего расстояния по прямой с указанием направления по сторонам света) и, соответственно, неодинаковую точность. К тому же результаты вычислений систематически округлялись, а отчасти использовали правила не сферической тригонометрии, а евклидовой планиметрии [3, с. 97–102 и др.]. По-видимому, нечто подобное следует предполагать и для арабской средневековой географии, однако ряды данных в этих источниках значительно короче, чем у Птолемея, а степень их изученности существенно меньше. Современные информационные технологии позволяют использовать значения координат из средневековых арабских сочинений, содержащих элементы математической географии, для характеристики соответствующих источников в разных аспектах. Об успехах этого направления можно судить по историографии трудов Клавдия Птолемея. Здесь развиваются различные подходы к анализу математической основы данных о географических пунктах. Увлекательной задачей является локализация по координатам еще не локализованных городов, для чего с помощью различных алгоритмов моделируется искажение географического пространства, наблюдаемое на карте Птолемея [5, с. 117–118]. Однако, как справедливо отмечает Д. А. Щеглов, все эти методы «могут быть эффективны только в той степени, в какой пространство карты Птолемея может считаться таким же непрерывным и однородным, каким является реальное географическое пространство или пространство современной карты» [5, с. 118]. Между тем, сам исследователь делает важные наблюдения, которые свидетельствуют, что «карта Птолемея имела сложное иерархическое строение, при котором координаты большинства пунктов определялись, скорее всего, не относительно своего ближайшего окружения, но относительно небольшого числа наиболее важных опорных точек. При этом, даже если относительно опорной точки положение каждого отдельного пункта было определено верно, относительно своего ближайшего окружения оно могло сместиться непредсказуемым образом» [5, с. 128]. Одним из первых трудов, где только обозначены перспективы «информационного подхода» к арабским источникам, является упомянутая выше работа Кеннеди. Авторы произвели выборочное сравнение широт арабских источников с современными данными и сделали общие наблюдения о характере наблюдаемых отклонений. Координаты городов из арабских географических сочинений коррелировались с современными и позднее [6, 7, 2]. Однако мало пока разработан вопрос об основных параметрах той модели поверхности Земли, при которых могли существовать города с приводимыми в средневековых сочинениях координатами. Одной из причин этого является, вероятно, основанное на изучении конкретных источников предположение о том, что координаты редко опирались на астрономические наблюдения, а потому неточны, а чаще всего еще и являются результатом компиляции из трудов предшественников. Но даже в этом случае вопрос об основных параметрах модели не теряет смысла, поскольку позволяет достаточно определенно судить о согласованности между собой координат различных пунктов в рамках одной географической системы, дает основания для идентификации нелокализованных топонимов на основе значений приведенных для них координат. Поиск подходов к его решению имеет и методическое значение для подбора способов применения информационных технологий к продуктам гуманитарного знания, какими являются исторические источники древности и средневековья. Определение положения в пространстве через градусы и минуты исходит из представления о шарообразной форме Земли, развивавшегося и в европейской дохристианской (Эратосфен, Гиппарх, Посидоний, Марин Тирский, Птолемей и др.), и в арабской традициях (аль-Баттани, Ибн Русте, ал-Хорезми, ал-Бируни и др.). Это, однако, не означает, что градусы широты и долготы рассчитывались на сфере – поверхности шара. Сфера является лишь частным случаем эллипсоида. В трехмерном пространстве параметры эллипсоида задаются размером трех взаимно перпендикулярных полуосей-радиусов, а сферой он называется, если все три его полуоси равны. Поскольку планета вращается вокруг своей полярной оси, ее идеализированная поверхность в современной картографии описывается эллипсоидом вращения (сфероидом), у которого две из трех полуосей равны. По этой причине для расчетов на земном эллипсоиде достаточно знать лишь два параметра: либо длины экваториальной и полярной («большой» и «малой» соответственно) полуосей, либо длину большой полуоси и коэффициент сжатия, отражающий соотношение двух полуосей. У нас нет веских оснований считать, что координаты городов в античных и средневековых географических сочинениях также соответствуют модели на сфероиде, а не на эллипсоиде с неравными друг другу полуосями, лежащими в плоскости экватора, тем более что и идея о вращении Земли вокруг своей оси в рамках геоцентрической парадигмы устройства Вселенной точно не владела умами большинства ученых той исторической эпохи. Известно, что Птолемей считал Землю неподвижной. В перспективе, возможно, следует учесть это обстоятельство, рассмотрев модели из параметров трех полуосей. Однако в настоящей работе мы будем исходить из допущения о том, что «арабские координаты» находятся на сфероиде, поскольку главной ее задачей является апробация базовой методики моделирования параметров Земли по координатам исторических источников и проверка согласованности этих координат.
Источники и подходы Одним из значительных памятников арабской научной литературы является сочинение эмира сирийского города Хама Абу-л-Фиды «Таквим ал-булдан» («Упорядочение стран», 1321–1331 гг.). По популярности в рейтинге арабских сочинений, известных в Западной Европе, оно уступало только Корану и «1001 ночи» [8, с. 392]. На русском языке изданы фрагменты сочинения, касающиеся Восточной Европы (перевод И. Г. Коноваловой и характеристику источника см.: [9]). Труд Абу-л-Фиды был компилятивным и объединял сведения различных источников, некоторые из которых ученый указывал. Особенно важно это в контексте рассматриваемой темы потому, что позволяет ограничить круг данных (в первую очередь – пар географических координат городов), могущих находиться в соответствии друг другу. Наиболее многочисленны данные, заимствованные Абу-л-Фидой у Ибн Са'ида – арабо-испанского путешественника XIII в. [9]. Анализ данных о широтах городов южного и восточного побережий Средиземного моря у Ибн Са'ида через сравнение разницы в «арабских» градусах и минутах с реальным расстоянием между соответствующими пунктами в метрах и перебором различных вариантов «арабского азимута» (перемена которого влечет за собой изменение и длины одного «арабского» градуса широты) позволяет заключить, что величина градуса широты из сочинения Ибн Са'ида не опиралась на астрономические расчеты. При этом размеры соответствующего полярного радиуса Земли (то есть «малая полуось»), независимо от того, как эти широты вычислялись, были несколько переоценены относительно действительных [10]. Оценка размеров «арабского» градуса долготы представляет собой значительно более сложную задачу. Если расстояние между параллелями неизменно и почти не зависит от близости к экватору или полюсу, градус долготы имеет максимальную длину на экваторе и плавно сводится к нулю на полюсах. Поэтому, рассчитав расстояние между двумя точками, лежащими на одной «арабской» параллели, мы не можем судить о расстоянии между двумя другими точками, лежащими на другой параллели, даже будучи уверены в том, что обе пары точек получили свои координаты на одном и том же сфероиде (с неизвестными размерами полуосей). А поскольку последнее как раз и следует проверить в первую очередь, изучение разницы по долготе само по себе не может быть отправной точкой исследования. Однако средства геоинформатики позволяют подойти к этой проблеме с противоположной стороны: рассчитать диапазоны параметров сфероида, подходящих для описания положения на нем известных городов. Если взять отдельно пару координат одного города, она может быть локализована на сфероиде абсолютно любого размера, поскольку любой сфероид может быть покрыт градусной сеткой, где всегда отыщется нужное значение в диапазоне от -180 до 180. Выделение диапазона подходящих параметров сфероида возможно по любой паре точек с известными координатами, где критерием для отбора будет служить близость расстояния между этими точками на данном сфероиде к реальному расстоянию, измеренному на эллипсоиде, лежащем в основе современной системы геоцентрических координат WGS84. Нахождение расстояния между двумя точками с известными географическими координатами называется «обратной геодезической задачей», решение которой возможно стандартными средствами любого ГИС-приложения. Оно, однако, в нашем случае осложнено тем, что выполняется для множества комбинаций параметров сфероида, не совпадающих с параметрами земного эллипсоида. По этой причине для каждой пары городов подходящим будет являться целое множество сфероидов. Смысл всей этой процедуры заключается в определении параметров полуосей сфероидов, подходящих максимальному количеству пар городов. Программными средствами для решения этой задачи послужили процедурный язык Python (v. 3.6) с набором библиотек (numpy, itertools, multiprocessing и др.), СУБД PostgreSQL (v. 12) с модулем для обработки геоданных PostGIS (v. 2.5.2.), для визуализации полученных результатов использована QGIS (v. 3.16). Анализ данных о широтах городов южного и восточного побережий Средиземного моря у Ибн Са'ида позволил очень примерно определить те значения, в пределах которых могла колебаться длина одного градуса его широты [Фролов]. Имея в виду эти результаты, диапазон длин полуосей был взят со значительным запасом: длины малой полуоси сфероида рассматривались в диапазоне от 5500000 до 7500000 метров (при равенстве действительного значения 6 356 752 м – WGS84). В еще большем спектре рассмотрены возможные длины большой полуоси – от 4500000 до 7500000 метров (при равенстве действительного значения 6 378 137 м – WGS84). Значения из этих диапазонов с шагом в 10000 м образуют декартово произведение (300 x 200), элементами которого являются все возможные сочетания длин большой и малой полуосей. На полученных таким образом 60000 сфероидах в координатах Ибн Са'ида (преобразованных в десятичные градусы, с которыми работает PostGIS) попарно размещались города. Всего имеются сведения о координатах 19 городов, которые образуют 171 комбинацию (дубли типа A-B и B-A обрабатывались как одна комбинация, пары типа А-А исключены, поскольку смысла не имеют). Обработка геоданных (в данном случае – расчет расстояний на сфероиде между городами каждой пары) возможна как непосредственно в коде скрипта Python, так и средствами СУБД. Оба решения имеют плюсы и минусы. Первое решение обычно считается предпочтительным в связи с тем, что обращение к клиент-серверной БД сопряжено с накладными расходами, особенно высокими при размещении БД на удаленном сервере, взаимодействие с которым требует соединения по сети интернет. Для настоящего исследования БД была размещена сначала на локальном хосте, так что для манипуляций с несколькими миллионами записей подошло и второе решение. Анализ данных выполнялся путем SQL-запроса из скрипта Python к базе данных и обработки его инструментами СУБД. Такое решение более удобно и для визуализации в среде QGIS, поскольку любые эксперименты с исходными данными, оформленные в СУБД в виде отдельного представления (view), легко подгружаются в виде PostGIS-слоя прямо в картографическое приложение. К сожалению, несколько позже пришлось столкнуться и с минусами – когда по мере реализации плана возникла идея провести дополнительные расчеты над данными БД. Поскольку PostGIS для расчетов на сфероиде принимает в качестве параметров длину большой полуоси и коэффициент полярного сжатия, этот коэффициент предварительно вычислялся и хранился в памяти компьютера в виде отдельного объекта-матрицы, соответствующие элементы которой подставлялись в SQL-запрос.
Анализ координат Ибн Са'ида В сочинении Абу-л-Фиды на южном и восточном берегах Средиземного моря со ссылкой на Ибн Са'ида приведены координаты 19 городов: Танжер, Сеута, Беджая, Буна, Бизерта, Тунис, Сус, Махдия, Сфакс, Триполи Западный, Сирт, Толмейта, Александрия, Рашид, Думьят, Газа, Ашкелон, Акко, Бейрут (здесь они приведены по ходу движения вдоль берега с запада на восток (рис. 1)). Однако необходимо заметить, что для шести из них (Ашкелон, Беджая, Бизерта, Газа, Рашид, Сфакс) координаты в сохранившемся тексте Ибн Са'ида несколько отличаются от тех, что указаны Абу-л-Фидой со ссылкой на Ибн Са'ида [Kennedy]. Не имея возможности определенно судить о причинах появления у Абу-л-Фиды своей версии координат Ибн Са'ида (использование в качестве протографа несохранившегося списка, ошибка прочтения, корректировка по собственной инициативе т. д.), мы рассмотрим обе версии координат.
Рис. 1. Города южного и восточного Средиземноморья, для которых известны координаты по Ибн Са'иду.
Для каждой из 171 комбинаций пар городов создавалась двумерная матрица, хранящая результаты измерения расстояний на одном из 60000 сфероидов. Вычитание из нее матрицы того же размера с расстояниями на земном эллипсоиде WGS84 позволяет вычислить величину расхождения между ними. Однако сама по себе эта величина малоинформативна, поскольку разброс реальных расстояний слишком велик (от 32 км (Газа – Ашкелон) до 3757 км (Танжер – Бейрут)). Поэтому «коэффициент расхождения» измеренной длины с расстоянием на эллипсоиде WGS84, записанный в итоговую матрицу, рассчитывался как доля, которую составляет величина расхождения от реального расстояния, взятая по модулю. Таким образом было получено 171 множество, в каждом из которых 60000 элементов хранили «коэффициент расхождения» «арабских» расстояний от реальных на одном из вариантов сфероида. Фактически каждый элемент такого множества является оценкой того, насколько те или иные параметры сфероида подходят для расположения соответствующих двух городов в координатах Ибн Са'ида, чтобы расстояние между ними соответствовало действительному. При этом точное соответствие ожидать невозможно, поскольку в средневековых географических сочинениях координаты приводятся с точностью до минуты, а следовательно, только инструментальная погрешность измерения составляет около километра (длина одной минуты земного меридиана составляет около 1852 м, а размер инструментальной погрешности принимается за половину деления прибора, то есть в данном случае половину одного деления градусной шкалы). Остальные погрешности, учитываемые в метрологии (метода, модели, оператора), оценить невозможно, поскольку у нас нет никаких сведений о способах получения этих координат. Для определения порогового значения «коэффициента расхождения», превышение которого исключает эллипсоид из числа рассматриваемых, важно представлять распределение минимальных значений этого коэффициента среди 171 множества, то есть того, как близко к реальным расстояниям может приблизиться результат измерения расстояния между парой городов на самом подходящем сфероиде множества. Чрезмерно строгий фильтр отбросит слишком много пар городов, в том числе и те, координаты которых могли находиться на том или ином сфероиде, но были вычислены недостаточно точно. В результате небольшое количество пар городов, для которых подходят параметры того или иного сфероида, не смогут наглядно продемонстрировать закономерность попадания на один сфероид нескольких множеств, даже если такая закономерность существует. Недостаточно строгий фильтр, наоборот, позволит выделить большее количество пар городов, попадающих на один сфероид, однако они значительно менее адекватно будут характеризовать связность координат городов, входящих в пару. Для анализа распределения минимальных значений в 171 множестве была произведена кластеризация, при которой среднее отклонение каждого класса от среднего значения класса сводится к минимуму при максимальном отклонении каждого класса от среднего значения других классов. Это задача статистическая, она не требует использования пространственных данных, однако современные картографические приложения тоже оснащены таким инструментарием. В QGIS эта процедура над табличными данными носит название классификации естественных границ (по Дженксу), применяемая при оформлении палитры объектов с помощью градуированных знаков. Рассмотрим сначала вариант координат, который содержался непосредственно в сочинении Ибн Са'ида. Из 171 множества в 137 (более 80%) минимальные значения расхождений с реальным расстоянием не превышают 8,61%. Минимумы в остальных множествах больше этого порога, что трудно уже объяснить погрешностями измерения (рис. 2), поэтому они были исключены из анализа. Таким образом, в выборку попали 137 множеств (пар городов), для которых подходящими параметрами сфероида были признаны только те, которые при измерении расстояния между городами в «арабских» координатах дают результат, отличающийся от промеров на земном эллипсоиде не более чем на 8,61%. Таких вариантов нашлось 1 851 187. 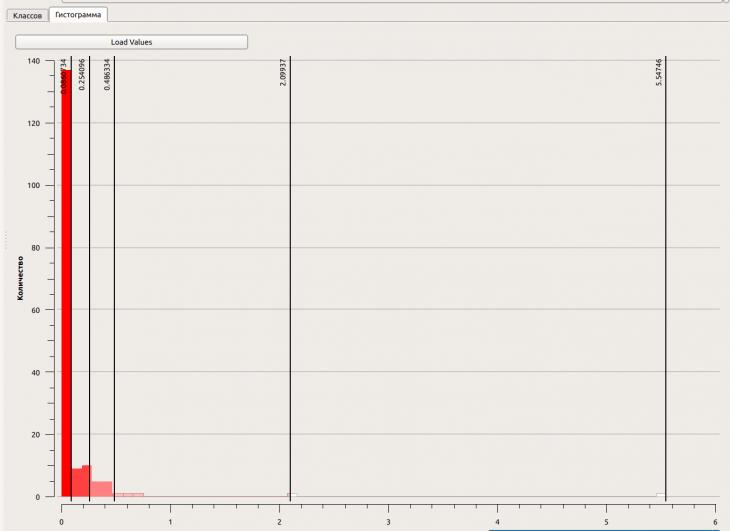 Рис. 2. Распределение минимальных отклонений от реальных расстояний между парами городов в 171 множестве.
Группировка отобранных для анализа данных с помощью SQL-запроса была выполнена следующим образом. Шаг 1. Для каждого из 60000 сфероидов в таблице были агрегированы все комбинации пар городов, которым данный сфероид подходит по параметрам. Тем самым все возможные комбинации различной длины из пар городов, которые могут быть отображены в «арабских» координатах на одном сфероиде, оказались собраны в одной записи. Шаг 2. Агрегация производилась в обратную сторону – для каждой из комбинаций пар городов агрегировались параметры подходящих сфероидов. То есть все сфероиды, которые подходят для конкретной комбинации пар городов, были собраны в одной записи. Общим результатом стало выделение 1181 группы, внутри которых одной комбинации пар городов подходит один и тот же набор сфероидов. Надо сказать, что при установленном выше фильтрующем значении «коэффициента расхождения» совпадения параметров сфероидов для множества пар городов — довольно частая вещь. Параметры любого сфероида из обозначенного диапазона подходят как минимум для 16 пар городов. Однако максимум значительно больше — в одной группе из 43 пар городов насчитывается 3 общих сфероида. В качестве простого критерия, который позволяет оценить удаленность модели от эталонной (в которой координаты действительно согласованы), может служить то, насколько количество пар городов в самой многочисленной группе отличается от общего числа комбинаций. Для эталона «коэффициент согласованности» равен 1 (общие сфероиды имеет 171 пара городов из 171 возможных). В случае с координатами Ибн Са'ида он составил 43/171=0,2515. В целом это означает, что наборы координат всех 19-ти городов южного Средиземноморья, описанных у Ибн Са'ида, не находятся в некой согласованной системе, позволяющей найти пересечение всех множеств хотя бы на одном сфероиде. Попробуем теперь рассчитать другую версию координат Ибн Са'ида, которая приведена в сочинении Абу-л-Фиды. Для сопоставимости в качестве фильтрующего порога было взято то же значение 8,61%. При нем в таблице оказалось 1887914 записей, характеризующих 139 вариантов пар городов. На шаге 1 остались все 60000 сфероидов, а на шаге 2 они оказались сгруппированы по 1133 комбинациям пар городов. «Коэффициент согласованности» составил 45/171=0,2632. Это чуть больше, чем в первом варианте, что едва ли может быть уверенно интерпретировано как улучшение первоначальных данных Абу-л-Фидой, поскольку разница слишком незначительна. Распределение параметров сфероида по выделенным группам для координат по Ибн Са'иду в обоих вариантах удобно отобразить с помощью QGIS в собственной системе координат, представив параметры экваториальной полуоси как координату X, а полярной полуоси как Y (рис. 3, 4). Для того, чтобы легче было ориентироваться на ней, полезно указать место в этой системе координат параметров WGS84 (красная звездочка), а также диагональю (пунктирная линия) обозначить множество, где длина экваториальной полуоси равна длине полярной – то есть сфероид является сферой («диагональ параметров сферы»). Ниже этой диагонали лежат все сфероиды, у которых соотношение полуосей сходно с действительным (экваториальная полуось больше полярной), а выше нее – сфероиды-антиподы, полярная ось у них превышает экваториальную. В целом для обеих версий координат средиземноморских городов полученная «картинка» может быть охарактеризована как «лоскутное одеяло». На нем хаотично чередуются группы сфероидов, выделенные по принадлежности к одной комбинации пар городов, где параметры сфероидов являются подходящими для размещения в координатах Ибн Са'ида.
Рис. 3. Группировка сфероидов по принадлежности к одной комбинации пар городов, где параметры сфероидов являются подходящими для размещения в координатах Ибн Са'ида (без поправок Абу-л-Фиды).
Рис. 4. Группировка сфероидов по принадлежности к одной комбинации пар городов, где параметры сфероидов являются подходящими для размещения в координатах Ибн Са'ида (с поправками Абу-л-Фиды).
Для того, чтобы представлять, как выглядит распределение в согласованных координатах, аналогичные процедуры были выполнены для тех же городов в реальных координатах, приложенных к тому же диапазону сфероидов. При том же пороге в 8,61% количество подходящих сфероидов составило 3582603. На первом шаге процедуры было получено 52051 записей (каждая соответствует отдельному сфероиду), на втором 1524 комбинаций пар городов. По эталонному варианту можно определить ряд топологических черт, указывающих на согласованность координат рассматриваемого набора пунктов (рис. 5).
Рис. 5. Эталонная группировка сфероидов по принадлежности к одной комбинации пар городов, где параметры сфероидов являются подходящими для размещения в современных координатах (отклонение от реальных расстояний между городами не превышает 8,61%).
1. Только один набор сфероидов является «полным», подходящим сразу для всех 171 комбинации пар городов. 2. Сфероид с параметрами WGS84 совпадает с местонахождением центроида этого набора. 3. Именно этот набор объединяет самое большое количество сфероидов, которое значительно превышает любой другой набор, подходящий для меньшего числа комбинаций пар (8907, следующий по численности набор – 4487 сфероидов. Здесь точное количество значения не имеет, поскольку часть вариантов оказалась обрезана избранным диапазоном значений сфероида). 4. Число пар городов, которым подходит сфероид в «неполных» наборах, плавно убывает по мере удаления от «полного» набора. Центром симметрии при этом оказывается сфероид WGS84. 5. Один и тот же «неполный» набор пар городов располагает двумя массивами подходящих сфероидов по разные стороны от «диагонали параметров сферы» (рис. 6). Это объясняется тем, что одно и то же расстояние между пунктами можно получить на сфероидах двух разных видов, различаемых по соотношению экваториальной и полярной полуосей. 6. Распределение комбинаций пар городов вокруг параметров сфероида WGS84 является нормальным. Рис. 6. Симметричное расположение пар массивов подходящих сфероидов (показаны красным цветом) по разные стороны от «диагонали параметров сферы» на эталонной модели.
Представление распределения комбинаций пар городов в виде трехмерной модели, где высота демонстрирует число пар в соответствующей комбинации, наиболее наглядно (рис. 7, 8).
Рис. 7. Трехмерное представление распределения комбинаций пар городов на эталонной модели (высота демонстрирует число пар в соответствующей комбинации).
Рис. 8. Трехмерное представление распределения комбинаций пар городов с координатами Ибн Са'ида без поправок Абу-л-Фиды (высота демонстрирует число пар в соответствующей комбинации).
Очевидная пропасть между любым из вариантов координат Ибн Са'ида и эталоном, на мой взгляд, делает возможными три варианта интерпретации: 1) координаты городов, приведенные Ибн Са'идом, вовсе не соотносятся с расчетами на сфероиде; 2) для разных групп городов подходят разные сфероиды; 3) для части городов верно первое утверждение, для другой возможно обнаружить соответствие их координат параметрам одного или нескольких сфероидов. В частности, такое возможно, если при расчете координат большинства городов в качестве опорных точек использовались более точные данные о положении нескольких, служащих своего рода «реперами». Попробуем проверить, насколько вероятна эта гипотеза.
Поиск набора городов с согласованными координатами До сих пор мы работали с выборкой пар городов, откуда были удалены такие пары, взаимное расстояние в которых не может приблизиться к действительному ни на одном из 60000 сфероидов выбранного диапазона без предположения об ошибке, превышающей размер «коэффициента расхождения». Однако такая фильтрация данных является довольно грубой, поскольку ошибочное указание координаты одного пункта не может влиять на искажение удаленности до других пунктов выборочно, а влияет на согласованность координат всей совокупности. Следовательно, для оценки того, насколько участие того или иного города в совокупности удаляет ее от эталона, этот город нужно исключить из нее и «пересобрать» соответствующим образом все комбинации оставшихся пар по обозначенным выше шагам 1 и 2. Наименее согласованными окажутся координаты того города, чье изъятие дало «коэффициент согласованности», максимально приближенный к 1. Задача здесь несложная – при наличии 19 городов она требует выполнить 19 запросов к БД. Очевидно, однако, что чем больше городов мы попытаемся исключить, тем ближе максимальный коэффициент окажется к эталону, а количество необходимых для этого запросов к БД определяется числами в 19-м ряду «пирамиды Паскаля»: 19, 171, 969, 3876, 11628, 27132, 50388, 75582, 92378 и обратно до 19. Для расчета максимального «коэффициента согласованности» и выбора соответствующих комбинаций городов с любым количеством исключаемых пунктов необходимо, таким образом, сделать 524286 запросов к БД минус последние 190 (171+19), поскольку расчеты «коэффициента согласованности» при изъятии более чем 16 из 19 пунктов смысла не имеют. Здесь проявляются минусы реализации вычислений через СУБД, поскольку, как отмечалось, наибольшие накладные расходы связаны как раз с затратами на отправку запроса и получение ответа от БД. Временные затраты на один запрос (достаточно сложный) к СУБД, развернутой на машине с процессором Intel(R) Core(TM) i9-9980HK CPU @ 2.40GHz, в штатном режиме составляют более 4 секунд, а все расчеты требуют месяца машинного времени. Это заставило искать способы ускорения. Возможным направлением является поиск альтернативы для реляционной СУБД, поскольку доступ к данным, хранимым в виде пары «ключ — значение», сам по себе является более скоростным, а размещение БД в оперативной памяти (например, СУБД Redis) еще более увеличивает производительность. Однако смена архитектуры СУБД требует полной замены структуры и содержания запроса к БД, а PostgreSQL все же кажется более удобной для дальнейшей работы с ГИС, поэтому решено было не отказываться от нее. Сильной стороной ее клиент-серверной архитектуры является обеспечение конкурентного доступа к БД, при котором к одним и тем же данным может обращаться одновременно множество сеансов. Благодаря механизму изоляции транзакций PostgreSQL позволяет избежать блокировок доступа одного сеанса при обслуживании другого. Чтобы воспользоваться этим для решения нашей задачи, необходимо реализовать многопоточную обработку кода интерпретатором Python. Ведь код скрипта выполняется построчно, так что даже современный многоядерный процессор в один момент времени обычно использует для выполнения кода только одно ядро. В этом легко убедиться, воспользовавшись одной из утилит мониторинга операционной системы. Специальные библиотеки Python, однако, обеспечивают в рамках программного кода создание такого количества потоков, одновременная обработка которого физически обеспечена числом ядер процессора, так что тот же восьмиядерный процессор ноутбука сможет выполнять код в 8 раз быстрее, создав не 1, а 8 сеансов работы с СУБД – каждый сеанс в отдельном потоке. Еще более радикальное решение, которое в результате и было применено, – это развертывание виртуальной машины с БД в «облаке» и использование вычислительных мощностей 32-ядерного процессора (и это не предел возможностей современных коммерческих облачных платформ).
Заключение В результате проведенных вычислений выявлены максимальные значения «коэффициента согласованности» и соответствующие им комбинации городов в двух вариантах координат Ибн Са'ида – при изъятии из выборки от 1 до 16 пунктов. Это позволяет охарактеризовать согласованность координат средиземноморских городов следующим образом. Вариант координат без корректировок Абу-л-Фиды: изъятие из выборки менее чем 14 городов не позволяет достичь согласованности координат ни при каких комбинациях. При изъятии 14 городов возможны 4 варианта, в которых неизменно оказались города Танжер, Сеута, Беджая, Буна, Бизерта, Тунис, Сус, Сирт, Газа, Акко, Бейрут. Вариативность связана с тем, что результат достигается при изъятии еще любых трех из следующих городов: Александрия, Рашид, Думьят, Ашкелон. Хорошо согласованными координатами обладают, таким образом, Махдия, Сфакс, Триполи Западный, Толмейта и один из четырех городов юго-восточного участка побережья: Александрия, Рашид, Думьят, Ашкелон. Однако географическое положение этих городов не дает уверенности в том, что они могли служить своеобразными «реперами» для расчета координат окружающих пунктов. Если из четырех городов юго-восточного побережья оставить Александрию, то получится, что согласованные по координатам города располагаются друг за другом (рис. 1). Только Сирт находится между Триполи и Толмейтой. В этом случае полученный результат с большей вероятностью лишь свидетельствует, что измерения положения городов на центральном отрезке южного берега Средиземного моря отличались качественно от остальных. Если же из четырех городов предпочесть, например, Ашкелон, то идея о «реперных» точках получит чуть больше оснований. Таким образом, проведенные расчеты не подтверждают явным образом предположение об использовании при расчете координат городов, указанных Ибн Са'идом, некой «реперной» сети из пунктов, для которых координаты рассчитаны точно, относительно которой вычислялись координаты других городов. Вариант координат с корректировками Абу-л-Фиды: для достижения согласованности координат оказалось достаточным изъять 13 городов, причем расчеты дали лишь одну комбинацию таких пунктов, что упрощает интерпретацию результата. Согласованы между собой по координатам 6 городов: Махдия, Сфакс, Триполи Западный, Толмейта, Думьят, Ашкелон. Ссылаясь на Ибн Са'ида, Абу-л-Фида скорректировал его координаты таким образом, что сделал более соответствующим общей системе положение городов юго-восточного Средиземноморья. Этот вывод требует осмысления, потому что специальный анализ того, широта каких городов из того же списка наименее согласована с остальными, предпринятый ранее [10,с. 335–337], как раз города Махдия, Сфакс и Триполи Западный выделил в тройку лидеров. В целом география согласованных между собой по координатам городов теперь больше соответствует гипотезе о «реперных точках», однако каким образом это может быть интерпретировано, зависит от происхождения данных, внесенных Абу-л-Фидой. Если они были взяты из неизвестной редакции сочинения Ибн Са'ида, то проведенные расчеты подкрепляют эту гипотезу. Если же мы имеем дело с «точечными» корректировками самого Абу-л-Фиды, то первоначальные способы определения координат в системе Ибн Са'ида это никак не характеризует. Построение модели распределения комбинаций для оставшихся 6 городов по версии Абу-л-Фиды (рис. 9, 10) свидетельствует, что в ней достигнута симметрия «неполных наборов» сфероидов относительно единственного «полного», подходящего для всех пар городов.
Рис. 9. Группировка сфероидов по принадлежности к одной комбинации пар из 6 городов, координаты которых (с поправками Абу-л-Фиды) являются согласованными.
Рис. 10. Трехмерное представление распределения комбинаций пар из 6 городов, координаты которых (с поправками Абу-л-Фиды) являются согласованными (высота демонстрирует число пар в соответствующей комбинации).
Правда, «полный набор», в отличие от эталонного, один из самых малочисленных по количеству сфероидов и почти не выделяется среди «неполных» в рельефе. Кроме того, «рисунок» распределения этих наборов отличается от эталонного примитивностью (ср. рис. 5). Для объяснения причин этих отличий необходим, видимо, дальнейший анализ материала. Описанная методика, независимо от результатов, полученных при изучении координат Ибн Са'ида, может быть использована для анализа согласованности координат любых других географических сочинений древности и средневековья.
References
1. Kennedy E. S., Kennedy M. H. Geographical coordinates of localities from Islamic sources. Frankfurt-am-Main, 1987, 723 p.
2. Mercier E. Meridians of reference and mathematical geography in the Medieval Muslim West (9th-16th centuries) // e-Perimetron, Vol. 15, № 2, 2020, p. 98–113. 3. Shcheglov D. A. Predystoriya geografii Ptolemeya // Aristei. Vestnik klassicheskoi filologii i antichnoi istorii. T. X. M., 2014. S. 82–131. 4. Grasshoff G. Ptolemy and Empirical Data // Astroculture. Figurations of Cosmology in Media and Arts. München, 2014, p. 32–44. 5. Shcheglov A. D. Stroenie prostranstva v «Geografii» Ptolemeya: metodologicheskie slozhnosti georeferentsirovaniya antichnykh toponimov // Scholae. Filosofskoe antikovedenie i klassicheskaya traditsiya, 13 (1), 2019. S. 115–136. 6. Sezgin F. Mathematical Geography and Cartography in Islam and their Continuation in the Occident, 3 vols., Geschichte des Arabischen Schrifttums. Frankfurt am Main, 2005. 7. Robles Macías L. A. The longitude of the Mediterranean throughout history: facts, myths and surprises // e-Perimetron, Vol. 9, № 1, 2014, p. 1–29. 8. Krachkovskii I.Yu. Izbrannye sochineniya. T. IV. M.; L., 1957. 919 s. 9. Konovalova I. G. Vostochnaya Evropa v sochineniyakh arabskikh geografov XIII–XIV vv. – M., 2009. 223 s. 10. Frolov A. A. Otsenka sredstvami geoinformatiki parametrov koordinatnoi sistemy arabskikh geografov XIII – XIV vv. Abu-l-Fidy i Ibn Sa‘ida o poberezh'e Sredizemnogo morya // «Istoricheskie issledovaniya v kontekste nauki o dannykh: informatsionnye resursy, analiticheskie metody i tsifrovye tekhnologii». Materialy mezhdunarodnoi konferentsii. Moskva, 4-6 dekabrya 2020 g. M., 2020. S. 329–339 |


