To Count the Absent (or the Problem of the Total Number of Genoese Merchants in Byzantium)

I. Введение

Одной из интересных и захватывающих тем в исторических исследованиях является математическое, формализованное оценивание какого-либо неизвестного показателя по косвенным данным массовых источников. В частности, проблеме реконструкции численности генуэзской торговой общины в Византии посвящен ряд работ яркого, талантливого, но, к сожалению, рано ушедшего от нас историка Андрея Леонидовича Пономарева. Настоящая статья, можно сказать, подхватывает эту проблематику и предлагает для решения этой задачи использовать развитый математический аппарат статистического оценивания.

Вдохновленные Нимфейским договором 1261 года, генуэзцы, а если брать шире – жители Лигурийского побережья, развили уже к началу 1280-х годов в Византии бурную коммерческую деятельность, о чем красноречиво свидетельствуют многочисленные акты о торговых товариществах, наймах судов, завещаний, купли и продажи домов, товаров и людей. Один отрывок из хроники Никифора Григоры, относящийся, правда, к несколько более позднему времени, дает представление о масштабах деятельности генуэзской торговой общины: “их ежегодный доход от пошлин обратился, примерно, в 200 тысяч, а у византийцев он с трудом доходил до 30 тысяч”^[1]. Вместе с тем ни один источник не говорит хотя бы приблизительно о численности этой общины. В связи с этой задачей А.Л. Пономарев привлекает опубликованные Г. Брэтиану в 1927 году акты в той их части, которые были составлены в 1281 году Габриэлем де Предоно, нотарием города Пера – генуэзской колонии напротив Константинополя ^[2].

Необходимо отметить, что далеко не все генуэзцы в Пере являлись клиентами Предоно. А те персоналии, которые упоминались в его актах, могли заключать сделки и у других нотариев. Несмотря на такую непростую картину, А.Л. Пономарев показывает как, зная частоты упоминания клиентов Предоно, можно оценить приблизительную численность клиентелы всех генуэских нотариев в Пере ^[3].

Для решения этой задачи реконструкции А.Л. Пономарев сначала строит формализованную вероятностную модель, описывающую поведение генуэзских купцов при заключении сделок и посещении нотария. Так, ученый представляет это как цепной процесс, в котором совершение очередной сделки у данного нотария обусловлено успешным совершением предыдущей у того же нотария. Другими словами, чем больше купец заключил сделок, тем больше вероятность что он заключит ее еще раз.

Учет указанных феноменов “успеха” и “склонности” А.Л. Пономарев проводит с помощью комбинации двух отрицательных биномиальных распределений ^{[4, с.171-174]}, что позволяет получить формулу частоты упоминания различных персоналий в нотариальных актах Предоно. Отсюда ученый определяет и число персоналий, либо не упомянутых в его актах, либо совершавших сделки у других нотариев, либо вообще их не посещавших (общее число генуэзцев в Пере как 1786 против 507, упомянутых у Предоно). В то же время А.Л. Пономарев указывает и на недостаток предложенного подхода, заключающийся в необходимости учета дополнительного параметра–прогнозируемого числа генуэзцев, который строго не определяется.

В последующей своей статье ученый для описания зависимости между количеством упоминаний и числом купцов, отмеченных не менее, чем указанное число раз, предлагает использовать закон Ципфа, который весьма часто используется для анализа ранжированных рядов (например, частоты цитирования работ различных авторов) ^[5]. А.Л. Пономарев расширяет этот закон и на случай нулевого числа упоминаний, что приводит ученого к пересмотру прежней оценки численности купцов (645-650 человек).

Вместе с тем А.Л. Пономарев указывает и на один важный недостаток предложенного подхода – параметры закона Ципфа не имеют качественного наполнения, отчего этот закон описывает совокупность данных, но не объясняет их структуру. Для устранения этих недостатков при реконструкции общей численности автор настоящей статьи предлагает использовать новый подход, основанный на применении математического аппарата статистического оценивания.

II. Неформальное введение в статистическое оценивание объема конечной совокупности

Обозначим через N – число элементов (объем) генеральной совокупности, а через n – число элементов ее выборки. Будем считать (и это существенно!), что элементы попадают в выборку случайным образом, а затем возвращаются обратно в генеральную совокупность. Такая выборка называется выборкой с возвращением. То есть один и тот же элемент может встречаться в выборке несколько раз.

Интуитивно понятно, что чем чаще встречаются элементы в случайной выборке, чем меньше в ней число i различных элементов, тем правдоподобней выглядит гипотеза, что объем n выборки соразмерен с объемом N всей генеральной совокупности. На этом, по сути, и основана идея оценивания числа N. В данной статье автор следует подходу, основанному на применении принципа максимального правдоподобия ^[6]. Суть этого принципа состоит в предположении, что вся информация о выборке содержится в функции правдоподобия. В нашем случае эта функция представляет из себя формулу для совместной вероятности выборки, зависящей от N как от своего параметра. Подставляя в эту функцию реальные выборочные данные и максимизируя ее по параметру N, получаем наиболее “правдоподобную”, близкую к реальности величину объема генеральной совокупности.

Итак, исходя из нашего предположения о случайности выборки, вероятности оказаться в ней для каждого элемента генеральной совокупности одинаковы и равны 1/N. Наша задача состоит в оценивании величины N при условии, что число i различных элементов, оказавшихся в выборке объема n, известно. Вероятность того, что в выборке размера n первый элемент из генеральной совокупности содержится n₁раз, второй элемент–n₂ раза, …, последний – n_N раза, носит название полиномиального распределения ^{[4, с.174-175]} и равна

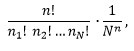
где через n! обозначен факториал числа n: n=n(n-1)(n-2)..2·1, и n = n₁+n₂+..+n_N.

Отсюда вероятность того, что ровно i различных элементов встретятся в выборке размера n равна

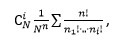
где через С_Nⁱ обозначено число сочетаний из N по i: С_Nⁱ=N!/(i! (N-i)!)), а через Σ – операция суммирования по всем наборам (n₁,..,n_i), таким, что n_j>0 (j=1,2,..,i) и n₁+n₂+..n_i=n, то есть все наборы состоят из положительных чисел, в сумме дающих величину n объема выборки.

Заметим, что в последней формуле от величины N зависят только первые два множителя. Поэтому для решения задачи максимизации функции правдоподобия достаточно ограничиться анализом функции f(N,n,i):

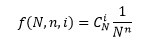
Максимальное значение эта функция в точке N₀ принимает тогда и только тогда, когда выполняются два неравенства:

f(N₀-1,n,i) ≤ f(N₀,n,i) и f(N₀,n,i) ≥ f(N₀+1,n,i),

что эквивалентно выполнению двух неравенств с участием натуральных логарифмов ln:

ln N₀ – ln(N₀-i) ≥ n (ln N₀ – ln(N₀-1)) и ln(N₀+1) - ln(N₀-i+1) ≤ n (ln(N₀+1) - ln N₀).

Обозначив через S(N,i) функцию

,

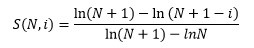мы приходим к более простой записи предыдущих двух условий:

S(N₀,i) ≤ n ≤ S(N₀-1,i).

Отметим, что функция S(N,i) (таблица ее значений частично приведена в Приложении 1) убывает с ростом N при фиксированном i. Поэтому, подставив в последние два неравенства реальные выборочные значения i и n, находим искомую оценку для объема генеральной совокупности как наименьшее значение параметра N, при котором целая часть от S(N,i) не превосходит n: ]S(N,i)[ ≤ n.

III. Численные эксперименты

Апробация предложенного автором подхода была проведена на том же материале, что и у А.Л. Пономарева – 149 актов Предоно, составленных в Пере с июня по октябрь 1281 года. Все они распадаются на несколько типов, наиболее часто встречающимся из которых является договор комменды [7]. Несмотря на однородность формуляра актов, идентификация упомянутых в них некоторых персоналий трудновыполнима. Так, довольно часто в актах упоминаются персоналии без указания фамилий, с одними именами или со схожими именами, как например Ogerius ^{[2, с.89]}, Ogerinus ^{[2, с.91]}. И лишь дополнительное указание их профессии или должности (например, placerius peliparius) позволяет идентифицировать их как одно лицо. К тому же, весьма часто одно и то же лицо выступает в документах в разных ролях. Так, тот же Ogerius в одних договорах комменды выступает в качестве трактатора (accomendatarius, то есть партнера, получающего средства от коммендатора для ведения торговли в установленном месте), в других договорах – в роли свидетеля, а в актах завещания – в роли получателя по завещанию.

Решение подобной задачи идентификации было существенно облегчено созданием автором базы данных на Access (схему данных и структуру таблиц см. Приложение 2). Всего в актах было идентифицировано 447 персоналий, которые были упомянуты 866 раз (сюда включены и женщины). В то же время рабы, как объекты сделок купли/продажи, в рассмотрение не брались. Ниже приведен график частот упоминания отдельных персоналий, упорядоченный по неубыванию.

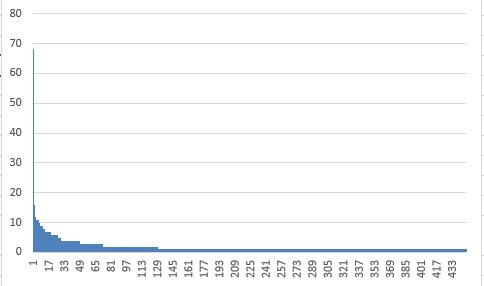
Рис. 1 Ранжированный ряд упоминаний персоналий в актах Предоно 1281 года

Первому рангу (максимальная частота – 68 упоминаний) соответствует одно лицо – нотарий Guglielmo Gandulfi, почти постоянно привлекавшийся в качестве свидетеля договора. Все остальные лица упоминаются существенно меньшее число раз, что приводит к существенной масштабируемости графика на рис.1. Для повышения наглядности ниже приводится тот же график, но без учета этой максимальной частоты:

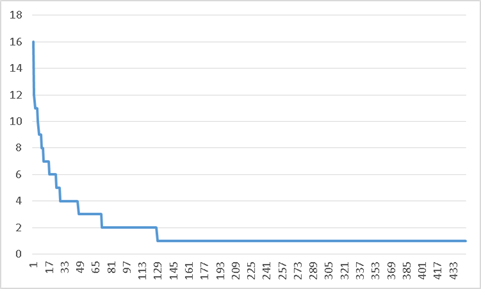
Рис. 2 Ранжированный ряд упоминаний персоналий в актах Предоно 1281 года без первого ранга

Как мы видим, вторая по величине частота равна 16. Она соответствует меховщику Buongiovannino de S.Ambrogio, выступавшему и как свидетель и как сторона договора комменды (трактатор, коммендатор). Следующие по величине частоты (до 9 упоминаний) соответствуют восьми персоналиям, включая упомянутого Ogeriusа – меховщика и одновременно должностного лица консула. В общей сумме они упоминаются 82 раза. Остальные 437 персоналий упоминаются каждый от 8 до 1 раза.

Напомним, что необходимым условием применения предложенного подхода является случайность выборки (это значит, что частота упоминаний, рассматриваемая как случайная величина, имеет равномерное распределение). Простое визуальное наблюдение графика частот на обоих рисунках не позволяет с этим согласиться, что и подтверждается применением критерия χ2 (Пирсона).

Однако, если убрать из рассмотрения первые по частоте 10 персоналий (которые ранее нами были охарактеризованы), то с уровнем значимости 0,1 (то есть достаточно малой вероятностью, при которой событие уже можно считать неслучайным) данное распределение уже будет равномерным. Далее, после удаления указанных 10 элементов объем n выборки сокращается с 866 до 700, а число различных элементов i в ней становится равным 437 (вместо прежних 447). При этом рассчитанное по формуле значение χ2 статистики равно 448,6857, что меньше соответствующего квантиля, равного 475,2005 ^[8]. Все это позволяет перейти к оцениванию объема N генеральной совокупности. Обращаясь к таблице из Приложения 1, получаем: N=678+10=688. Понятно, что это является верхним значением. Так, если мы вернем в рассмотрение исключенные ранее первые 10 элементов и предположим чисто гипотетически, что выборка все же останется случайной, то получающаяся оценка для N становится только меньше (и равной 573).

Все это позволяет сделать вывод, что при заданном уровне значимости 0,1 число потенциальных клиентов генуэзских адвокатов Перы не превосходит величины, равной 688 человек. Довольно неожиданно, что это значение весьма близко результатам А.Л. Пономарева (645-650 купцов), полученным с помощью использования закона Ципфа, а не вероятностного подхода. Необходимо еще раз отметить, что все вышеперечисленные выводы справедливы лишь при условии, что все свои сделки купцы оформляют у нотариев, и выбор того или иного нотария равновероятен.

Приложение 1

Таблица значений функции ]S(i+j,i)[ для определения объема генеральной совокупности (округленные до целых значений функции обозначены квадратными скобками )

Искомый номер N определяется как сумма i и j₀: N=i+j₀, где i – номер строки, а j₀ – номер первого столбца таблицы, при котором значение соответствующего элемента не превосходит n: ]S(N,i) ≤ n (i и n заданы).

Так, при i=437 и n=700 получаем j₀=241 (соответствующий элемент выделен цветом). Отсюда N=678. Аналогично, при i=447 и n=866 получаем N=447+126=573.

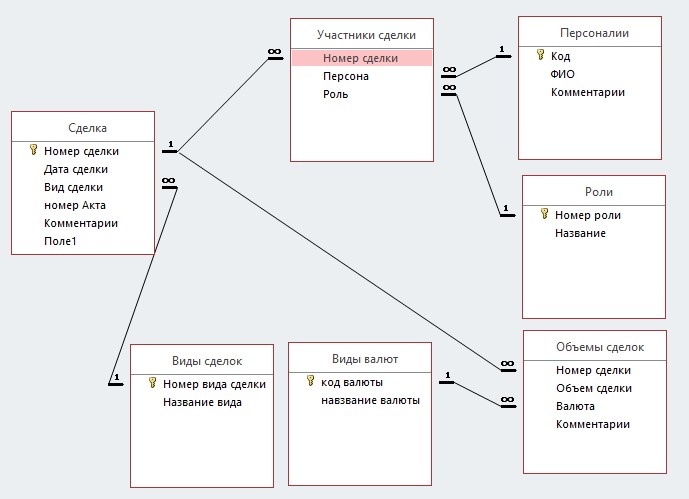
Приложение 2

Схема данных и структура таблиц построенной базы данных по нотариальным актам Предоно 1281 года