Improved CPU load balancing for numerical solution of the tasks of continuous medium mechanics complicated by chemical kinetics

Введение

Существует большое количество задач механики сплошной среды, осложненных необходимостью учета фактора химической кинетики. Назовем задачи моделирования процессов возникновения и распространения пожаров, задачи моделирования процессов образования фотохимического смога на улицах большого города, а также разнообразные технические задачи, связанные с горением. Обычно такие задачи имеют постановку в виде системы дифференциальных уравнений в частных производных, описывающей распространение реагентов, к которой присоединяется система обыкновенных дифференциальных уравнений химической кинетики, описывающая изменение концентраций реагентов в результате химических реакций.

Обычно задачи такого класса решаются итерационно, с применением схем расщепления. При этом на каждой итерации по времени сначала осуществляется шаг численного интегрирования уравнений в частных производных, определяющий изменение концентраций реагентов в ячейках расчетной сетки в результате межъячеечного переноса, а затем выполняется шаг численного интегрирования обыкновенных дифференциальных уравнений химической кинетики. Важной отличительной чертой второго шага является значительное различие скоростей протекания химических реакций в ячейках, если в расчетной области присутствуют существенные тепловые неоднородности. Расчет протекания таких реакций обычно производится жестко устойчивыми методами с контролем шага (например, методом Гира), причем различие скоростей протекания реакций приводит к существенному различию времени интегрирования уравнений химической кинетики в ячейках.

Задачи рассматриваемого класса трудоемки с вычислительной точки зрения и решаются почти исключительно с применением параллельных вычислений, обычно с применением геометрического параллелизма. При этом различие времени, требуемого на интегрирование кинетических уравнений в разных узлах, в условиях тривиального геометрического параллелизма приводит к значительным неоднородностям времени счета областей, относящихся к различным процессорам, что резко снижает эффективность распараллеливания и значительно увеличивает время счета.

Эффективное решение проблемы неоднородности вычислительной загрузки процессоров возможно, если пытаться (на каждой итерации, при осуществлении шага решения уравнений химической кинетики) динамически перераспределять узлы так, чтобы вычислительная неоднородность загрузки процессоров была минимальной.

Такие алгоритмы динамической балансировки загрузки известны ^[1], они обладают различной эффективностью для различных систем. Их можно разделить на следующие группы ^[1]: а) с применением вычисляющей среды ^[2], б) централизованные (см., например, обзор в ^[3]), в) распределенные ^[4], г) диффузные (В.Э.Малышкин, А.П.Карпенко, см. обзор в ^[3], также Cybenko ^[5] и Boillat ^[6]), д) случайные ^[7]. Подробное сравнение алгоритмов проведено в работе ^[1], здесь же отметим следующее:

а) алгоритмы вычисляющей среды могут иметь недостаточно высокую эффективность балансировки, поскольку перераспределение нагрузки между процессорами выполняется фиксированными «слоями» узлов;

б) централизованные алгоритмы имеют сравнительно высокие коммуникационные затраты на взаимодействие центрального процессора с рабочими и, как следствие, недостаточные надежность и эффективность распараллеливания;

в) распределенные алгоритмы часто имеют хорошие показатели по эффективности балансировки и эффективности распараллеливания, и вполне могут быть взяты за основу в настоящей работе;

г) алгоритмы диффузной балансировки осуществляют перераспределение узлов между процессорами, обрабатывающими соседние блоки расчетной области, что также может давать недостаточную эффективность балансировки;

д) алгоритмы случайной балансировки также часто могут давать недостаточную эффективность балансировки, давая средние по качеству балансировки результаты.

В работе ^[1] показано, что для задач с медленным дрейфом «горячих» областей эффективен распределенный алгоритм, при котором распределение нагрузки по процессорам основывается на предполагаемом времени интегрирования, которое считается условно равным времени с предыдущего шага. Недостатком такого подхода к предикции времени является его ограниченная применимость в условиях быстрого дрейфа «горячих» областей. Актуален вопрос об уменьшении данного недостатка.

Целью данной работы является повышение эффективности алгоритма распределенной балансировки загрузки ^[1] и его распространение на случаи с быстрым дрейфом «горячих» областей. Поставим задачи: а) предложить соответствующие модификации алгоритма на базе более совершенных средств предсказания времени интегрирования; б) провести апробацию полученного алгоритма на реальной задаче.

1. Базовый алгоритм

Алгоритм распределенной крупноблочной балансировки ^[1] выполняется на каждом шаге интегрирования системы уравнений химической кинетики. Перед началом шага известна история замеров времени счета для каждого узла-ячейки. Используя эту информацию, каждый процессор определяет предполагаемое время обработки каждого изначально приписанного ему (в соответствии с геометрическим параллелизмом) узла (в базовом варианте считается, что это время равно соответствующему времени с предыдущей итерации, по этой причине базовый вариант успешно применим только в условиях медленного дрейфа «горячих» областей с высоким временем обработки) и делится этой информацией с остальными процессорами. На основании этих данных каждый i-й процессор вычисляет предполагаемую среднюю нагрузку M и определяет, насколько она отличается от его текущей, геометрически распределенной нагрузки R_i. Эта информация используется для априорного перераспределения нагрузки в начале текущего шага.

Процессоры с M < R_i однократно определяют, каким процессорам они будут передавать лишнюю нагрузку, а процессоры с M > R_i однократно определяют, от каких процессоров они примут нагрузку. После этого процессоры приступают к обработке оставшихся «своих» узлов, одновременно с этим выполняются крупноблочные (это позволяет передавать данные более быстро) обмены излишней/недостающей нагрузкой. При завершении обменов процессоры-получатели обрабатывают принятые узлы и алгоритм расчета химической кинетики с балансировкой завершает текущий шаг.

2. Модификация

Предположим, что для предсказания загрузки процессора V_i в каждом i-м узле (i = 1…N, где N – число узлов) можно использовать линейную экстраполяцию, опирающуюся на историю из P предыдущих замеров величины загрузки в i-м узле (это величины H_i,j, j = 1…P). Экстраполяция реализуется линейным соотношением:

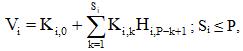
где K_i,k – коэффициенты i-го экстраполятора, S_i – порядок i-го экстраполятора. Такой экстраполятор эквивалентен линейному персептрону из одного нейрона со смещением K_i,0. Персептрон обучается методом наименьших квадратов. В данной работе персептрон программно реализуется авторегрессионным точечным каналом ^[8].

3. Апробация

Рассмотрим нестационарную задачу с относительно быстрым изменением положения «горячих» областей. Пусть это будет двумерное обтекание здания переменным воздушным потоком, причем отмечается тепловая неоднородность: на крыше здания наблюдается процесс горения при высокой температуре.

Проведем несколько численных экспериментов с балансировкой загрузки (на базе линейной экстраполяции) на вычислительной системе с 4-ядерным процессором Intel Atom. Результаты замеров времени решения и расчетов эффективности распараллеливания кинетического блока сведены в таблицу 1. При расчетах использовалась замеренная величина времени решения на одном процессоре T(1) = 299,45 с. Также было замерено и время решения в параллельном варианте (T(N), на N процессорах), но без балансировки – оно составило величину в 195,73 с. Сравнивая эту величину с данными таблицы 1, легко видеть, что балансировка была оправданной.

Таблица 1. Показатели решения с балансировкой (модификация)

Из таблицы 1 очевидно, что расчет по модифицированному алгоритму (S_i = 2) оказался несколько быстрее расчета по базовому алгоритму, соответствующему S_i = 1. Выигрыш составил величину около 2,1% эффективности распараллеливания. В то же время вариант с S_i = 3 не только не дал прироста производительности, но и снизил ее. Это может объясняться двумя причинами: а) ростом затрат на собственно предикцию, которые превысили эффект выравнивания загрузки, б) некорректностью предикции (предиктор реализует фиктивные или частные зависимости, использующие чрезмерно большое количество предыдущих точек). Тем не менее, можно предположить, что модификации алгоритма при S_i > 2 могут найти применение в каких-либо еще более сложных случаях.

Заключение

В данной работе предложена модификация алгоритма крупноблочной распределенной балансировки, основанная на применении линейного персептрона для предсказания времени интегрирования в узлах, пригодна для случаев как с медленным, так и с относительно быстрым дрейфом "горячих" областей. Модификация апробирована в задаче о моделировании обтекания одиночного здания с горением на крыше (случай быстрого дрейфа "горячих" областей). Показано, что применение модифицированного алгоритма повышает эффективность распараллеливания на 2,1% по сравнению с исходным алгоритмом.