|
DOI: 10.25136/2644-5522.2020.1.33213
Received:
14-06-2020
Published:
03-07-2020
Abstract:
The article presents a dynamic socio-ecological-economic model of the synergetic development of individual economic entities, which makes it possible to reconcile their general and private interests. Maximization of specific consumption is proposed as a target parameter. Accordingly, in relation to private interests - the subject, in relation to general interests - the governing center. The model provides for the possibility of using the available resources by each entity both in the tasks of their own development and in the general development goals of other entities. The presented model can be used to form an economic development program for a separate territory, a separate industrial cluster, a municipality, a region and a macro-region. As a result of modeling, control parameters are formed for developing a strategy for economic development. A model of territorial development based on two models is presented: a dynamic model of the combination of general and private interests and a neoclassical Solow model. It is proposed to use a model for regional systems, where the elements of the system are regions within one macro-region. The parameters of the model used for the macroregion are described in terms of identification. The modification of the Solow model takes into account a) threshold limits on the volume of production in the region, emissions and discharges of pollutants from the regions; b) interaction of subjects in solving joint development problems through cross-investment for a synergistic effect; c) taking into account the influence of technical progress both on the volume of the quantity of products produced and on labor productivity. As for the use of the model of the combination of general and private interests, the sum of two terms was taken as the target function of agents (regions): the maximization of specific consumption is taken as the private interests of the region, and the specific consumption of the entire macroregion is taken as the general interest.
Keywords:
modeling, combining, social interests, private interests, combining development, development control, dynamic model, specific consumption, economical subjects, control center
Методика моделирования социо-эколого-экономического развития субъектов на базе теории оптимального управления предложена в работах В.И. Гурмана с соавторами [11]. В задачах исследования согласованного развития использовались аналитические методы наряду с имитационным моделированием.
В монографии Дружинина и Угольницкого [9] хорошо известная макроэкономическая модель Солоу [10] модифицирована с учетом пространственного аспекта и загрязнения окружающей среды. Детальный обзор моделей и систем поддержки решений в области управления устойчивым развитием представлен в работах Угольницкого [3] и моделей экономического роста [1].
Важный класс динамических моделей экономического развития территорий образуют Computable General Equilibrium (CGE) models [2, 3]. Эти модели имеют прочное микроэкономическое обоснование и обеспечивают полноту учета отраслевой структуры хозяйства, а также воздействия изменений в одних экономических секторах на другие. Основной недостаток CGE-моделей состоит в том, что они по сути экономико-математические и недостаточно хорошо описывают экологические и социальные аспекты, а также эффекты, связанные с динамикой и неопределенностью; их идентификация также затруднена.
В работах О.И. Горбаневой и Г.А. Угольницкого предложен оригинальный комплексный подход к моделированию согласования частных и общественных интересов при распределении ресурсов в иерархических системах управления [2, 8]. При реализации указанного подхода: получены условия системной согласованности для различных постановок задач управления; предложены механизмы системного согласования и изучены их свойства; начата работа по приложению моделей согласования общественных и частных интересов к управлению развитием территорий, а именно построению административных и экономических механизмов согласования интересов территориальных субъектов [2, 5-8].
В данной статье изложены результаты исследований по развитию моделей согласования общественных и частных интересов к управлению обособленными экономическим субъектами, в качестве которых могут выступать агенты обособленного промышленного кластера, предприятия муниципального образования, системы региона и макрорегиона.
В ходе исследования рассматривается оптимальное поведение агентов с целью повышения как собственного удельного потребления, так и повышение удельного потребления системы. Для достижения этой цели субъекты могут тратить имеющиеся у них средства как на свое развитие, так и развитие соседних субъектов.
Далее рассмотрим модель взаимодействия обособленных экономических субъектов социо-эколого-экономической системы:
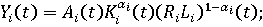 (1) (1)
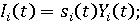 (2) (2)
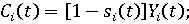 (3) (3)
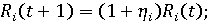 (4) (4)
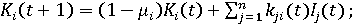 (5) (5)
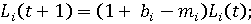 (6) (6)
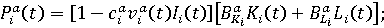 (7) (7)
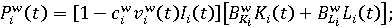 (8) (8)
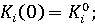 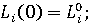 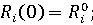 (9) (9)
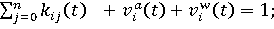 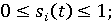 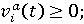 (10) (10)
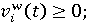 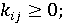 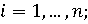 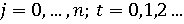 (11) (11)
Индекс 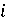 обозначает номер экономического субъекта в системе. обозначает номер экономического субъекта в системе.
Время 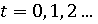 в модели дискретно и изменяется с шагом в один год. в модели дискретно и изменяется с шагом в один год.
Обозначения переменных и параметров модели:
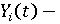 конечный продукт субъекта в финансовом выражении в году t; конечный продукт субъекта в финансовом выражении в году t;
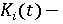 основные производственные фонды субъекта в финансовом выражении (капитал) агента в году t; основные производственные фонды субъекта в финансовом выражении (капитал) агента в году t;
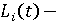 трудовые ресурсы субъекта в году t; трудовые ресурсы субъекта в году t;
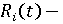 эффективность трудовых ресурсов субъекта в году t; эффективность трудовых ресурсов субъекта в году t;
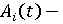 функция влияния инновационной активности субъекта на производство конечного продукта в году t; функция влияния инновационной активности субъекта на производство конечного продукта в году t;
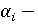 параметр производственной функции Кобба-Дугласа для субъекта; параметр производственной функции Кобба-Дугласа для субъекта;
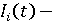 величина производственных инвестиций субъекта в году t; величина производственных инвестиций субъекта в году t;
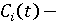 объем непроизводственного потребления субъекта в году t; объем непроизводственного потребления субъекта в году t;
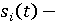 доля производственных инвестиций субъекта в его конечном продукте в году t; доля производственных инвестиций субъекта в его конечном продукте в году t;
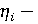 параметр роста эффективности трудовых ресурсов субъекта; параметр роста эффективности трудовых ресурсов субъекта;
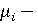 коэффициент амортизации основных фондов субъекта; коэффициент амортизации основных фондов субъекта;
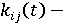 доля инвестиций i-го субъекта в деятельность j-го субъекта (коэффициент взаимодействия между субъектами); здесь индекс j=0 означает внешнего по отношению к системе субъекта; доля инвестиций i-го субъекта в деятельность j-го субъекта (коэффициент взаимодействия между субъектами); здесь индекс j=0 означает внешнего по отношению к системе субъекта;
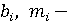 коэффициенты воспроизводства и выбытия трудовых ресурсов для субъекта; коэффициенты воспроизводства и выбытия трудовых ресурсов для субъекта;
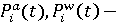 выбросы субъекта загрязняющих веществ в атмосферу и воду соответственно в году t; выбросы субъекта загрязняющих веществ в атмосферу и воду соответственно в году t;
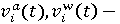 ассигнования субъекта на борьбу с загрязнением атмосферы и воды соответственно в году t; ассигнования субъекта на борьбу с загрязнением атмосферы и воды соответственно в году t;
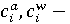 коэффициенты эффективности природоохранных ассигнований; коэффициенты эффективности природоохранных ассигнований;
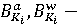 удельные выбросы загрязняющих веществ при производственной деятельности в атмосферу и воду соответственно; удельные выбросы загрязняющих веществ при производственной деятельности в атмосферу и воду соответственно;
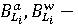 удельные выбросы загрязняющих веществ при жизнедеятельности трудовых ресурсов в атмосферу и воду соответственно; удельные выбросы загрязняющих веществ при жизнедеятельности трудовых ресурсов в атмосферу и воду соответственно;
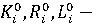 заданные начальные значения соответствующих переменных модели. заданные начальные значения соответствующих переменных модели.
Таким образом, вектор состояния субъекта есть:
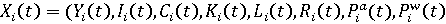 ), (12) ), (12)
вектор управляющих воздействий:
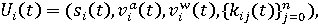 (13) (13)
вектор параметров
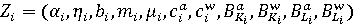 . (14) . (14)
В качестве исходных параметров модели предлагается использовать следующие значения статистических данных:
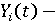 валовый объем производства (В); валовый объем производства (В);
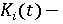 объем основных производственных фондов (ОПФ); объем основных производственных фондов (ОПФ);
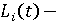 численность трудовых ресурсов; численность трудовых ресурсов;
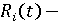 валовая выработка, отношение произведенной продукции к затратам труда; валовая выработка, отношение произведенной продукции к затратам труда;
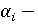 эластичность производства по основным фонда; эластичность производства по основным фонда;
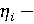 прирост (динамика) выработки; прирост (динамика) выработки;
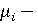 износ ОПФ, доля стоимости, перенесенная на произведенный продукт (В); износ ОПФ, доля стоимости, перенесенная на произведенный продукт (В);
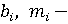 соответственно прирост и убыль трудовых ресурсов; соответственно прирост и убыль трудовых ресурсов;
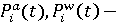 выбросы субъектом загрязняющих веществ в атмосферу и воду соответственно в году t. выбросы субъектом загрязняющих веществ в атмосферу и воду соответственно в году t.
Взаимодействие субъектов предлагается описывать с помощью управляющих переменных 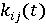 . Параметр . Параметр 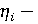 характеризует уровень производительности труда; параметр характеризует уровень производительности труда; параметр 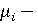 позволяет определить применение ресурсосберегающих технологий; группа параметров позволяет определить применение ресурсосберегающих технологий; группа параметров 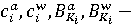 описывает применение природоохранных технологий; параметр описывает применение природоохранных технологий; параметр 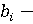 позволяет учесть демографическую динамику; параметр позволяет учесть демографическую динамику; параметр 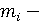 отражает уровень безопасности трудовых ресурсов на производстве; параметры отражает уровень безопасности трудовых ресурсов на производстве; параметры 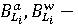 характеризуют экологическую ответственность субъектов. характеризуют экологическую ответственность субъектов.
Критерий оптимальности субъекта в модели (1)-(11) естественно определить, как функцию сочетания общих и частных интересов:
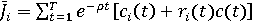 . (15) . (15)
где 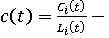 текущее удельное потребление субъекта, выступающее частным интересом; текущее удельное потребление субъекта, выступающее частным интересом;
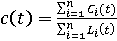 – удельное потребление системы субъектов, которое выступает общим интересом, – удельное потребление системы субъектов, которое выступает общим интересом,
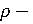 коэффициент дисконтирования, коэффициент дисконтирования,
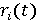 – отражает заинтересованность субъекта в повышении удельного потребления системы. – отражает заинтересованность субъекта в повышении удельного потребления системы.
Заинтересованность субъекта в максимизации не только внутреннего удельного потребления, но и всех соседних субъектов, а, следовательно, и всей системы означает стремление повысить общую экономическую эффективность сотрудничества. Соответственно, чем меньше разница в параметрах потребления субъектов, тем лучше инвестиционная привлекательность субъектов, ниже уровень социальной напряженности системы, благоприятнее общая экономическая динамика, которая определяет затраты на реализацию совместных проектов и программ развития.
Сценарии имитации в модели (1)-(11) включают задание траекторий управляющих переменных из вектора (15).
Для исследования взаимодействий субъектов в составе системы нужно произвести идентификацию параметров векторов Zi для каждого субъекта, а также произвести расчеты главных показателей на конкретных данных, конкретно 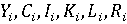 на выбранном временном промежутке. на выбранном временном промежутке.
Параметры модели 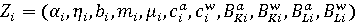 и коэффициент Ai(t) могут быть идентифицированы по фактическим данным. и коэффициент Ai(t) могут быть идентифицированы по фактическим данным.
Прочие параметры должны быть идентифицированы в зависимости от масштабов рассматриваемой системы субъектов экономических отношений.
Таким образом, в работе представлена динамическая модель сочетания общих и частных интересов (СОЧИ-модель) на основе неоклассической модели СОЛОУ с учетом пороговых ограничений на объем производства, выбросы и сбросы загрязняющих веществ. Данная модель предполагает взаимодействие субъектов в решение совместных задач развития за счет перекрестных инвестиций в целях синергетического эффекта.
Дальнейшее развитие проблематики предполагает исследование разработанной модели на фактических данных с формированием практических рекомендаций в части разработки экономических стратегий поведения субъектов системы с учетом управляющих параметров.
References
1. Barro, R. J., & Sala-i-Martin, X. Economic growth 2e. Cambridge, MA: The MIT Press, 2004. S.160
2. Gorbaneva, O. I., Ougolnitsky, G. A. System Compatibility: Price of Anarchy and Control Mechanisms in the Models of Concordance of Private and Public Interests // Advances in Systems Science and Applications, 15(1), 2015. S. 45-59.
3. Ougolnitsky, G. A., Usov, A. B. Computer Simulations as a Solution Method for Differential Games // Computer Simulations: Advances in Research and Applications. Eds. MD Pfeffer and E. Bachmaier. NY: Nova Science Publishers, 2018. S. 63-106.
4. Partridge, M. D., Rickman, D. S. Computable general equilibrium (CGE) modelling for regional economic development analysis. Regional studies, 44(10), 2010. S. 1311-1328.
5. Anopchenko, T. Yu., Murzin, A. D., Ugol'nitskii, G. A. Modelirovanie soglasovaniya interesov v zadachakh upravleniya ustoichivym razvitiem territorii. Ekonomika prirodopol'zovaniya, (6), 2017. S. 35-47.
6. Ougolnitsky, G., Anopchenko, T., Gorbaneva, O., Lazareva, E., Murzin, A. Systems Methodology and Model Tools for Territorial Sustainable Management. Advances in Systems Science and Applications, 18(4), 2018. S. 136-150. https://doi.org/10.25728/assa.2018.18.4.584
7. Anopchenko, T. Yu., Murzin, A. D. Upravleniya riskami investitsionno-stroitel'nykh proektov razvitiya urbanizirovannykh territorii: monografiya. Rostov n/D: Rost. gos. stroit. un-t. 2012. S. 124.
8. Gorbaneva, O. I., Murzin, A. D., Ugol'nitskii, G. A. Mekhanizmy soglasovaniya interesov pri upravlenii proektami razvitiya territorii. // Upravlenie bol'shimi sistemami: sbornik trudov, (71), 2018. S. 61-97.
9. Druzhinin, A. G., Ugol'nitskii, G. A.. Ustoichivoe razvitie territorial'nykh sotsial'no-ekonomicheskikh sistem: teoriya i praktika modelirovaniya. M.: Vuzovskaya kniga, 2013. S. 224.
10. Lotov, A. V. Vvedenie v ekonomiko-matematicheskoe modelirovanie (Vol. 350). M.: Nauka. 1984. S. 392.
11. Modelirovanie sotsio-ekologo-ekonomicheskoi sistemy regiona. Pod red. V.I. Gurmana, E.V. Ryuminoi. M.: Nauka, 2001. S. 172.
|
















 This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

