|
DOI: 10.7256/2585-7797.2020.1.32205
Received:
17-02-2020
Published:
11-04-2020
Abstract:
The article sets a problem focusing on how to optimize the order of 3D user interface for virtual reconstruction of Moscow historical center landscape in the 16th-18th centuries. To work with the interface a virtual reality headset, a motion tracking system and an eye-tracker were integrated. Spatial representation of the historical reconstruction is accompanied by a specialized interface that allows one to access the source database. The authors introduce a criterion that provides for estimating the optimum order of interface elements in the virtual space. The problem is handled in case there are unknown factors such as the size of user's hands, deviations in the position of an interactive object and restrictions related to the disposition of interface elements. The article sets the general problem and solves some internal problems related to the construction of acceptable multiple dispositions of interface elements and the modeling of eyesight movement from one interface element to another. The article is the first to suggest an algorithm to numerically optimize the interface in 3D virtual space modeling the relief and historical buildings in the center of Moscow. It provides for user’s movement and gives access to historical sources which are the basis for virtual reconstruction of the heritage understudy.
Keywords:
Virtual reality, Mixed reality, Historical virtual reconstruction, Historical city landscape, Belyi Gorod, Motion tracking, Virtual interface, Reachability set, Game theory, Oculography
Виртуальная реконструкция объектов историко-культурного наследия, основанная на технологиях 3D моделирования, активно развивается в течение последнего десятилетия. В центре внимания создателей научных виртуальных реконструкций объектов, утраченных полностью или частично, находятся источниковедческие вопросы, решение которых должно обеспечить достаточную степень достоверности создаваемых 3D моделей [1]. В связи со стремительным развитием технологий виртуальной и дополненной реальности (VR/AR) такие разработки могут теперь включать новую компоненту, целью которой является, с одной стороны, расширение познавательных возможностей пользователя виртуальной реконструкции за счет иммерсионных эффектов VR; с другой стороны, использование VR/AR технологий повышает мотивацию при изучении истории культуры и смежных дисциплин. Эти технологии позволяют «погрузить» обучаемого в виртуальную среду, которая воспринимается им через органы чувств. Одна из первых разработок такого рода была осуществлена в рамках исследовательского проекта по виртуальной реконструкции Страстного монастыря [2].
Реализация технологии виртуальной реальности включает следующие основные шаги [3, с.89]: компьютер создает образ (трехмерное изображение объектов в виртуальной среде); программная система отображения транслирует его на органы чувств пользователя; установленные на теле пользователя датчики передают компьютеру информацию о действиях/движениях пользователя (например, о повороте головы, движениях рук или изменении его положения в пространстве); компьютер использует эту информацию для изменения генерируемой им виртуальной реальности и ее образа, который передается на органы чувств пользователя. Используемое VR-оборудование (гарнитуры) позволяет пользователю взаимодействовать с виртуальной реальностью, погружаться в нее, совершать передвижения, видеть и слышать виртуальный мир [3, с.90].
* * *
В лаборатории математического обеспечения имитационных динамических систем (МОИДС) Московского государственный университета им. М.В. Ломоносова создано аппаратное и программное обеспечение для применения технологии виртуальной реальности при тестировании и моделировании интерактивных виртуальных исторических реконструкций. Реалистичный пользовательский опыт был достигнут с использованием глубокой обратной связи, которая активирует большое количество биологических сенсоров человека, включая зрение.
Для достижения реалистичной визуализации в лаборатории был разработан комплекс на основе шлема виртуальной реальности высокого разрешения (HMD).
Вход системы визуализации дает информацию о состоянии математической модели пользователя и окружающих его объектов виртуального мира, что позволяет моделировать взаимодействие в режиме реального времени. Одной из характеристик HMD является полное покрытие поля зрения пользователя и замена реальной среды виртуальной моделью. Применяется система отслеживания движения для передачи движения реального человека в виртуальное пространство [4]. Подобный подход был назван «смешанной реальностью».
Система смешанной реальности представляет собой программно-аппаратный комплекс, выполняющий функцию визуализации ближайшего окружения для пользователя с возможностью отслеживания движений человека и передачи этих движений в виртуальное пространство. Технология создает иллюзию абсолютного физического присутствия человека в виртуальном пространстве.
Задача, которая рассматривается в данной статье, была поставлена в ходе исследований по созданию виртуальных реконструкций, проводимых сотрудниками кафедры исторической информатики исторического факультета МГУ. В рамках совместного проекта кафедры и лаборатории МОИДС создается виртуальная реконструкция исторического ландшафта и ряда доминантных объектов исторической застройки Белого города (территории в центре Москвы) XVI-XVIII веков [5]. Реконструкция будет представлена в формате виртуальной реальности. Одна из основных задач – в ходе перемещений пользователя в виртуальной среде обеспечить ему доступ не только к самой реконструкции, но и к источниковой базе, на основе которой создается эта реконструкция. Для ее верификации используется виртуальный пространственный интерфейс.
Размер, детализация и масштаб являются основными опциями для правильного иммерсионного представления данных в среде виртуальной реальности. При использовании комплекса смешанной реальности для верификации виртуальной реконструкции, важным аспектом становится взаимодействие с элементами виртуального интерфейса, что потребовало разработки новых методов и адаптации алгоритмов отслеживания и визуализации движений человека.
Отслеживание движения человека должно выполняться с частотой не менее 60 Гц. Ультразвуковые и радиосистемы отслеживания движения не могут обеспечить необходимую частоту для более чем одного датчика, а магнитные работают некорректно при наличии стороннего оборудования. В рамках нашего проекта используется комбинация оптических и инерциальных датчиков. Существующие оптические системы отслеживания движения имеют требуемую частоту, но они чувствительны к перекрытию оптических маркеров - в эти моменты данные от оптических систем отсутствуют или неверны. Инерциальные системы не подвержены перекрытию, однако имеют низкую точность при отслеживании линейного перемещения с ошибками, накопленными с течением времени. Разработка гибридной системы слежения как комбинации оптических и инерциальных данных дала возможность получить решение без указанных проблем [6].
Постановка задачи численной оптимизации интерфейса
Точное отслеживание движений дает возможность пользователю свободно взаимодействовать с виртуальным интерфейсом. Каждый объект виртуальной реконструкции снабжен исторической справкой и интерактивными элементами, позволяющими открыть меню, изменить состояние объекта или получить доступ к соответствующему историческому источнику, используемому для верификации. Задача может быть условно разделена на две задачи: расположение элементов информационного интерфейса и расположение интерактивных элементов.
Несмотря на некоторое различие между информацией и интерактивными элементами, данная статья предлагает общий подход к поиску эффективной позиции для них обоих.
Расположение элементов интерфейса в трехмерном пространстве не предполагает эмпирического подхода к задаче, в отличие от двумерного интерфейса на экране компьютера, где может применяться закон Фиттса [7]. Это вызвано новыми возможностями виртуальной реальности для размещения элементов в пространстве без какой-либо привязки к физическим объектам.
Например, если мы рассмотрим куб размером 0,5 метра в качестве допустимого пространства для размещения интерактивных элементов, точность позиционирования в виртуальной реальности составляет 1 см, мы получим около 1010 экспериментов для двух элементов интерфейса без учета возможных различий в параметрах человека. В то же время высота и длина руки пользователя больше всего влияют на удобство использования виртуального интерфейса. Точно так же различные трехмерные модели в сцене, которые могут перегородить обзор, усложняют задачу визуального отслеживания.
При работе с малым количеством элементов интерфейса бывает достаточно использовать интерфейсную плоскость. Такой подход был применен в интерфейсе реконструкции Страстного монастыря (рис. 1).
 Рис. 1. Виртуальный интерфейс Рис. 1. Виртуальный интерфейс
Увеличение количества объектов, отображаемых одновременно, показало недостатки этого метода: интерфейс либо оказывался не привязанным к соответствующим объектам, либо перекрывал обзор.
В данной работе представлен новый подход, который учитывает все мешающие факторы и позволит генерировать зону приоритетного расположения элементов интерфейса в трехмерном пространстве.
Для простоты элемент интерфейса будет рассматриваться как точка (множество допустимых положений элементов интерфейса считаем замкнутым).
Предположим, что существует динамическая система, которая описывает движение глаза или руки (примеры системы будут приведены далее):
|
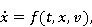
|
(1)
|
где 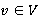 — вектор возмущенных параметров системы. — вектор возмущенных параметров системы.
В паре элементов интерфейса первый элемент будет начальными условиями, а второй - конечными условиями. Время целенаправленного движения от первого элемента ко второму мы будем рассматривать как функционал качества:
|
|
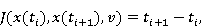
|
(2)
|
где 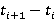 — время движения, определенное экспериментом или оптимальным по времени решением задачи. — время движения, определенное экспериментом или оптимальным по времени решением задачи.
Зададим задачу оптимизации позиций элементов интерфейса (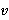 предопределено): предопределено):
|
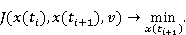
|
(3)
|
Очевидно, что тривиальное минимальное решение задачи заключается в расположении элементов интерфейса в одной точке. Однако в приложениях необходимо поддерживать некоторое расстояние между элементами интерфейса, чтобы дать возможность пользователю сознательно выбирать между ними. Кроме того, виртуальная среда накладывает некоторые ограничения, поскольку элементы интерфейса должны быть расположены вне трехмерных объектов.
Опишем наложенные ограничения следующим образом:
|
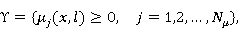
|
(4)
|
где 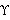 - множество ограничений на позиции элементов интерфейса. - множество ограничений на позиции элементов интерфейса.
В реальной задаче может быть более двух элементов интерфейса, и вероятности перехода могут отличаться попарно. Определим эти вероятности как коэффициенты 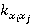 веса каждого перехода (от веса каждого перехода (от 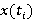 до до 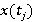 ) за все время работы. ) за все время работы.
Для виртуальных интерфейсов можно искать оптимальное время перехода для каждой пары независимо от других переходов и ограничений, накладываемых на расположение других элементов.
В результате, если 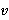 предопределено, для предопределено, для 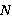 элементов интерфейса мы получаем задачу минимизации взвешенной суммы. Стоит отметить, что последовательность перехода не является фиксированной. элементов интерфейса мы получаем задачу минимизации взвешенной суммы. Стоит отметить, что последовательность перехода не является фиксированной.
|
|
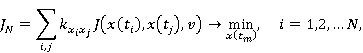
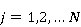
|
(5)
|
Здесь 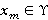 — все возможные местоположения элементов интерфейса, между которыми происходит переход. — все возможные местоположения элементов интерфейса, между которыми происходит переход.
Как указано выше, задача будет решена для информационных и интерактивных интерфейсов. Тем не менее, интерактивные элементы могут функционировать как информационные, но это выходит за рамки нашей работы, содержащей основные результаты, которые станут основой для решения всей задачи. Для информационных элементов мы рассмотрели бинокулярную модель движения глаз, и задача оптимального перехода была решена и подтверждена экспериментально. Для интерактивных элементов мы создали набор достижимости рук человека и провели серию экспериментов, которые необходимы для определения параметров модели руки.
Предложенные алгоритмы и соответствующий математический аппарат даются в Приложении.
* * *
В заключение отметим, что предложенный в данной работе алгоритм оптимизации пространственного интерфейса виртуальной реальности предназначен для организации передвижений пользователя в виртуальной среде, обеспечения интерактивного взаимодействия с элементами воссозданной исторической виртуальной реконструкции.
Применение предложенного подхода в исследовании эволюции ландшафта Белого города XVI — XVIII вв. позволяет существенно упростить задачи расположения элементов интерфейса в пространстве исторической виртуальной реконструкции рассматриваемой территории центра Москвы. Тем самым достигается расширение познавательных возможностей пользователя виртуальной реконструкции за счет иммерсионных эффектов, которые создают новейшие технологии VR.
ПРИЛОЖЕНИЕ
Анализ движения глаз человека
Стерео контент, воспроизводимый в системе виртуальной реальности, отличается тем, что рабочая область не ограничена плоскостью изображения и экраном. Когда появляется пространственная задача, необходимо учитывать бинокулярное зрение.
Когда мы смотрим на элемент данных интерфейса, наши глаза делают сходящиеся (конвергентные) движения, чтобы сфокусироваться на объекте. Отдельно стоит отметить работу со сложными сценами, такими как исторический ландшафт с набором зданий и элементов интерфейса. Возможная «перегруженность» виртуальной сцены приведет к длительному решению пользователем задачи поиска нужного элемента. По этой причине исследование движений глаз представляет интерес и для оптимизации интерфейса, и для оценки полученного результата.
Математическая модель движения глаз обычно учитывает только один глаз. Применение этой модели для скоординированных движений обоих глаз увеличивает порядок задач.
Перенос взгляда с одного элемента интерфейса на другой всегда осуществляется саккадой - быстрым скоординированным движением глаз. Здесь мы рассматриваем целенаправленное движение пары глаз как оптимальное по времени решение задачи.
Возьмем динамическую модель, основанную на мышечной модели Фельдмана [8], чтобы моделировать каждый глаз пары:
|
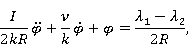
|
(6)
|
где 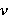 — коэффициент вязкости глаза по среде, — коэффициент вязкости глаза по среде, 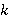 — коэффициент эластичности мышц, — коэффициент эластичности мышц, 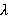 — длина мышцы, — длина мышцы, 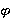 — угол поворота глаза, — угол поворота глаза,  — радиус глаза. В рамках модели принято, что только одна пара глазодвигательных мышц (ГДМ) действует на вращение глаза в горизонтальной, фронтальной и сагиттальной плоскостях. Обе мышцы имеют одинаковые пружинные и вязкие коэффициенты и различную свободную длину λ. Для простоты рассмотрим движение глаза в горизонтальной плоскости. Предположим, что каждый глаз совершает только вращательное движение вокруг своего геометрического центра. — радиус глаза. В рамках модели принято, что только одна пара глазодвигательных мышц (ГДМ) действует на вращение глаза в горизонтальной, фронтальной и сагиттальной плоскостях. Обе мышцы имеют одинаковые пружинные и вязкие коэффициенты и различную свободную длину λ. Для простоты рассмотрим движение глаза в горизонтальной плоскости. Предположим, что каждый глаз совершает только вращательное движение вокруг своего геометрического центра.
Крутящий момент глазных мышц не может измениться мгновенно. Мы можем формализовать этот факт с помощью следующего уравнения:
|
|
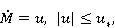
|
(7)
|
где 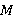 — крутящий момент, создаваемый парой ГДМ, управление — крутящий момент, создаваемый парой ГДМ, управление 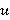 — скорость изменения крутящего момента ГДМ. Начальные и конечные условия крутящего момента ГДМ рассчитываются для каждой начальной и конечной позиции глаза. Очевидно, что систему (6) и (7) можно представить в виде (1). — скорость изменения крутящего момента ГДМ. Начальные и конечные условия крутящего момента ГДМ рассчитываются для каждой начальной и конечной позиции глаза. Очевидно, что систему (6) и (7) можно представить в виде (1).
Движение глаз моделируется путем решения оптимальной по времени задачи при переходе от начальных условий к некоторым конечным. Для решения задачи переноса взгляда двух глаз с цели на цель было использовано решение из [9].
Результаты математического моделирования были сопоставлены с экспериментальными данными. Было проанализировано движение глаз, записанное с помощью высокоскоростной окулографической системы SMI Hi-Speed 1250 с частотой 500 Гц, регистрирующей движение двух глаз. Система представляет собой рамку с лбом и держателем для подбородка, на которой закреплена высокоскоростная камера и отражающее стекло, ЖК-экран для создания визуального стимула и персональный компьютер с установленным на нем программным обеспечением для проведения экспериментов и обработки записей.
Данные представлены в исследовании [10]. В эксперименте приняли участие 9 человек в возрасте от 18 до 22 лет с нормальной остротой зрения, без очков или линз; не выявлены заболевания нервной системы и расстройства органов внутреннего уха. Участники исследования сидели неподвижно и наблюдали за движением цели по экрану (стимулы). Серия для одного человека состояла из 84 стимулов. Цель двигалась из точки в точку на сетке размером 7 x 9.
Стимулы были представлены один за другим. Цель выглядела как белый круг на черном фоне. В центре белого круга в части раздражителей отображалась точка в 1 пиксель красного, синего или зеленого цветов. Человека попросили подсчитать количество точек определенного цвета. Было необходимо не только увидеть появившуюся цель, но и точно посмотреть на нее.
Полученные результаты сравнения модельных данных с реальными показали возможность применения описанной модели для исходной задачи работы с интерфейсом. Возмущения начальных условий, предложенные в [10], могут рассматриваться как тестирующие.
Множество ограничений на расположение интерактивных элементов интерфейса
Для описания целенаправленных движений глаз и рук обычно решаются оптимальные по времени задачи. Обе задачи довольно близки, но ограничения для интерактивных элементов более сложны. Было построено много возможных позиций рук, описывающих набор ограничений (4) для элементов интерактивного интерфейса.
Параметры кисти и модель движения руки записываются в предположении, что плечо зафиксировано. Фиксированная система координат вводится с началом в центре вращения в плечевом суставе, ось  направлена вперед от человека, ось направлена вперед от человека, ось  направлена влево, ось направлена влево, ось  направлена вертикально вверх. направлена вертикально вверх.
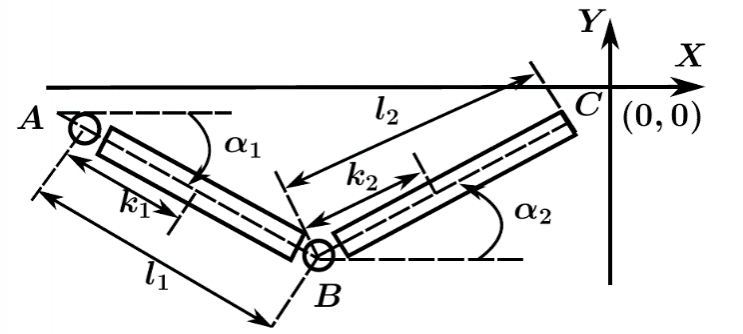 Рис. 2. Модель руки Рис. 2. Модель руки
Рука моделируется трехзвенным механизмом (рис. 2). Звенья связаны цилиндрическими соединениями. Ось плечевого сустава фиксирована. В качестве обобщенных координат принимаются следующие: угол между прямым направлением и звеном 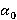 , углы между звеньями и горизонталью соответственно , углы между звеньями и горизонталью соответственно 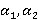 . Также используются следующие обозначения: длина ссылок . Также используются следующие обозначения: длина ссылок 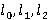 , массы , массы 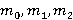 , центральные моменты инерции , центральные моменты инерции 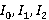 . Введем коэффициенты, которые определяют относительное положение центра масс звена на его продольной оси, . Введем коэффициенты, которые определяют относительное положение центра масс звена на его продольной оси, 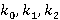 , определяемое из равенств: , определяемое из равенств:
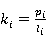 , ,
где 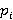 — расстояние от — расстояние от 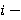 го сустава до центра масс. го сустава до центра масс.
Были использованы данные из работы [11] для построения набора достижимости для ручных ссылок. В таблице ниже перечислены ограничения для допустимых углов при вращении вокруг разных осей для большинства людей.
На рис. 3 показаны измеренные углы и их центральные точки. Следует отметить, что на каждой фигуре есть позиции А и В. В таблице показаны не все эти позиции, например, угол B указан для горизонтального похищения, поскольку сумма углов A и B равна 180 °. Также сумма углов сгибания / разгибания предплечья составляет 180 °.
Введем угол 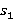 как угол вертикального сгибания плеча, как угол вертикального сгибания плеча, 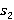 как угол горизонтального сгибания / разгибания, длина плеча — как угол горизонтального сгибания / разгибания, длина плеча — 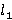 . Угол . Угол 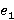 соответствует вертикальному углу сгибания предплечья, соответствует вертикальному углу сгибания предплечья, 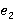 — латерально-медиальному углу сгибания, длина предплечья — — латерально-медиальному углу сгибания, длина предплечья — 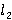 . .
Тогда координаты кисти руки 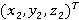 будут выражаться следующим образом: будут выражаться следующим образом:
|

|
(8)
|
На рис. 3 показан пример формы множества достижимости для руки (предплечье движется, плечо фиксировано).
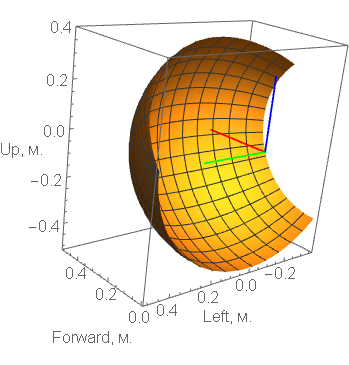
Рис. 3. Множество достижимости для руки (предплечье движется, плечо фиксировано)
Система (8) показывает, как мы можем вычислить множество допустимых положений объекта интерфейса (4), когда определены параметры руки (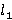 , , 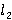 ). Мы должны пересчитать его для каждого ). Мы должны пересчитать его для каждого 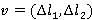 . .
Задача оптимизации интерфейса при наличии возмущений
В первой части этой статьи была поставлена задача оптимизации расположения элементов интерфейса с определенными параметрами системы (1).
Для каждого объекта в виртуальной сцене сам объект является статическим, но параметры человека (пользователя) могут значительно отличаться от первоначально выбранных.
Можно использовать алгоритм идентификации параметров в режиме реального времени и решить задачу оптимизации интерфейса для каждого пользователя, рассмотренного в первой части статьи. Однако это можно сделать только для небольшого числа элементов интерфейса и со значительными ограничениями их взаимного расположения.
Задача оптимального размещения элементов интерфейса усложняется, если невозможно провести идентификацию, поскольку необходимо учитывать наихудшие возможные параметры.
Альтернативный подход – использовать теорию игр [12]. Действительно, пусть длины звеньев, массы и т. д. будут возмущениями. Мы будем рассматривать относительное положение элементов интерфейса в качестве управления. Как и ранее, функционал 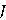 - взвешенная сумма времен перехода между элементами интерфейса. - взвешенная сумма времен перехода между элементами интерфейса.
Если игрок, ответственный за возмущения, пытается максимизировать функционал, а игрок, ответственный за управление, минимизирует, то мы получаем антагонистическую игру Γ.
Мы будем рассматривать минимум управлений от максимума возмущений от 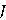 как оценку качества интерфейса: как оценку качества интерфейса:
|
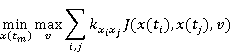
|
(9)
|
Чтобы найти оптимальное решение, можно использовать методы динамического программирования [13]. Из-за большого количества переменных проблема является масштабной и требует большого объема вычислений и ресурсов памяти.
References
1. Borodkin L. I. Strastnoi monastyr' v XVII-XX vv.: prostranstvennaya evolyutsiya i virtual'naya rekonstruktsiya // Rossiiskaya istoriya — 2016. — № 5. — S. 149–160
2. Borodkin L.I., Mironenko M.S., Chertopolokhov V.A., Belousova M.D., Khlopikov V.V. — Tekhnologii virtual'noi i dopolnennoi real'nosti (VR/AR) v zadachakh rekonstruktsii istoricheskoi gorodskoi zastroiki (na primere moskovskogo Strastnogo monastyrya) // Istoricheskaya informatika. – 2018. – № 3. – S. 76 - 88. DOI: 10.7256/2585-7797.2018.3.27549 URL: https://nbpublish.com/library_read_article.php?id=27549
3. Uvarov A.Yu. Obrazovanie v mire tsifrovykh tekhnologii: na puti k tsifrovoi transformatsii Izd. dom GU-VShE, M.: 2018. — 168 s.
4. Bugrov D. I., Lebedev A. V., Chertopolokhov V. A. Otsenka uglovoi skorosti vrashcheniya tela pri pomoshchi sistemy trekinga // Vestnik Moskovskogo universiteta. Seriya 1: Matematika. Mekhanika. — 2014. — № 1. — S. 68–71.
5. Borodkin L. I. Tsifrovye tekhnologii v zadachakh virtual'noi rekonstruktsii istoricheskogo gorodskogo landshafta // Vestnik Permskogo universiteta. Seriya "Istoriya". — 2019. — № 3. — S. 109–117.
6. Kruchinina A. P., Latonov V. V., Chertopolokhov V. A. Obzor tekhnologii vizual'noi imitatsii v trenazhernykh sistemakh // Pilotiruemye polety v kosmos. — 2019. — № 3. — S. 89–107.
7. Fitts, Paul M. (1954). The information capacity of the human motor system in controlling the amplitude of movement. Journal of Experimental Psychology. 47 (6): 381-391.
8. Feldman, A.G. (1986). Journal of Motor Behavior, 18:17-54.
9. Kruchinina, A. P. & Yakushev, A. G. (2018). A mathematical model of optimal saccadic eye movement by a pair of muscles. Biophysics. 63 (2): 241-247.
10. Kruchinina, A.P. & Yakushev, A.G. (2019). Statistical study of the single saccade eye movement forms. Journal of Mathematical Sciences. 22 (2).
11. NASA. (July, 1995). Man-Systems Integration Standards, Revision B.
12. Bellman, R. (1957). Functional Equations in the theory of dynamic programming. Ann. Math., 65.
13. Lemak S. S. K voprosu o formirovanii pozitsionnykh strategii differentsial'noi igry v metode ekstremal'nogo pritselivaniya N.N. Krasovskogo // Vestnik Moskovskogo universiteta. Seriya 1: Matematika. Mekhanika. — 2015. — № 6. — S. 61–65.
| 















 This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

