Building models of the movement of objects in the pursuit problem and solving it in the "MathCAD" computational mathematics system

ПОСТРОЕНИЕ МОДЕЛЕЙ ДВИЖЕНИЯ ОБЪЕКТОВ В ЗАДАЧЕ ПРЕСЛЕДОВАНИЯ. РЕШЕНИЕ В СИСТЕМЕ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ «MATHCAD»

1. Введение. Постановка задачи

Рассмотрим задачу преследования на пересеченной местности, когда преследуемый объект («Кролик») и преследующий объект («Лиса») передвигаются в трехмерном пространстве с постоянными по модулю скоростями. В статье 1^[1] рассматривалась модель, когда траектория движения «Кролика» была предопределенной. То есть координаты положения «Кролика» в определенный момент являлись известными. В такой модели предлагалось то, что вектор скорости «Лисы» будет направлен на «Кролика» или на его предполагаемое положение в определенный момент времени.

В данной статье предлагаются иные модели поведения как «Кролика», так и «Лисы». В предлагаемой модели поведения «Кролика» будет производиться анализ пространственного положения «Лисы», ее скорости и в зависимости от этого будет «приниматься» решение «Кроликом» о направлении его движения. Точно такие же рассуждения можно провести и в отношении модели поведения «Лисы».

2. К выбору системы координат объекта преследования «Кролика»

В данной статье основным является то, что выбор «решения» (направление движения), следует после анализа текущего положения в динамической системе координат. В модели поведения «Кролика» предлагается выбрать динамическую локальную систему координат, где:

1. Центр локальной системы координат совпадает с текущими координатами горизонтальной проекции положения «Кролика» (рисунок 1).

𝐶𝑒𝑛𝑡𝑒𝑟⃗𝑑𝑦𝑛𝑎𝑚𝑖𝑐(𝑇)=[𝑋𝑟𝑎𝑏𝑏𝑖𝑡(𝑇)𝑌𝑟𝑎𝑏𝑏𝑖𝑡(𝑇)0] (1)

2. Ось абсцисс локальной системы координат совпадает с горизонтальной проекцией скорости «Кролика» на текущий момент времени.

𝐸⃗1(𝑇)=1√(𝑑𝑑𝑇𝑋𝑟𝑎𝑏𝑏𝑖𝑡(𝑇))2+(𝑑𝑑𝑇𝑌𝑟𝑎𝑏𝑏𝑖𝑡(𝑇))2∙[𝑑𝑑𝑇𝑋𝑟𝑎𝑏𝑏𝑖𝑡(𝑇)𝑑𝑑𝑇𝑌𝑟𝑎𝑏𝑏𝑖𝑡(𝑇)0]𝐸⃗2(𝑇)=1√(𝑑𝑑𝑇𝑋𝑟𝑎𝑏𝑏𝑖𝑡(𝑇))2+(𝑑𝑑𝑇𝑌𝑟𝑎𝑏𝑏𝑖𝑡(𝑇))2∙[−𝑑𝑑𝑇𝑌𝑟𝑎𝑏𝑏𝑖𝑡(𝑇)𝑑𝑑𝑇𝑋𝑟𝑎𝑏𝑏𝑖𝑡(𝑇)0] (2)

3. Ось ординат принадлежит горизонтальной плоскости проекций. Локальная система координат является ортогональной, соответственно ось аппликат есть продукт векторного произведения векторов и .

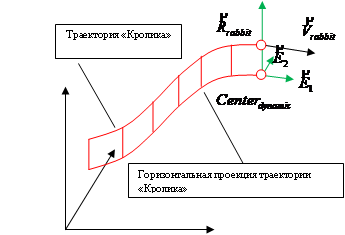
Рисунок 1- Локальная система координат "Кролика"

В нашей задаче явно выраженных зависимостей , не существует. В программе, размещенной на сайте 2^[2], для модели траектории «Кролика», приведены упорядоченные наборы точек: , , , , где – функция, описывающая ландшафт местности по точечному базису, после выполнения процедур полиномиальной регрессии и сплайн-интерполяции. Данная процедура подробно описана в комментариях к программному коду на сайте автора 2^[2], а также в статье 1^[1]. Далее, для построения функциональной зависимости траектории «Кролика» от времени T, введен формальный параметр 𝑡, 𝑡𝑖=𝑖, 𝑖∈[0..𝑁]. Из формулы для сегмента длины дуги 𝑑𝑆2=𝑑𝑋𝑟𝑎𝑏𝑏𝑖𝑡2+𝑑𝑌𝑟𝑎𝑏𝑏𝑖𝑡2+𝑑𝑍𝑟𝑎𝑏𝑏𝑖𝑡2 имеем следующее: 𝑑𝑡𝑑𝑆=1√(𝑑𝑑𝑡𝑋𝑟𝑎𝑏𝑏𝑖𝑡(𝑡))2+(𝑑𝑑𝑡𝑌𝑟𝑎𝑏𝑏𝑖𝑡(𝑡))2+(𝑑𝑑𝑡𝑍𝑟𝑎𝑏𝑏𝑖𝑡(𝑡))2.

Встроенный решатель систем обыкновенных дифференциальных уравнений системы «MathCAD» позволяет нам решить указанное дифференциальное уравнение в виде определения зависимости . Учитывая то, что мы рассматриваем случай движения с постоянной по модулю скоростью , введем в расчеты реальное время , . В расчетах нам понадобятся зависимости , , . Построение таких зависимостей указано в комментариях к программному коду на сайте автора 2^[2], 3^[3]. Учитывая все, приведенные выше условия, находим производные по времени координатных функций «Кролика». В результате имеем:

Полученные формулы (3) подставляем в формулы (2), для определения нового динамического локального базиса , , . Координаты центра локальной системы координат нам также известны. Поэтому, предварительные работы по построению динамической системы координат, можно считать выполненными.

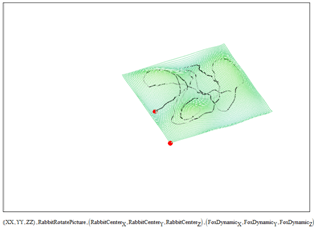
Рисунок 2 - Траектории «Лисы», «Кролика» в динамической системе координат «Кролика» (видео)

3. Траектория «Лисы» в динамической системе координат «Кролика»

Теперь нам нужно узнать, как будет выглядеть траектория «Лисы» на поверхности, заданной в виде . Поверхность, заданная в виде , при переходе в динамическую локальную систему координат , , с центром в точке
преобразуется согласно формулам (4) (рисунок2):

𝑅⃗𝑟𝑜𝑡(𝑇)=[(𝑅⃗𝑙𝑎𝑛𝑑(𝑇)−𝐶𝑒𝑛𝑡𝑒𝑟⃗𝑑𝑦𝑛𝑎𝑚𝑖𝑐(𝑇))∙𝐸⃗1(𝑇)(𝑅⃗𝑙𝑎𝑛𝑑(𝑇)−𝐶𝑒𝑛𝑡𝑒𝑟⃗𝑑𝑦𝑛𝑎𝑚𝑖𝑐(𝑇))∙𝐸⃗2(𝑇)(𝑅⃗𝑙𝑎𝑛𝑑(𝑇)−𝐶𝑒𝑛𝑡𝑒𝑟⃗𝑑𝑦𝑛𝑎𝑚𝑖𝑐(𝑇))∙𝐸⃗3(𝑇)] (4)

В источнике ^[5] размещено видео, где можно будет посмотреть динамически меняющуюся со временем базовую поверхность из системы координат «Кролика». Также, обратим внимание на координаты текущего положения «Кролика». Как и предполагалось, абсцисса и ордината равны нулю, изменяется во времени только аппликата. В источнике ^[6] представлена картина преследования «Лисой». Для дальнейшей работы, нам необходимо будет увидеть картину преследования на плоскости, в горизонтальной проекции. В источнике ^[7] представлено анимированное изображение, как в динамической системе координат, так и в мировой. На рисунке 3 представлен скриншот картины преследования на горизонтальной плоскости проекций в мировой системе координат.

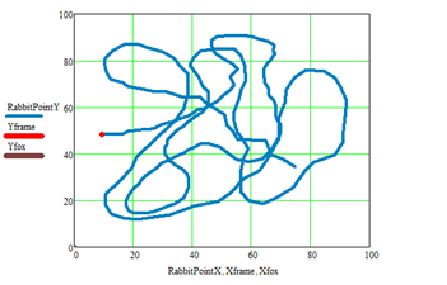
Рисунок 3 - Преследование в МСК. Горизонтальная плоскость проекций

На рисунке 4 представлен скриншот картины преследования уже в динамической системе координат «Кролика».

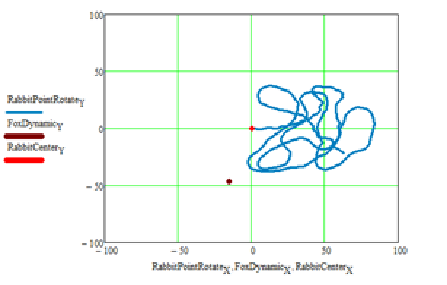
Рисунок 4 - Преследование в динамической системе координат

4. Моделирование поведения «Кролика» и «Лисы». Ситуация на плоскости

Нам сейчас необходимо рассмотреть «плоский» случай для наглядности демонстрации подхода к выбору модели движения «Кролика». Пусть «Лиса» преследует «Кролика» на плоскости. «Кролик» движется с постоянной по модулю скоростью .

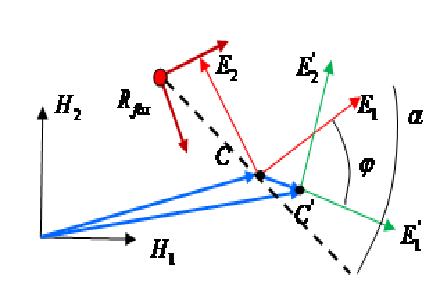
Рисунок 5 - Система координат в следующий момент времени

На рисунке 5 схематически представлена смена динамической локальной системы координат, связанной с «Кроликом», в моменты времени и . В момент времени динамическая система координат задается векторами и , а центр координат задается точкой . В момент времени система координат «кролика» переходит в положение , с центром в точке . На рисунке 5 представлена ситуация в мировой системе координат , . Далее, нам следует перейти в систему координат «Кролика» , , (рисунок 6).

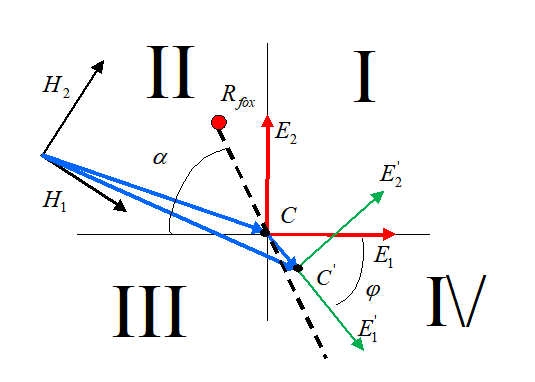
Рисунок 6 - Система координат "Кролика"

На данном рисунке 6 мы предположили, что «Лиса» приближается к «Кролику» из II четверти плоскости. Как уже предполагалось, «Кролик» расположен в точке . У нас время поделено на достаточно малые промежутки . За это время «Кролик» переходит из положения в положение : . Линия, соединяющая точки и составляет с направлением вектора угол . Но в нашей модели «Кролик» не может за промежуток времени изменить направление движения на угол . Будем считать, что угол , где - некоторое пороговое значение. Если «Кролик» будет иметь угловую скорость вращения , тогда вектор скорости повернется на угол . Мы имеем то, что в системе координат , , , координаты векторов , , будут выражены следующим образом:

𝐸⃗1′=[cos(𝜔𝑟𝑎𝑏𝑏𝑖𝑡∙∆𝑇)−sin(𝜔𝑟𝑎𝑏𝑏𝑖𝑡∙∆𝑇)]𝐸⃗2′=[𝑠𝑖𝑛(𝜔𝑟𝑎𝑏𝑏𝑖𝑡∙∆𝑇)𝑐𝑜𝑠(𝜔𝑟𝑎𝑏𝑏𝑖𝑡∙∆𝑇)]𝐶⃗′=𝑉𝑟𝑎𝑏𝑏𝑖𝑡∙∆𝑇∙[cos(𝜔𝑟𝑎𝑏𝑏𝑖𝑡∙∆𝑇)−sin(𝜔𝑟𝑎𝑏𝑏𝑖𝑡∙∆𝑇)] (5)

В мировой системе координат , вектор будет выглядеть так: . Где , базисные векторы , в системе координат , , , а , - текущие координаты «Кролика».

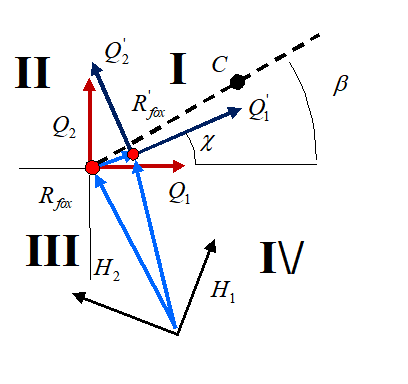
Рисунок 7 - Система координат «Лисы»

Следует пояснить, что: , , формируются текущим направлением скорости «Кролика». А компоненты векторов , после вычислений:

,где . Более детально этот момент описан на ресурсе 4^[4]. В конечном виде векторы , и новый центр координат в мировой системе координат , будут выглядеть так:

𝐶⃗𝑛𝑒𝑤=[∆𝑇∙[𝑐𝑜𝑠(𝜔𝑟𝑎𝑏𝑏𝑖𝑡∙∆𝑇)−𝑠𝑖𝑛(𝜔𝑟𝑎𝑏𝑏𝑖𝑡∙∆𝑇)]∙[𝑉𝑥−𝑉𝑦]+𝑥𝑟∆𝑇∙[𝑐𝑜𝑠(𝜔𝑟𝑎𝑏𝑏𝑖𝑡∙∆𝑇)−𝑠𝑖𝑛(𝜔𝑟𝑎𝑏𝑏𝑖𝑡∙∆𝑇)]∙[𝑉𝑦𝑉𝑥]+𝑦𝑟]𝐸⃗1𝑛𝑒𝑤=1𝑉𝑟𝑎𝑏𝑏𝑖𝑡[[𝑐𝑜𝑠(𝜔𝑟𝑎𝑏𝑏𝑖𝑡∙∆𝑇)−𝑠𝑖𝑛(𝜔𝑟𝑎𝑏𝑏𝑖𝑡∙∆𝑇)]∙[𝑉𝑥−𝑉𝑦][𝑐𝑜𝑠(𝜔𝑟𝑎𝑏𝑏𝑖𝑡∙∆𝑇)−𝑠𝑖𝑛(𝜔𝑟𝑎𝑏𝑏𝑖𝑡∙∆𝑇)]∙[𝑉𝑦𝑉𝑥]]𝐸⃗2𝑛𝑒𝑤=1𝑉𝑟𝑎𝑏𝑏𝑖𝑡[[𝑠𝑖𝑛(𝜔𝑟𝑎𝑏𝑏𝑖𝑡∙∆𝑇)𝑐𝑜𝑠(𝜔𝑟𝑎𝑏𝑏𝑖𝑡∙∆𝑇)]∙[𝑉𝑥−𝑉𝑦][𝑠𝑖𝑛(𝜔𝑟𝑎𝑏𝑏𝑖𝑡∙∆𝑇)𝑐𝑜𝑠(𝜔𝑟𝑎𝑏𝑏𝑖𝑡∙∆𝑇)]∙[𝑉𝑦𝑉𝑥]] ( (6)

Формулы (6) применимы в том случае, если «Лиса» в динамической системе координат , , приближается из II четверти (рисунок 6), при условии некоторого порогового значения.

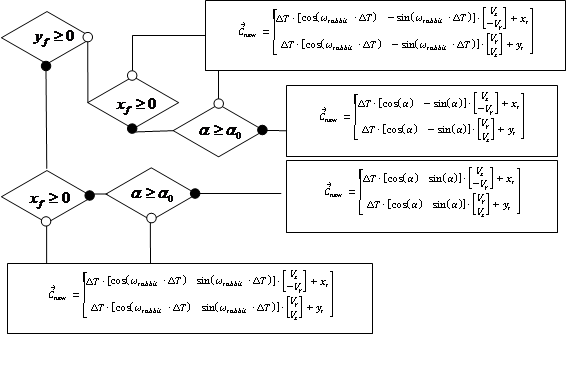
Рисунок 8 - Координаты нового центра координат в мировой системе координат

На рисунке 8 представлены возможные значения в зависимости от того из какой четверти происходит приближение «Лисы» и от значения угла .

Аналогичные рассуждения можно провести и в отношении поведения «Лисы». Сформируем систему координат , , (рисунок 7). Как и прежде, векторы базиса «Лисы» формируются ее направлением движения: , , , . В случае, показанном на рисунке (рисунок 7), в системе координат , , «Кролик» находится в Iчетверти. Линия, соединяющая «Лису» и «Кролика», составляет с вектором угол . По истечению промежутка , «Лиса» переместится на расстояние . В направлении вектора :

𝑄⃗1′=[𝑐𝑜𝑠(𝜔𝑓𝑜𝑥∙∆𝑇)𝑠𝑖𝑛(𝜔𝑓𝑜𝑥∙∆𝑇)],𝑄⃗2′=[−𝑠𝑖𝑛(𝜔𝑓𝑜𝑥∙∆𝑇)𝑐𝑜𝑠(𝜔𝑓𝑜𝑥∙∆𝑇)],𝑅⃗𝑓𝑜𝑥′=𝑣𝑓𝑜𝑥∙∆𝑇∙[𝑐𝑜𝑠(𝜔𝑓𝑜𝑥∙∆𝑇)𝑠𝑖𝑛(𝜔𝑓𝑜𝑥∙∆𝑇)] (7)

Напомним, что формулы (7) выражены в системе координат , , .

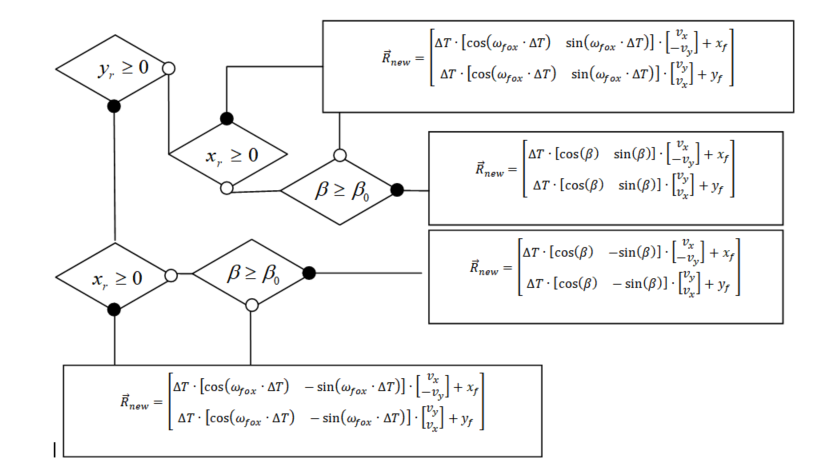
Рисунок 9 - Координаты нового положения «Лисы» в мировой системе координат

Тогда, как и в случае с «Кроликом», мы можем представить (рисунок 9) координаты нового положения «Лисы» в мировой системе координат ( - пороговое значение для угла , (рисунок 7). На рисунке 10 представлены результаты работы программы по алгоритмам, работа которых показана на рисунке 8, 9.

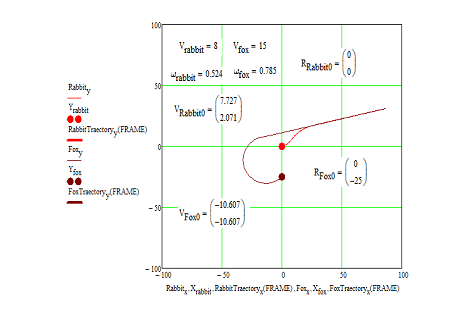
Рисунок 10 - Результаты работы программы. Моделирование на плоскости

Кроме того, мы создали плейлист ^[8], в котором частично отображена зависимость ситуации преследования от начальных данных, будь то взаимное расположение, углы направления скоростей и их абсолютные величины.

5. Модели поведения в задаче преследования на пересеченной поверхности

Мы создали модели поведения «Лисы» и «Кролика» на плоскости. Аналогичные рассуждения можно провести и в трехмерном пространстве, при моделировании задачи преследования на поверхности. Самое простое, что можно сделать, это спроецировать ход решения задачи на плоскости на поверхность, что и показывается следующем видео ^[9]. Но простая проекция с плоскости на поверхность не будет удовлетворять условиям передвижения объектов по поверхности с постоянной скоростью.

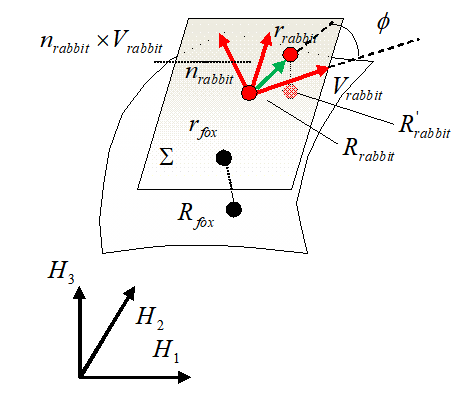
Рисунок 11 - Модель движения по поверхности («Кролик»)

Рассмотрим движение «Кролика» по поверхности. На рисунке 11 показана касательная плоскость к точке поверхности, где в определенный момент времени находится «Кролик». В данной точке вводится локальная динамическая система координат: , где - скорость «Кролика», а – нормаль к плоскости . Как и прежде, «Кролик» будет анализировать положение «Лисы», чтобы сделать следующий шаг. Для этого из точки положения «Лисы» строится ортогональная проекция на плоскость (рисунок 11). Относительно точки применяется аналогичная логика, что есть в блок-схеме, приведенной на рисунке 8. Ортогональная проекция точки положения «Лисы» на плоскость рассчитывается следующим образом:

𝑟⃗𝑓𝑜𝑥=𝑅⃗𝑓𝑜𝑥+(𝑅⃗𝑟𝑎𝑏𝑏𝑖𝑡−𝑅⃗𝑓𝑜𝑥)∙𝑛⃗𝑟𝑎𝑏𝑏𝑖𝑡𝑛⃗𝑟𝑎𝑏𝑏𝑖𝑡∙𝑛⃗𝑟𝑎𝑏𝑏𝑖𝑡∙𝑛⃗𝑟𝑎𝑏𝑏𝑖𝑡 (8)

Для того, чтобы производить анализ компонент вектора «Лисы» (8), проекцию вектора необходимо преобразовать в локальную динамическую систему координат «Кролика»:

[𝑥𝑓𝑦𝑓]=[(𝑟⃗𝑓𝑜𝑥−𝑅⃗𝑟𝑎𝑏𝑏𝑖𝑡)∙𝑉⃗𝑟𝑎𝑏𝑏𝑖𝑡[𝑉⃗𝑟𝑎𝑏𝑏𝑖𝑡](𝑟⃗𝑓𝑜𝑥−𝑅⃗𝑟𝑎𝑏𝑏𝑖𝑡)∙𝑛⃗𝑟𝑎𝑏𝑏𝑖𝑡×𝑉⃗𝑟𝑎𝑏𝑏𝑖𝑡|𝑛⃗𝑟𝑎𝑏𝑏𝑖𝑡×𝑉⃗𝑟𝑎𝑏𝑏𝑖𝑡|] (9)

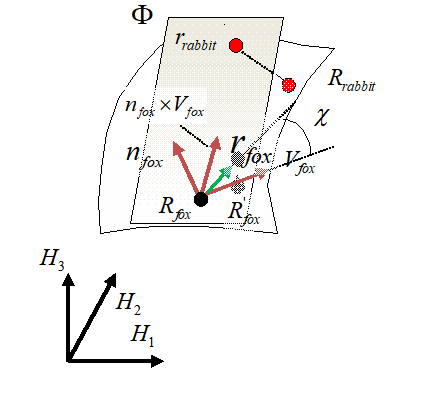
Рисунок 12 - Модель движения по поверхности («Лиса»)

После данного преобразования, мы можем произвести анализ координат по алгоритму, представленному на рисунке 8, для выбора дальнейшего движения «Кролика». Аналогичные рассуждения мы можем произвести в отношении движения «Лисы». Ортогональная проекция точки положения «Кролика» на плоскость (рисунок 12) рассчитывается так: ется так: 𝑟⃗𝑟𝑎𝑏𝑏𝑖𝑡=𝑅⃗𝑟𝑎𝑏𝑏𝑖𝑡+(𝑅⃗𝑓𝑜𝑥−𝑅⃗𝑟𝑎𝑏𝑏𝑖𝑡)∙𝑛⃗𝑓𝑜𝑥𝑛⃗𝑓𝑜𝑥∙𝑛⃗𝑓𝑜𝑥∙𝑛⃗𝑓𝑜𝑥 (10).

Проекцию положения «Кролика» (10) мы можем преобразовать в систему координат «Лисы»:

[𝑥𝑟𝑦𝑟]=[(𝑟⃗𝑟𝑎𝑏𝑏𝑖𝑡−𝑅⃗𝑓𝑜𝑥)∙𝑉⃗𝑓𝑜𝑥[𝑉⃗𝑓𝑜𝑥](𝑟⃗𝑟𝑎𝑏𝑏𝑖𝑡−𝑅⃗𝑓𝑜𝑥)∙𝑛⃗𝑓𝑜𝑥×𝑉⃗𝑓𝑜𝑥|𝑛⃗𝑓𝑜𝑥×𝑉⃗𝑓𝑜𝑥|] (11).

Проанализировать положение «Кролика» и принять соответствующее решение в отношении направления движения «Лиса» сможет согласно алгоритму, описанному на рисунке 9. На видео ^[10] можно посмотреть результат работы программы в системе «MathCAD», написанной по алгоритму, изложенному в этом параграфе.

6. Выводы

В данной статье предлагаются математические модели поведения преследующего объекта («Лисы») и преследуемого («Кролика»). Предложены модели поведения объектов на плоскости и на поверхности. Основой моделей поведения служит ввод динамических систем координат, как для «Лисы», так и для «Кролика». Системы координат формируются векторами скорости движения. Основным моментом является ввод угловой скорости вращения как «инертности» движения. Дальнейшей перспективой развития предложенных моделей нами видится ввод зависимости между угловой скоростью и скоростью движения. Другими словами, чем выше скорость, тем больше инерция. Мы считаем, что результаты, предложенные в данной статье, могут быть востребованы разработчиками автономных робототехнических комплексов, выполняющими решение задач преследования.