Retro Forecasting of Saint Petersburg Stock Exchange Indices (1914-1915): ARIMA Model Test

Фондовая торговля на Санкт-Петербургской бирже открылась в 1832 г. Ее промышленный индекс, построенный Л.И. Бородкиным и Г.Е. Перельманом ^[1] на основе помесячных цен акций 12-ти крупнейших промышленных компаний России, показывает динамику, соответствующую в целом фазам делового цикла российской промышленности с января 1897 г. по июль 1914 гг., когда в связи с началом Первой мировой войны Санкт-Петербургская биржа прекратила котировку ценных бумаг. Индекс фондовой биржи справедливо считают довольно точным индикатором экономической конъюнктуры в стране - на котировки акций влияют как внутриэкономические факторы, так и различные внешние обстоятельства, такие как, к примеру, военные действия. В период перед Первой мировой войной, начиная с 1908 г., биржевой индекс Бородкина-Перельмана показывает значительный подъем (после спада, вызванного, в основном, революцией 1905-1907 гг.). К 1912 г. индекс достигает почти своих максимальных значений, однако с 1913 г. начинается постепенное падение индекса, прерванное началом войны (рис. 1).

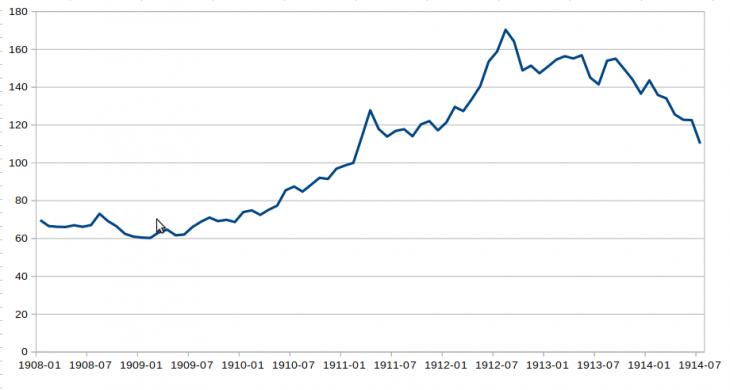
Рис. 1. Динамика индекса Санкт-Петербургской фондовой биржи в 1908-1914 гг.

Можно выдвинуть гипотезу о том, что тенденция к снижению индекса Санкт-Петербургской фондовой биржи, проявлявшаяся в течение последнего предвоенного года, имела основной причиной внутриэкономические факторы, которые должны были определять и дальнейшую динамику индекса в предположении об отсутствии войны. Есть ли основания полагать, что в рамках этой гипотезы тенденция к снижению биржевого индекса проявлялась бы и после июля 1914 г.? Иными словами, насколько оправданным можно считать предположение о том, что замедление роста индекса и постепенное снижение его значений в первой половине 1914 г. означало переход к депрессивной фазе цикла промышленного роста России? Проверку данной гипотезы предлагается осуществить с помощью контрфактической модели, прогнозирующей динамику биржевого индекса после июля 1914 г. в условиях гипотетического отсутствия войны, которая радикально изменила роль факторов довоенной динамики ^[2].

Обратимся к статистической модели ARIMA, построенной на авторегрессии временного ряда. Процесс моделирования обеспечивается программной средой R – на данный момент одной из наиболее распространенных программ для статистических исследований ^{[4, 6-8]}. К ее освоению приступила и кафедра исторической информатики исторического факультета МГУ имени М.В. Ломоносова. R является открытой, чрезвычайно гибкой и расширяемой программной средой. В ней предоставляется большой спектр статистических методов, легко расширяемых за счет библиотек различных специфических областей применения – пакетов. В частности, для создания прогноза временного ряда был использован пакет forecast, в который входит модель ARIMA.

ARIMA - это интегрированная модель авторегрессии - скользящего среднего, являющаяся расширением модели ARMA для нестационарных временных рядов. Модель ARMA используется для анализа и прогнозирования стационарных временных рядов в статистике и является обобщением двух более простых моделей временных рядов – модели авторегрессии AR и модели скользящего среднего MA. Эти модели строятся на гипотезе об авторегрессии временного ряда, взятого с заданным лагом относительно самого себя. Существует ряд публикаций, дающих представление о процессе построения модели ARIMA в программной среде R ^{[3, 5]}. Они ориентированы на работу с современными экономическими показателями, однако характеристики модели таковы, что она вполне применима и к историческим временным рядам — в соответствии с базовой гипотезой для создания модели не требуется привлечения внешних факторов, влияющих на временной ряд, так как она основана на авторегрессии.

Модель ARMA описывает стационарный ряд, который по своим характеристикам максимально приближен к «белому шуму» - во временном ряде должны отсутствовать тренд и сезонные колебания. В том случае, если исследуемый ряд имеет тренд и/или сезонные колебания, следует привести его к стационарному виду путем взятия разностей. Тренд убирается взятием разностей между последующим и предыдущим значением (вычитанием из второго значения ряда первого, из третьего второго и так далее). В том случае, если при взятии разностей все равно можно вычленить тренд, операция повторяется (из второй разности вычитается первая, из третьей вторая и так далее). Эта операция называется декомпозицией: d=1, если берется разность первого порядка, d=2, если берется разность второго порядка.

После приведения временного ряда к стационарному виду определяется порядок авторегрессии (p) и скользящей средней (q) с помощью графиков автокорреляционной функции и частной автокорреляционной функции (ACF и PACF). После этого строится регрессионное уравнение, на основании которого делается прогноз.

Для построения контрфактической модели был взят помесячный равновзвешенный индекс Санкт-Петербургской фондовой биржи, начиная с января 1908 г. и заканчивая июлем 1914 г. Эти временные рамки обусловлены окончанием спада, вызванного внешними факторами (революцией 1905 года и Русско-японской войной) и началом Первой мировой войны (и, соответственно, закрытием биржи). Таким образом, временной ряд помесячных значений биржевого индекса включает в нашем исследовании 79 точек.

Для того, чтобы определить наличие тренда и сезонного компонента была использована функция decompose(), входящей в базовый пакет R. При выведении результата в виде графика можно увидеть отдельно линию тренда и сезонные колебания (рис. 2).

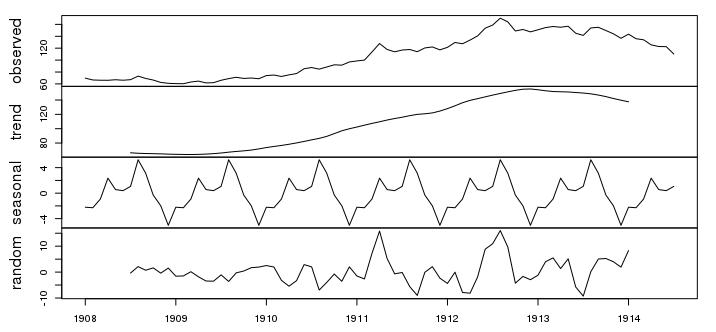
Рис. 2. Исходный ряд динамики биржевого индекса, его тренд, сезонные колебания и остатки.

На графике видно, что и тренд, и сезонные колебания заметно выражены, то есть данный временной ряд является нестационарным. Также для проверки ряда на наличие тренда был использован расширенный тест Дики-Фуллера (ADF), входящий в статистический пакет aTSA R. Тест подтвердил гипотезу о нестационарности ряда. Тогда с помощью функции diff(), входящей в статистический пакет forecast, были взяты первые разности значений исходного ряда и повторен тест ADF, который обнаружил наличие тренда и в этом ряду (рис. 3).

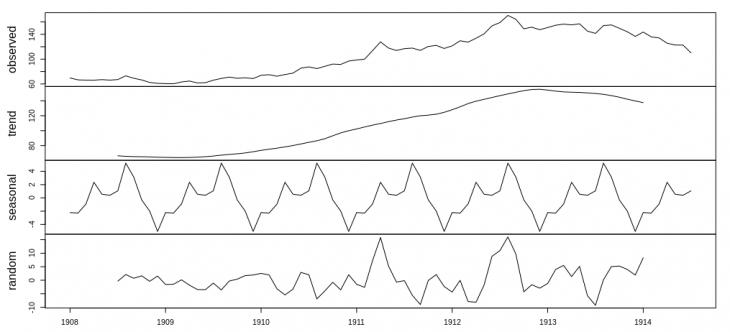
Рис. 3. Первые разности исходного ряда динамики биржевого индекса, тренд, сезонные колебания и остатки.

С учетом наблюдений из рис. 2 был сделан следующий шаг - вычисление вторых разностей (d=2). В этом случае тест ADF удостоверил наличие стационарности ряда, это же подтвеждает и рис. 4.

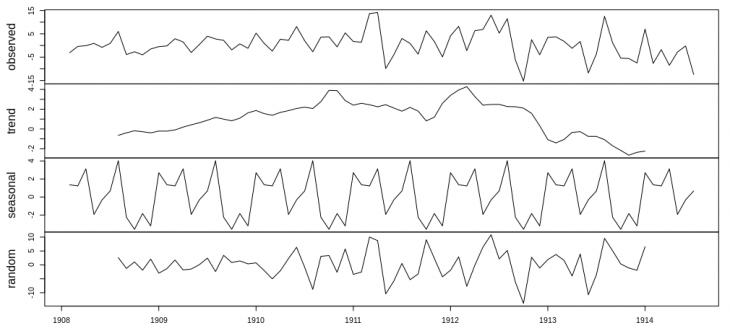
Рис. 4. Вторые разности исходного ряда динамики биржевого индекса, тренд, сезонные колебания и остатки.

Таким образом определился порядок декомпозиции, то есть параметр d в модели ARIMA. Для определения следующих параметров модели ARIMA нужно было подготовить временной ряд — убрать из него сезонную составляющую. Для этого была использована функция seasadj(), входящая в статистический пакет forecast программной среды R.

Следующим шагом стало определение оставшихся параметров — порядка авторегрессии (p) и скользящей средней (q). Для этого были построены графики автокорреляционной функции и частной автокорреляционной функции - ACF и PACF (рис. 5).

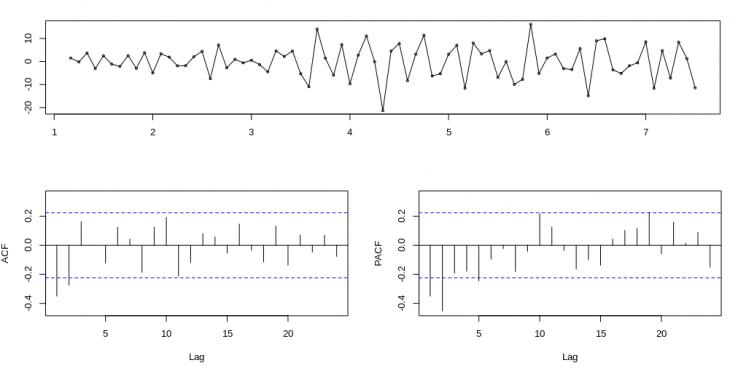
Рис. 5. Остатки временного ряда после удаления тренда и сезонных колебаний, а также две коррелограммы - автокорреляционная функция и частная автокорреляционная функция (ACF и PACF).

Автокорреляционная функция помогает определить порядок авторегрессии. График ACF показывает корреляцию временного ряда с самим собой, взятым со сдвигом во времени — лагом. Ось абсцисс показывает количество лагов, ось ординат — коэффициент корреляции, синяя линия — уровень значимости при доверительной вероятности 95%. На графике ACF мы видим два значимых значения автокорреляции — на первом и втором шагах лага, при этом в первом случае корреляция больше. Это означает, что можно пробовать в качестве параметра p значения 1 или 2, но 1 предпочтительнее.

Частная автокорреляционная функция дает представление о том, каким должен быть порядок скользящей средней. Данный график PACF показывает значимую корреляцию только на первом и втором шагах лага, но второе значение существенно превышает первое, что говорит о том, что возможен параметр q =2 в данном случае.

Надо отметить, что поиск этих двух параметров для определения оптимальной модели может оказаться довольно долгим, поскольку в основном они ищутся методом подбора наиболее вероятных вариантов.

Для начала была использована функция auto.arima(), входящая в пакет forecast R. Она, в целом, самостоятельно определяет значения p, d, и q, однако ее определения не всегда оптимальны. Оптимальность можно определить с помощью критерия Акаике (AIC) – чем меньше значение критерия, тем оптимальнее выбраны значения параметров для построения модели. Изначально была предложена модель ARIMA (0, 1, 0) – значения p и q равны нулю, а d равно единице. При такой модели критерий AIC был равен 483,07, а графики ACF и PACF показали удовлетворительный результат — ни один столбец не выходит за пределы уровня значимости (рис. 6). Если модель неверно определена, это обычно отражается на коррелограммах в виде выпадающих величин. Однако в данной модели заметна линия тренда во временном ряду — что неудивительно, так как мы уже определили, что ряд становится стационарным, если d=2.

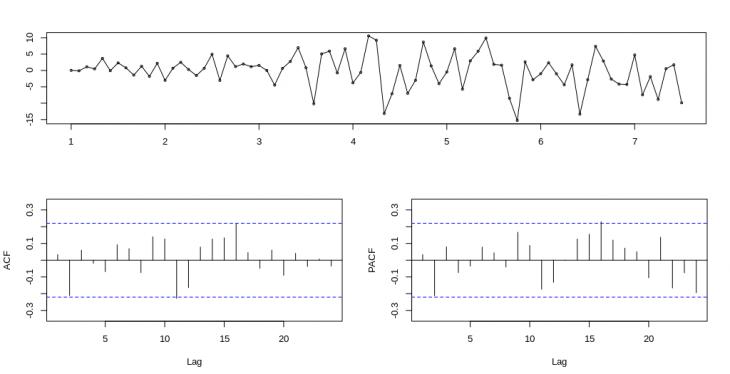
Рис. 6. Остатки временного ряда после удаления тренда и сезонных колебаний, а также две коррелограммы - автокорреляционная функция и частная автокорреляционная функция (ACF и PACF) в модели ARIMA (0, 1, 0).

В пакете forecast программной среды R есть и другая функция для построения модели ARIMA — arima(). Она позволяет самостоятельно задавать параметры модели. Задав ей параметр d=2 и путем подбора вероятных p и d, сверяя результат с критерием AIC и графиками ACF и PACF, была выбрана модель ARIMA (0, 2, 1). Ее значение критерия AIC (479,29) является оптимальным.

Итоговая модель, построенная с помощью функции forecast() сделала прогноз на последующие 12 месяцев (чем больше интервал прогнозирования, тем шире рамки доверительного интервала, поэтому было поставлено ограничение в один год). По этому прогнозу индекс продолжил бы падать и после июля 1914 г. (рис. 6) – последнее значение рассмотренного временного ряда равно 110 (июль 1914 г.), первое значение прогнозируемого, гипотетического ряда - 107 (август 1914 г.), последнее значение прогнозируемого ряда - 72 (июль 1915 г.). Однако доверительный интервал при 95% вероятности допускает и незначительный подъем индекса. На рис. 7 показаны доверительные интервалы для двух значений доверительной вероятности (90% и 95%).

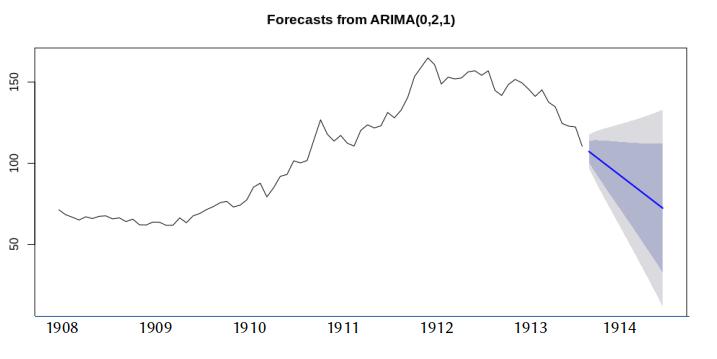
Рис. 7. Ретропрогноз динамики промышленного индекса С.-Петербургской биржи (август 1914 – июль 1915 г.): контрфактическая модель ARIMA (0, 2, 1).

Линия прогноза кажется чрезмерно упрощенной - она линейна. Напомним, что модель предполагает ряд без сезонности и тренда. Этот ретропрогноз получен на основе упрощенной авторегрессионной модели, иллюстрируя при этом процесс выбора параметров модели ARIMA в предположении о ведущей роли эндогенных (внутренних) факторов биржевой динамики.

Отметим, что аналогичную задачу по созданию контрфактической модели, характеризующей возможную динамику С.-Петербургской биржи в годы войны, решал А.В. Рачков в своей магистерской диссертации «Волатильность стоимости ценных бумаг на фондовом рынке Российской империи в 1897-1914 гг.: динамика процесса и ее факторы», защищенной в НИУ ВШЭ в 2017 г. Однако в его исследовании рассматривалась задача построения ретропрогноза другого показателя - динамики суммарной капитализации российских акционерных компаний в период с августа 1914 г. по июль 1916 г.

Построенная в данной работе контрфактическая модель показывает, что, исходя из 6-летней предвоенной динамики индекса Санкт-Петербургской биржи, в рамках гипотезы о сохранении роли влияния факторов предвоенного периода, динамика индекса в течение последующего года после июля 1914 г. проявляла бы тенденцию к понижению - даже если бы война не началась, то есть можно говорить о начале депрессивной фазы в циклическом развитии российской промышленности в течение предвоенного года.