|
DOI: 10.7256/2454-0714.2018.2.26383
Received:
23-05-2018
Published:
13-06-2018
Abstract:
The object of the study are open digital terrain models located on the Internet. The subject of the study is the procedure for eliminating the errors of digital terrain models aimed at increasing the reliability of calculations of the morphometric characteristics of basins of water bodies. This article is devoted to the improvement of methods for processing and modifying geoinformation features by processing digital high-altitude relief models. The approaches outlined in this paper are aimed at increasing the reliability of calculating the main morphometric characteristics of the relief by eliminating errors in the original data. Usually for morphometric analysis, cartographic works are used, according to which the defined relief forms contain subjective errors. The values of these errors can then affect the results of the analysis, since the quantitative characteristics depend on where and how the boundary of the form passes. Given the presence in the initial open data of a number of high-altitude distortions that indicate their inapplicability to use for qualitative morphometric analysis at the level of private watersheds, the paper considers ways to adjust their geometric characteristics by eliminating the influence of tree vegetation and preserving the relief's relief using the Lagrange coefficients. A comparison of the results of a particular morphometric analysis obtained using corrected relief models with results obtained from other data is given. To increase the reliability and automate the processing of the digital model of the river basin relief, which is a regular network, it is necessary to carry out analysis in private watersheds with an area from 0.6 to 0.8% of the total area of the basin.
Keywords:
remote sensing data, geometric modeling, normal Gaussian distribution, Lagrange interpolation polynomial, digital elevation model, forest vegetation, normalized difference vegetation index, geoinformation system, morphometric analysis, open source
Введение
В последние несколько десятилетий технические достижения в области аэрофотосъемок, дистанционного зондирования поверхности Земли и информационных технологий позволили получать цифровые изображения обширных участков территорий с высоким разрешением. В связи с этим подходы, основанные на обработке данных изображений, получили серьезный стимул для внедрения в процесс решения аналитических задач с помощью геоинформационных систем (ГИС). Цифровые модели рельефа (DEM [1]) в настоящее время широко используются при мониторинге изменений уровня воды в озерах и водохранилищах [2], определении поведения паводковых вод в бассейнах рек [3], оценке болезней сельскохозяйственных культур, определении качественных и количественных характеристик лесов [4], оценке землепользования и картирование археологических объектов и т.д. Все перечисленные приложения предполагают использование методов морфометрического анализа форм земной поверхности [5-7], основанных на классических картометрических и геометрических измерениях и преобразованиях. В то же время, точность и достоверность такого анализа в значительной степени зависит от объективности и достоверности исходных данных, из интерпретации которых в максимальной степени должны быть исключены любые посторонние погрешности, шумы и элементы субъективности.
Все методы получения основных морфометрических характеристик рельефа разработаны на базе «ручной» обработки картографических произведений [8, 9], и усовершенствованы с появлением ГИС-технологий и при этом не имеют единого технического подхода к определению, что отражено в работе Вэра об особенностях плоских топографических поверхностях (Ware J. M., A procedure for automatically correcting invalid flat trianglles occurring in triangulated countur data // Computers & Geosciences. - 1998. - 24. - Vol. 2. - P. 141-150), в исследованиях Тода, Паррата и Альвареза (Taud H., Parrot J. and Alvarez R., DEM generation by contour line dilation // Computers & Geosciences. - 1999. - 25. - P. 775-783). Установлено, что существует закономерность: чем большим преобразованиям подвергаются исходные данные о состоянии рельефа (Рисунок 1), тем больший процент погрешностей будет содержать его модель и, тем менее достоверными будут, получаемы на его основе, морфометрические характеристики. В отличие от растровых картографических материалов, цифровые данные дистанционного зондирования Земли (ДЗЗ) обладают как преимуществами (не подвержены искажениям при проецировании, не имеют погрешностей сканирования, векторизации, временных задержек и т.д.), так и недостатками (величина случайных ошибок измерений много больше, чем при наземных съёмках, в силу чего особенности морфологии частных проявлений рельефа местности часто не отражаются в полной мере). В связи с этим, на современном этапе развития, морфометрии предъявляются повышенные требования к достоверности данных о рельефе местности, повышение их точности (исключение погрешностей) и сокращение времени достижения результата.
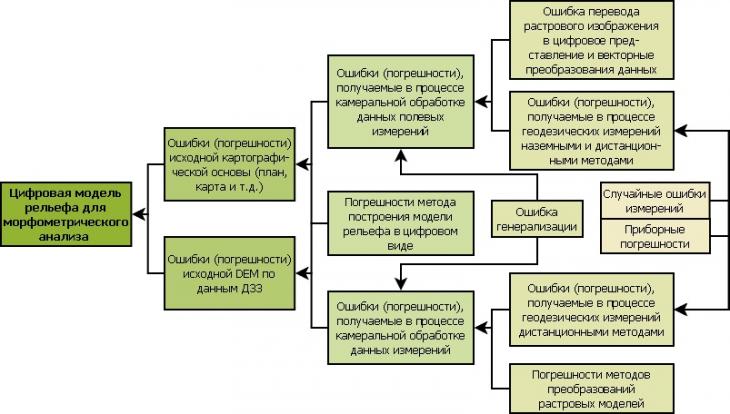
Рис. 1. Схема укрупнённых групп источников погрешностей исходных данных, влияющих на результаты морфометрического анализа по созданной ЦМР
Данная статья посвящена совершенствованию способов обработки и модификации геоинформационных признаков путем обработки цифровых высотных моделей рельефа (ЦМР). Подходы, изложенные в данной работе, направлены на повышение достоверности вычисления главных морфометрические характеристики рельефа путем устранения погрешностей в исходных данных в виде лесных массивов, строений и пр.
Место морфометрии в исследованиях рельефа бассейнов водных объекта
Морфометрический анализ как интерес к форме изучаемых объектов, благодаря использованию ГИС-технологий и всё большему накоплению данных из открытых источников, становится с каждым годом все более значимым не только для геоморфологии, но и в целом для наук о Земле. Множественность морфометрических показателей форм земной поверхности не даёт возможности непосредственно сравнить отдельные объекты в целом, из-за чего возникает необходимость выразить всю сложность топографических форм, одной количественной оценкой или морфометрической характеристикой (средняя высота, средний угол наклона, площадь топографической поверхности и объём, расчленённости и извилистость, густота эрозионной сети и т.д.). Такие характеристики тесно связаны с геометрическими особенностями поверхности рельефа территории.
Морфометрия представляет собой топографическое описание земной поверхности посредством математических законов и геометрических величин: площадей, уклонов, формы, длин и т.д. [5-9]. Эти параметры позволяют оценивать речные водосбросы в различных состояниях, включая обмеления, паводки и пр., что было отмечено в гидрологических исследованиях Джонса (Jones J. A. A., Global Hydrology: Processes, Resources and Environmental Management - Harlow : Longman, 1997. - 1 : 399 p. - ISBN 978-0-582-09861-9). Влияние этих параметров на ландшафт ранее отмечал Морисава (Morisawa M. E. Relation of Morphometric Properties to Runoff in the Little Mill Creek, Ohio Drainage Basin // Technical Report. - [s.l.] : Columbia University, Dept. of Geol., 1959. – 17 p. - Project NR 389-042.), который пришёл к выводу, что поток может быть выражен как общая функция от геоморфологии водораздела. Эта точка зрения сохраняется и в настоящее время, как отмечают Джейн и Синха (Jain V. and Sinha R. Evaluation of Geomorphic Control on Flood Hazard Through Geomorphic Instantaneous Unit Hydrograph // Research communications, Current Science. - Dec. 10, 2003. - (11) : Vol. 85. - P. 1596-1600.), Ококо и Олюджими (Okoko E. E. and Olujinmi, J. A. B. The Role of Geomorphic Features in Urban Flooding: The case of Ala River in Akure, Nigeria // Int. Journal of Environmental Issues. - 2003. - 1(1). - P. 192-201.) и Ифабии (Ifabiyi I. P. Geostudies Forum // A Reduced Rank Model of Drainage Basin Response to Runoff in Upper Kaduna Catchment of Northern Nigeria. - 2004. - P. 109-117.), которые утверждают, что геоморфологические характеристики дренажного бассейны играют ключевую роль в контроле бассейновой гидрологии. Морфометрический анализ дренажных бассейнов, таким образом, обеспечивает не только элегантное описание пейзажа, но и служит мощным средством сравнения формы и процессов водосборных бассейнов не только в пространстве, но и во времени, что было отмечено Истернбруком (Easthernbrook D. J. Surface Processes and Landforms - New York : Macmillian Publishing Co., 1993. - 325 p. - ISBN 978-0-13-860958-0.).
Ранее большинство бассейнов водных объектов описывалось либо как хорошо или плохо дренированные (осушенные), либо, согласно схеме Дэйвиса, описывались как молодые, зрелый или старый, основываясь на исследованиях Грегори и Уоллинг (Gregory K. J. and Walling D. E. Drainage Basin Form and Process: A Geomorphological Approach - London : Edward Arnold, 1973. - 456 p.). Механика того, как речные русла фактически образуются в пределах речного бассейна и как вода попадает в них, понималась геологами и гидрологами лишь в расплывчатых терминах. Измерение и количественное описание водосборного бассейна фактически внедрилось с появлением работы Джеймса Хаттона в 1775 году. Впоследствии, большой шаг вперед был сделан Хортоном в работе об исследовании бассейновых характеристик [10], где он, опираясь на предыдущие работы, добавил новые измеряемые характеристики и предложил общие методы описания параметров водосборного бассейна, которые использовались Грегори и Уоллингом. С тех пор, математический анализ водосборного бассейна широко применяется, как в умеренной зоне, что отражено в исследованиях Шумма (Schumm S. A. The Relation of Drainage Basin Relief to Sediment Loss // Internat. Assoc. Sci. Hyd. Pub.. - 1954. - 36. - P. 216-219.), Соколова (Sokolov A. A. Interrelationship between Geomorphological Characteristics of a drainage basins and the streams // Soviet Hydrology Selected Papers. - 1969. - 1. - P. 16-22.), Гардинера (Gardiner V. Technical Bulletin // Drainage Basin Morphometry. - [s.l.] : British Geomorphological Resource Group, 1975.), так и во влажных тропиках, исследованиями которых занимаются Хьюлетт и Хибберт (Hewlett J. D. and Hibbert A. R. Factor Affecting the Response of Small Watersheds to Precipitation in Humid Areas // Forest Hydrology. - [s.l.] : Pergamon, 1967. - P. 275-290.), Эбисемиджу (Ebisemiju F. S. A Reduced Rank Model of Drainage Basin Morphology // Geografiska Annaler. - 1979. - 1-2 : Vol. 16A. - P. 103-112.), Нва (Nwa E. U. Hydrologic and Physiographic Characteristics of Small, Forested Humid Tropical Watersheds // Nigerian Geographical Journal. - 1979. - (1) : Vol. 22. - 45-51 p.); Адеджувон, Джеджей и Огинкоя (Adejuwon, J. O., Jeje L. K. and Ogunkoya O. O. ydrological Response Patterns of some Third Order Streams on the Basement Comple of Southwestern Nigeria // Hydrological Science Journal. - 1984. - (3) : Vol. 28. - P. 377-391.), Рэймонд, Айандайк и Фил-Эз (Raymond N. C. Anyadike and Phillip O. Phil-Eze Runoff Response to Basin Parameters in Southeastern Nigeria // Geografiska Annaler. - [s.l.] : Taylor & Francis, Ltd, 1989. - Series A, Physical Geography. - 1/2 : Vol. 71. - P. 75-84.).
Морфометрические характеристики водосбора подвержены пространственно-временным изменениям, поэтому детальное исследование характеристик бассейна, необходимо проводить не только между разными областями, но и время от времени. Это является важным, поскольку форма бассейна в терминах его морфометрических характеристик определяет и процессы, происходящие в данном бассейне. Кроме того, все исследования рассматриваются в рамках ранжирования сети водотоков по принципу, предложенному Хортоном в работе [10] и усовершенствованном Стралером в 1957 [11], при котором численные показатели отдельно взятых бассейнов могут значительно отличаться от среднего их числа, а площади частных водосборов различаться в десятки раз и, тем самым, не давая оптимальной оценки всему бассейну.
Учитывая тесную историческую связь морфометрии с картографией, морфологией, математикой и теорией измерений, а также сильную дифференциацию между зарубежной и отечественной научными школами, сегодня все еще не существует единой стандартизированной классификации морфометрических характеристик рельефа бассейна водного объекта, что создает определенные трудности их использования для оценки территории. Однако наиболее распространенные характеристики, для определения которых разработаны наиболее объективные методы определений, структурно изложены в научных исследованиях Вахтина Б.М [5], Ефремова Ю.К. (Ефремов Ю. К. Опыт морфологической классификации элементов и простых форм рельефа // Вопросы географии. - 1949 . №11. С. 109-136) и Симонова Ю.Г. (Симонов Ю. Г. Морфометрический анализ рельефа. - Смоленск : Изд-во Смоленского гуманитарного ун-та, 1998. – 271 с). Современные методы обработки данных позволяют получать численные показатели морфометрии на любые интересующие территории, для которых создана максимально подобная действительности цифровая модель рельефа (DTM [1]).
Проблеме геометрического моделирования и математического описания ГИС (в частности для целей построения ЦМР) посвящены труды как отечественных (Павлова А.Н., Кошкарев А.В., Капралов Е.Г., Тикунов В.С., Хромых В.В., Хромых О.В, Скворцов О.В. и др.), так и зарубежных учёных (Abdul-Rahman, Alias, Pilouk, Marakot, Jarvis A., Rubiano J., Nelson A., Farrow A., Mulligan M., Tachikawa T. и др.).
Оперативно ЦМР можно получить, используя данные дистанционного зондирования Земли и последующим уточнением до максимального приближения к показателям реального рельефа местности (GMTED2010, SRTM*, Aster GDEM). Однако вопрос качества данных материалов остаётся открытым. Как уже говорилось ранее, «сырая» модель рельефа, получаемая из открытых источников, имеет большое количество артефактов, связанных с низким уровнем точности от которых зависит качество получаемых в дальнейшем результатов.
Данное обстоятельство во многих современных исследованиях не учитывается и аналитические определения, и построения различных моделей с целью определения морфометрических показателей, происходит непосредственно на «сырых» данных и несёт в себе определённые погрешности [13]. Вероятность такого отношения к материалам скорее связана с тем, что авторами исследуются большие территориальные единицы и доля ошибочно полученных данных очень мала по отношению к общему объёму.
Обработка данных ДЗЗ с целью повышения их качества
Качество и достоверность морфометрического анализа в наибольшей степени зависит от качества трехмерных моделей рельефа местности. Однако имеющиеся в сети Интернет данные ДЗЗ в большинстве случаев содержат ошибки, вызванные наличием на местности лесных массивов, возведенных строений и прочих объектов, что существенным образом влияет на точность анализа. Решение задачи, связанной с получением качественной модели рельефа связано с выявлением и частичным исключением или максимальным снижением влияния случайных ошибок (погрешностей), получаемых в процессе геодезических измерений дистанционными методами (растровые цифровые модели данных). Некоторые подходы описаны в ряде работ авторов [12-14].
Рассмотрим пути повышения качества данных ДЗЗ путем устранения влияния данных несовершенств. С этой целью растровые данные высот земной поверхности представляются в виде двумерной растровой матрицы, в которой каждый элемент несёт в себе определённую информацию. В простом случае каждая ячейка имеет одно определённое состояние или значение, в зависимости от дискретного или непрерывного пространства признаков. Более сложные случаи представляют собой матрицы с многомерными элементами. При этом местоположение, конфигурация и размеры исследуемых элементов земной поверхности, моделируются с учётом их взаимного расположения при схожих значениях или состояниях. Мозаичные модели в качестве составных частей могут включать в себя обобщённые и распределённые модели в качестве основных частей и при этом использовать любые из дифференциальных или матричных уравнений [15]. Необходимость дополнительной обработки класса ячеек матрицы, принадлежащих группе древесной растительности возникает в связи с высокой корреляцией значений максимальных погрешностей DEM в лесной зоне [12-13]. С этой целью предлагается вносить поправки, учитывающие значения смежных ячеек с введением весовой функции [13].
Для восстановления значения высот в пикселях, отнесенных к группе лесной растительности предлагается определить закон, которому подчиняется поверхность рельефа с максимальным подобием и приближением. Вес пикселя в задаваемой окрестности (может быть любой) обратно пропорционален евклидовому расстоянию между ними. При подобном распространении веса на всём окружении пикселя, величины весов каждого последующего соседствующего пикселя при приближении к краю окрестности будут стремиться к «0» (см. Рис.2). Сумма весов внутри окрестности не равна «1».
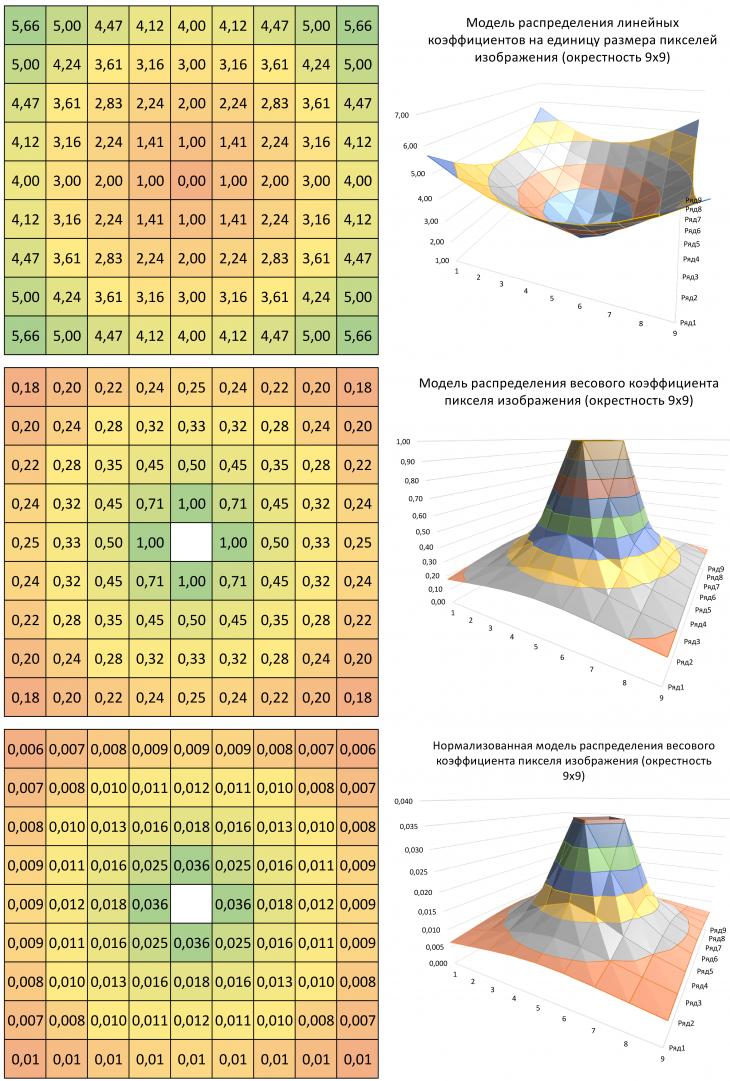
Рис. 2. Модель распределения весового коэффициента и нормализация коэффициентов модели
Пикселы, принадлежащие группе древесной растительности, не входят в обработку до момента их корректуры. После проведения процедуры перевычисления значения высоты пикселя группы древесной растительности, он используется для последующего вычисления смежный «древесных» пикселов, частные случаи перевычислений в зависимости от конфигурации, приведены на рисунке 3.
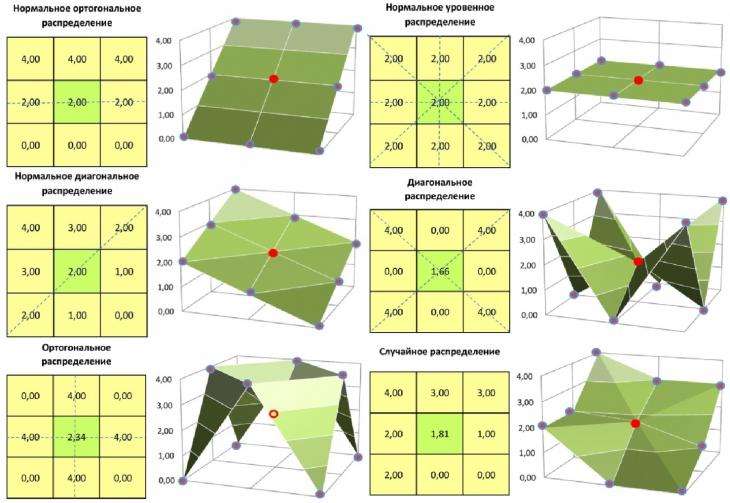
Рис. 3. Схема графического решения предлагаемого метода для определения отметки центрального пиксела (примеры по частным графическим вариациям)
Ниже, на рисунке 4 приведен пример вычисления поверхности рельефа, при наличии нескольких ячеек с лесной растительностью и сравнение данного метода с существующим алгоритмом интерполяции – IDW.
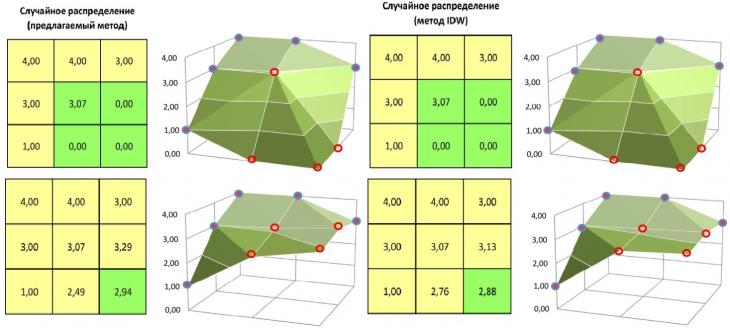
Рис. 4. Сравнение предлагаемого метода интерполяции и существующего IDW
Коэффициенты матрицы для данного метода предлагается определить методом интерполяции с применением интерполяционного полинома Лагранжа [16] необходимой степени (степень не выше 19). Расчет коэффициентов исходит из необходимого числа ячеек в матрице по каждому пикселю в отдельности (1). Предлагается использовать коэффициенты, только ограничивающие функцию при значении переменной «0».
|
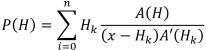 ` ` ` `
|
(1)
|
Для экспериментального подтверждения были рассмотрены два участка территории в виде регулярной матрицы высот (SRTM и ASTER GDEM приведенные к БСВ-1977 с исключением участков лесной растительности с применением метода NDVI и метода корректуры с использованием буферных зон) – {DEM} – размером 200×200 (с 90 метровым разрешением) с общим количеством ячеек с известными отметками – 40000. При больших объемах лесной растительности на выравниваемой поверхности, предлагается использование усреднённых величин значений буферных зон, выстроенных вокруг лесных массивов, т.е. весь лесной массив рассматривается как единый элемент с одинаковой поправкой за высоту древесной растительности. Для определения средней поправки (усреднённая высота деревьев) к Z-отметке участка территории, покрытого лесом, определяется разность средней отметки участка леса и средней отметки участка буферной зоны вокруг него. Участки для корректуры исходной DEM определяются по данным ДЗЗ, путём вычисления индекса NDVI (стандартизованный индекс различий растительного покрова) [17].
В процессе эксперимента каждая отметка последовательно вычислялась с использованием коэффициентов двух фильтров: нормальное гауссово распределение {kg} и предлагаемое евклидово распределение {ke} с использованием размерностей от 3×3 до 11×11 (все фильтры для простоты вычислений нормализовались таким образом, чтобы сумма участвующих в пересчете коэффициентов равнялась «1»). Затем полученные модели ([{DEM}n×{kg}={DEMg}n] и [{DEM}n×{ke}={DEMe}n]) сравнивались с исходной ([{DEMg}n-{DEM}n=Δ{DEMg}n] и [{DEMe}n-{DEM}n=Δ{DEMe}n]). В полученных матрицах поверхностей (Δ{DEMg}n и Δ{DEMe}n) проводилось взаимное сравнение отклонений и подсчет ячеек с тем или иным превышением для вычисления процентного соотношения качества перевычислений. Затем по каждому из вариантов определения вычислялись среднеквадратические погрешности с использованием формулы Гаусса (2):
|
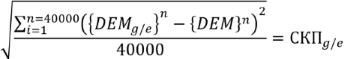
|
(2)
|
Таблица 1 – Результаты экспериментальных вычислений на {DEM}– размером 200×200 (с 90 метровым разрешением) с общим количеством ячеек с известными отметками – 40000(модели ASTER и SRTM – местность покрытая лесной растительностью на 75%, модели ASTER+и SRTM+ – местность покрытая лесной растительностью на 25%)
|
Метод
|
Процент отклонений и СКП интерполирования
|
Тип поверхности
|
|
3×3
|
5×5
|
7×7
|
9×9
|
11×11
|
|
|
Круговое распределение с использованием только функции веса
|
|
Нормальное распределение
|
77 (2,07)
|
82 (2,21)
|
87 (2,23)
|
87 (2,23)
|
87 (2,23)
|
ASTER (40000)
|
|
Евклидово распределение
|
23 (2,25)
|
18 (2,77)
|
13 (3,16)
|
13 (3,51)
|
13 (3,81)
|
|
Нормальное распределение
|
83 (1,03)
|
84 (1,23)
|
84 (1,25)
|
86 (1,25)
|
88 (1,25)
|
SRTM (40000)
|
|
Евклидово распределение
|
17 (1,22)
|
16 (1,91)
|
16 (2,44)
|
14 (2,98)
|
12 (3,53)
|
|
Нормальное распределение
|
73 (1,93)
|
74 (2,06)
|
75 (2,07)
|
76 (2,07)
|
76 (2,07)
|
ASTER+ (40000)
|
|
Евклидово распределение
|
27 (2,08)
|
26 (2,58)
|
25 (3,00)
|
24 (3,34)
|
24 (3,60)
|
|
Нормальное распределение
|
77 (1,00)
|
81 (1,19)
|
84 (1,21)
|
85 (1,21)
|
86 (1,21)
|
SRTM+ (40000)
|
|
Евклидово распределение
|
23 (1,12)
|
19 (1,82)
|
16 (2,39)
|
15 (2,93)
|
14 (3,43)
|
|
Круговое распределение с использованием коэффициентов Лагранжа и функции веса
|
|
Нормальное распределение
|
73 (2,07)
|
62 (2,21)
|
67 (2,23)
|
67 (2,23)
|
67 (2,23)
|
ASTER (40000)
|
|
Евклидово распределение
|
27 (2,08)
|
38 (2,23)
|
33 (2,38)
|
33 (2,30)
|
33 (2,30)
|
|
Нормальное распределение
|
77 (1,03)
|
64 (1,23)
|
72 (1,25)
|
73 (1,25)
|
72 (1,25)
|
SRTM (40000)
|
|
Евклидово распределение
|
23 (1,04)
|
36 (1,25)
|
28 (1,31)
|
27 (1,33)
|
28 (1,33)
|
|
Нормальное распределение
|
71 (1,93)
|
66 (2,06)
|
66 (2,07)
|
66 (2,07)
|
66 (2,07)
|
ASTER+ (40000)
|
|
Евклидово распределение
|
29 (1,93)
|
34 (2,07)
|
34 (2,11)
|
34 (2,13)
|
34 (2,12)
|
|
Нормальное распределение
|
65 (1,00)
|
66 (1,19)
|
71 (1,21)
|
71 (1,21)
|
71 (1,21)
|
SRTM+ (40000)
|
|
Евклидово распределение
|
35 (1,02)
|
34 (1,21)
|
29 (1,25)
|
29 (1,25)
|
29 (1,25)
|
|
Диагональное распределение с использованием коэффициентов Лагранжа и функции веса
|
|
Нормальное распределение
|
29 (2,07)
|
34 (2,21)
|
56 (2,23)
|
59 (2,23)
|
59 (2,23)
|
ASTER (40000)
|
|
Евклидово распределение
|
71 (2,04)
|
66 (2,19)
|
44 (2,24)
|
41 (2,26)
|
41 (2,26)
|
|
Нормальное распределение
|
27 (1,01)
|
36 (1,23)
|
65 (1,25)
|
67 (1,25)
|
68 (1,25)
|
SRTM (40000)
|
|
Евклидово распределение
|
73 (1,00)
|
64 (1,21)
|
35 (1,28)
|
33 (1,29)
|
32 (1,30)
|
|
Нормальное распределение
|
30 (1,93)
|
34 (2,06)
|
54 (2,07)
|
57 (2,07)
|
58 (2,07)
|
ASTER+ (40000)
|
|
Евклидово распределение
|
70 (1,91)
|
66 (2,04)
|
46 (2,08)
|
43 (2,09)
|
42 (2,09)
|
|
Нормальное распределение
|
31 (1,00)
|
37 (1,19)
|
51 (1,21)
|
52 (1,21)
|
57 (1,21)
|
SRTM+ (40000)
|
|
Евклидово распределение
|
69 (0,92)
|
63 (1,07)
|
49 (1,23)
|
48 (1,23)
|
43 (1,23)
|
Результатом эксперимента стало подтверждение первоначальных предположений автора, и для дальнейшей работы в морфометрическом анализе, будет использована восстановленная (исправленная, приведенная) модель рельефа SRTM+ (приведенная матрица высот к БСВ-1977 с исключением участков лесной растительности с применением метода NDVI, метода корректуры с использованием буферных зон и метода сглаживания Диагональным евклидовым распределением с использованием коэффициентов Лагранжа и функции веса).
Влияние обработки исходных данных на результаты вычисления частной морфометрии
В данном разделе приведены результаты оценки точность вычисления частных морфометрических показателей по приведенной модели рельефа на примере бассейна реки Кудьма. Определение частных морфометрических характеристик осуществлялось с использованием средств открытых систем QGIS, GRASS, GDAL и SAGA. В связи с отсутствием в морфометрии единых стандартизированных математических функций, все формулы описываются с учётом необходимых коэффициентов с применением общепринятых стандартов.
В качестве исходных данных для оценки будут использованы имеющиеся в открытом доступе данные дистанционного зондирования Земли (ДЗЗ) в виде регулярных матриц высот, полученных с использованием радиолокационных съёмок в двух вариантах – исходном («сыром») и откорректированном (метод коррекции описан выше).
Все результаты определений характеристик по моделям данных приведены в таблице 2 [18], где видны преимущества в качестве определения морфометрических характеристик бассейна водного объекта по откорректированной (выровненной) модели высот по сравнению с сырой DEM.
Таблица 2. Сводная сравнительная ведомость морфометрических характеристик
|
Характеристика
|
«Сырая» модель рельефа
|
Исправленная модель рельефа
|
Условная истинная величина показателя
|
Процент отклонения сырой/исправленной от истинной
|
Примечание
|
|
Средняя взвешенная высота бассейна, м
|
135,6
|
138,0
|
137,6
|
2 / 0
|
В картометрии применяется метод, учитывающий смежные изолинии равных высот и площади между ними, которые выступают в роли весовой функции. Для проведения сравнительного анализа были использованы открытые модули («SAGA-GIS Module Hypsometry» [19] и «Hypsometric curves» [20]) бесплатно распространяемой ГИС. Для сопоставления, величины определялась «классическим» («ручным») методом двумя способами, реализованными в стандартных функциях геометрических преобразований растровых моделей данных в ГИС MapInfo. Модуль «Raster layer statistics» [20] позволил определить среднюю величину СВБ по данным растровой цифровой модели.
|
|
Средний угол наклона бассейна
|
3 g 16 m
|
2 g 14 m
|
2 g 14 m
|
1 / 0
|
В общем случае способ определения среднего угла наклона топографической поверхности звучит следующим образом: «тангенс среднего угла наклона поверхности равен отношению суммы вертикальных площадей к сумме горизонтальных площадей ступеней ступенчатой модели» [21].
|
|
Площадь топографической поверхности, кв. км
|
3233,5
|
3231,3
|
3230,7
|
0 / 0
|
На практике площади участков территорий, вычисленные на базе моделей, заданных линиями уровней, приводятся к площадям физической (топографической) поверхности (ФП) путём введения специальных поправок. Учитывая, что ФП состоит из бесконечно большого числа малых форм расположенных относительно друг друга под разными углами и на разных высотах, площадь её определяется как сумма площадей составляющих элементов
|
|
Коэффициент горизонтальной расчлененности с учетом частных водосборов
|
0,56
|
0,68
|
0,69
|
19 / 1
|
Горизонтальное расчленение рельефа характеризуется длиной гидрографической (эрозионной) сети на квадратный километр площади. С использованием качественной модели рельефа были определены гидрографические характеристики в автоматизированном режиме с использованием модуля «r.watershed» [22]. Для сравнения с автоматизированным методом использовались данные из работы [23].
|
|
Коэффициент вертикальной расчлененности с учетом частных водосборов
|
0,40
|
0,44
|
0,46
|
13 / 4
|
Степень вертикальной расчлененности территории характеризуется глубиной расчленения рельефа. Этот показатель определяется как разность значений крайних абсолютных высот по каждому частному водосбору.
|
|
Коэффициент извилистости с учетом частных водосборов
|
1,7
|
1,4
|
1,5
|
13 / 7
|
Коэффициент извилистости принято считать, как отношение площади объекта покрытого гидрологической сетью к общей протяжённости сети.
|
Повышение достоверности путем введения расчленённости территорий
Другим способом повышения достоверности вычисления морфометрических показателей является так называемая «расчлененность» территории. Данный подход заключается в том, что морфометрические показатели вычисляются не по всей рассматриваемой территории в целом, а по отдельным участкам, что позволяет зачастую свести к минимуму погрешности вычислений. Рассмотрим данный вопрос более подробно. Определено, что при изменении площади рассматриваемой минимальной территориальной единицы коэффициент расчленённости сильно изменяется в границах своих предельных значениях, а минимальные достаточные значения площади находятся в интервале от 20 до 30 кв. км для рассматриваемого водосбора.
Из таблицы 2 видно, что показатели напрямую зависят от количественного значения высоты, и если рассматривать «сырую» высотную модель, то в ней много областей, геометрически расположенных выше, чем действительный рельеф, а в откорректированной DEM все еще имеется остаточное влияние высотных показателей древесной растительности и различных объектов естественного или искусственного происхождения, но уже в несколько раз меньшее, чем в «сырой», и, максимально приближено к условно истинным величинам, полученным ранее классическими ручными методами. Использование линейной интерполяции между полученными результатами позволяет определить оптимальное значение площади рассматриваемого частного водосбора, которое составит 22 кв. км (от 2,5 до 3 тыс. пикселов растровой модели SRTM).
При изменении площади рассматриваемой минимальной территориальной единицы коэффициент расчлененности может сильно изменяться в своих предельных значениях, а оптимальные минимальные и достаточные значения площади находятся в интервале от 5 до 10 кв.км. для рассматриваемого водосбора.
Заключение
Учитывая наличие в «сырых» открытых данных (SRTM) ряда высотных искажений, также стоит сделать заключение об их непригодности к использованию в качестве основы для выполнения качественного морфометрического анализа на уровне частных водосборов в связи с большим процентом отклонений от действительных показателей (20%), за исключением определения показателя площади физической поверхности бассейна и средней высоты водосбора. Несмотря на наличие большого числа открытых ГИС, которые позволяют проводить морфометрические характеристики, при выполнении расчётов в данной работе некоторые из открытых модулей нельзя назвать точными, в связи с чем предлагается применять ряд модулей внутри различных открытых ГИС для конкретно определённой задачи с предварительным определением условных требований и задач, предъявляемых к аналитической системе.
Из результатов, приведенных в таблице 1 можно сделать вывод о том, что: во-первых, при использовании нормального распределения, средняя ошибка интерполяции по данным модели ASTER составляет 2,1 м, в отличие от модели SRTM, где средняя ошибка интерполяции составляет 1,2 м; во-вторых, совместный диапазон отклонений нормального и евклидового распределений находится в интервале ±0,2 м в переделах конкретной модели; в-третьих, при использовании в евклидовом распределении только коэффициентов веса, качество интерполирования снижается в 2,5 – 3 раза. Таким образом, предлагаемое евклидово распределение с использованием коэффициентов Лагранжа, может быть использовано для интерполирования поверхности рельефа при ее восстановлении с применением матриц коэффициентов размерностью от 3×3 до 5×5.
На основе проведённого анализа, можно сделать заключение в части того, что ряды гидрографических характеристик водного бассейна можно подразделить на два класса: независимые абсолютные характеристики (средняя высота бассейна, средний угол наклона, среднее значение площади топографической поверхности) и весовые относительные характеристики (вертикальная и горизонтальная расчленённость, извилистость), по принципу использованных объёмов данных или её членения на области. Абсолютные характеристики не зависят от масштабного ряда принятого за основу изображения картографического произведения или пространственного разрешения цифровой модели рельефа. В работе показано, что результаты улучшаются при устранении погрешностей в исходных данных ДЗЗ, вызванных наличием на местности лесных массивов, возведенных строений и прочих объектов. Относительные характеристики напрямую зависят от масштаба анализируемого картографического произведения, особенно что касается определения гидрографических сетей и задачей генерализации сведений на картографических произведениях, следовательно, необходимым условием выполнения анализа территории бассейна водного объекта является определение минимально анализируемой площади частного водосбора. Для проведения автоматизированной обработки цифровой модели рельефа бассейна средней реки с высоким процентом достоверности необходимо проводить анализы на частных водосборах площадью от 0,6 до 0,8% от общей площади территории бассейна. Данный вывод подтверждается и в существующих методических подходах к исследованию речных бассейнов [21, 24-25]; где анализ проводится при расчленении территории на частные водосборы средней площадью в 0,7% от общей площади бассейна водного объекта.
Данное условие использования необходимого и достаточного значения площади рассматриваемых частных водосборов позволит определять весовые относительные численные морфометрические показатели бассейнов водных объектов с максимальной достоверностью, а использование открытых источников данных и свободно распространяемых ГИС ускорить процессы исследований в рамках бассейнового подход рационального природопользования и тематического картографирования бассейнов рек.
References
1. Berlyant A. M. i Koshkarev A. V. Geoinformatika. Tolkovyi slovar' osnovnykh terminov-Moskva : GIS-Assotsiatsiya, 1999. – 204 s.
2. Chang K T Introduction to Geographical Information Systems-New York : McGraw Hill, 2008.-8th Edition : 184 p.-ISBN 978-0-07-780540-1.
3. Chernikhovskii D. M. Otsenka svyazei morfometricheskikh kharakteristik rel'efa s kolichestvennymi i kachestvennymi kharakteristikami lesov na osnove tsifrovykh modelei rel'efa Aster i SRTM // Sibirskii lesnoi zhurnal.-Novosibirsk : Izdatel'stvo Sibirskogo otdeleniya RAN, 2017 g..-T. 3.-S. 28-39.-ISSN: 2311-1410 / eISSN: 2312-2099.
4. Summerfield M A Global Geomorphology-[s.l.] : Pearson Education Ltd, 1991.-Routledge; 1 edition (2 April 1991) : 537 p.-ISBN 978-0-582-30156-6.
5. Vakhtin B. M. K voprosu ob opredelenii matematicheskikh kharakteristik rel'efa mestnomsti // Geodezist.-1930 g.-2-3.
6. Sirotkin M. P. Matematicheskaya kharakteristika slozhnosti rel'efa zemnoi poverkhnosti // Geodezist.-Moskva : [b.n.], 1937. №6. S. 115-118.
7. Chentsov V. N. Morfometricheskie pokazateli rel'efa primenitel'no k geomorfologicheskim kartam // Trudy instituta geografii AN SSSR.-[b.m.] : M.-L., 1940 g. – 36 s.
8. Bobrik A. A. Geometricheskaya morfologiya sushi i okeana // (Lyubitelyam geometrii i geografii).-Sankt-Peterburg : T-vo khudozhestvennoi pechati, 1914 g. – 23 s.
9. Protod'yakonov M. M. Chislovye kharakteristiki topograficheskikh uslovii mestnosti, ischislenie ekspluatatsionnykh raskhodov i prilozhenie ikh k ekonomike zheleznykh dorog-Moskva : Transpechat', 1925. – 86 s.
10. Horton R. E. Drainage Basins Characteristics // Trans. America Geophys. Union.-1932. №13. P. 350-361.
11. Strahler A. R. Quantitative Analysis of Watershed Geomorphology // Transactions, American Geophysical Union.-Hoboken, New Jersey : John Willey & Sons, 1957.-Vol. 38 No 6.-P. 913-920.
12. Korotin A. S. i Popov E. V. GRAFIKON-2016. Trudy Mezhdunarodnoi nauchnoi konferentsii // Sozdanie tsifrovoi vysotnoi modeli s ispol'zovaniem otkrytykh dannykh distantsionnogo zondirovaniya Zemli.-2016.-S. 400-403.
13. Korotin A. S. i Popov E. V. GRAFIKON-2015. Trudy Yubileinoi 25-i Mezhdunarodnoi nauchnoi konferentsii // Otsenka tochnosti tsifrovykh modelei rel'efa, primenyaemykh dlya territorial'nykh issledovanii.-2015.-S. 102-106.
14. Markuze, Yu. I.; Bol'shakov, V. D.; Praktikum po teorii matematicheskoi obrabotki geodezicheskikh izmerenii-M. : Nedra, 1984. – 345 s.-ISBN: 978-5-903034-16-1.
15. Zamyatin A. V. i Markov N. G. Analiz dinamiki zemnoi poverkhnosti po dannym distantsionnogo zondirovaniya Zemli-M. : FIZMATLIT, 2007.-176 s.-ISBN 978-5-9221-0801-0.
16. Ignat'eva A. V., Krasnoshchekova T. I. i Smirnov V. F. Kurs vysshei matematiki-M : Vysshaya shkola, 1964.
17. Korotin A. S. 18-i Mezhdunarodnyi nauchno-promyshlennyi forum «Velikie reki’2016» // Sostavlenie tsifrovykh modelei rel'efa, primenyaemykh v basseinovykh GIS / red. Lapshin A. A.-N. Novgorod : NNGASU, 2016.-T. 1. – S. 372-373.
18. Korotin A. S. 19-i Mezhdunarodnyi nauchno-promyshlennyi forum «Velikie reki’2017» // Opredelenie optimal'noi velichiny chastnogo elementa ploshchadi vodosbora pri morfometricheskom analize rel'efa basseina vodnogo ob''ekta / red. Lapshin A. A.-N. Novgorod : NNGASU, 2017.-T. 1. – S. 390-392.
19. Conrad O. Module Hypsometry. [Elektronnyi resurs] [Elektronnyi resurs] // SAGA-GIS Module Library Documentation (v2.2.0).-2001.-http://www.saga-gis.org/saga_tool_doc/2.2.0/ta_morphometry_5.html (data obrashcheniya: 26.12.2017).
20. Raster [Elektronnyi resurs] // QGIS User Guide.-1999.-URL: https://docs.qgis.org/testing/en/docs/user_manual/processing_algs/qgis/raster_tools.html#raster-layer-statistics (data obrashcheniya: 26.12.2017).
21. Volkov N. M. Printsipy i metody kartometrii-Moskva : izd-vo AN SSSR, 1950.-329 s.
22. r.watershed-Calculates hydrological parameters and RUSLE factors. [Elektronnyi resurs] // GRASS Development Team, GRASS GIS 7.3.svn Reference Manual.-2003-2017.-URL: https://grass.osgeo.org/grass73/manuals/r.watershed.html (data obrashcheniya: 26.12.2017).
23. Korotin, A. S. 17-i mezhdunarodnyi nauchno-promyshlennyi forum «Velikie reki-2015» v 3 t. // Issledovanie sovremennoi gidrograficheskoi seti v basseine reki Kud'my s ispol'zovaniem geoinformatsionnykh sistem / red. Lapshin A. A.-N. Novgorod : Nizhegor. gos. arkhituktur.-stroit. un-t., 2016.-T. 3.-S. 456-460.
24. Beven K. J. and Moor I. D. Terrain analysis and distributed modelling in hydrology [Book].-[s.l.] : Wiley & Sons, 1993.-246 p.
25. Mozzherin V. I., Ermolaev O. P. i Mozzherin V. V. Reka Kazanka i ee bassein [Kniga].-Kazan' : izd-vo MeDDok, 2012. – 280 s
|
















 This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

