An overview of the possibilities of nonlinear deformation model in analyzing the formation and development of the nagel effect

According to modern views, based on a large experimental material ^[1], when deforming an iron-concrete element with an inclined crack in the latter, there are engagement forces and nagel forces (in the rods crossed by the crack). They are interrelated, and this seriously complicates their differentiated assessment. Nevertheless, we will try to make such an analysis. It has been experimentally established that in the reinforcing bars crossed by a crack, in addition to axial forces, transverse (nagel) forces arise ^[2]. The work of many authors is devoted to their study ^[1-15]. However, opinions on the magnitude of these forces differ significantly.

For example, Zalesov A.S. notes ^[15] that in beam elements these forces can be of considerable magnitude. Approximately the same opinion is shared by some foreign authors ^[16-17] who conducted experiments with wall models. The samples in these experiments (Fig. 1, a) were carried out in such a way as to exclude frictional forces along the cutting planes. To this end, lubricated brass sheets, paraffin interlayers, etc. were provided along these planes for these planes. These experiments showed that the value of the nagel resistance of reinforcing bars depends mainly on their diameter.

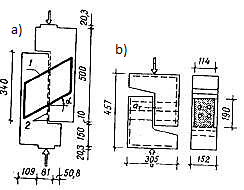
Fig. 1. Samples for studying the nagel effect (a) and the engagement forces (b) ^[15]:

1- armature; 2-brass plates coated with grease

With respect to other parameters, the opinions of the researchers differ. So, Soroushian P., Obaseki K., Rojas M.S., and Sim J. ^[16] believe that the effect of concrete strength on the strength of nagel forces is negligible, and Tassios T.P. with Vintzeleou E. ^[17] adheres to the opposite opinion. Despite the existence of experimental data confirming the essential nature of the nagel effect, many researchers ^{[3, 17, 18]} hold the view that reinforcing bars crossing the shear plane only create a compression along it, and thus cause frictional forces that, together with the engagement forces, provide joint resistance. The role of the nagel effect in the formation of this resistance, according to many of these researchers, for example, ^[3], does not exceed 1-2%. In the work, the fixed maximum of the nagel effect reached 16% of the total resistance of concrete specimens to the shear along technological seams. And it manifested itself with quite significant shear deformations along the planes, where friction, although it was eliminated to a large extent, was not entirely true. The authors of these experiments Paulay Т., Park R. and Phillips M.H. ^[18] believe that the nagel effect can not be regarded as an essential component of the resistance of reinforced concrete structures to a shift in technological seams.

Advantages of nonlinear deformation model (NDM). NDM, due to its developed functional and a wide range of modifications, can be used not only for calculating normal ^[4] and inclined cross sections ^[5], but also to generate, using the NDM, a subroutine for calculating some parameters of stress-strain state determining sections of sections. These parameters are the forces in the longitudinal working armature from the effect of the nagel effect.

The environment MathCAD has a huge set of software blocks, in which the step-iterative method for calculating the design according to NDM ^[6] is perfectly implemented. The step-iterative method allows you to simulate all the stages of loading the section of an element, to introduce parameters of non-linear properties of materials into calculation, at each stage using the modified rigidity of the structure. For example, for a stretched reinforcement at the time of the formation of the plastic hinge, the non-linearity parameter is reduced from 1 to 0, thereby reducing the flexural and shear stiffness of the reinforcing bar. When the inclined crack is opened above the permissible values, and when the steel fluidity reaches nagel, the redistribution of forces leaves the support in the span. This case is typical only for normally reinforced elements in the zone of transverse bending, with large shear spans. The zone of pure bending according to the material diagram has a large load-bearing capacity for bending, but a weak inclined section leads to the destruction of the bending element (Fig. 2).

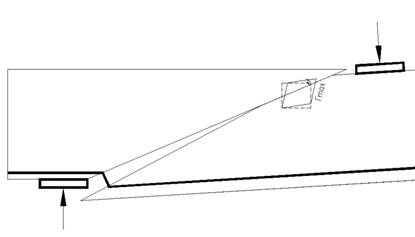
Fig. 2. Fracture of the element along the slope

The nagel effect is somewhat reduced by the action of the engagement forces along the slopes of the inclined crack, when the blocks above and below it slides against each other. In this zone, the shearing force is resisted: the transverse concrete cross section, the vertical components of the clamping forces along the length of the crack banks, and the cross-section of the reinforcing bars ^[7]. Thus, in the entire design scheme (Fig. 3), the share of the resistance of the cross-section of the rod to the shear force is not more than 2-6% of the total load. Of these, about 0-1% of the internal bending moment is perceived by the reinforcing bar, the rest of the moment is transformed into the action of normal and tangential stresses that perceive the sections of concrete and reinforcement ^{[8, 9, 10]}.

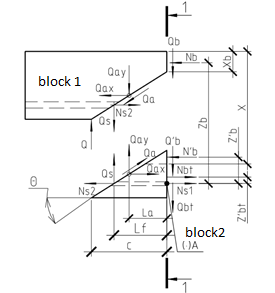
Fig. 3. To the calculation of the normal and oblique sections ^[11]

Section 1-1 (Figure 3) is the calculated normal cross-section for obtaining the missing parameters for calculating the inclined section described below. The equilibrium condition of the oblique section for one of the blocks № 1 or № 2 will be satisfied in the presence of the calculated values of equal-acting Nb and Nbt forces of normal stresses; The resultant forces Qb and Qbt of tangential stresses; Forces in the armature Ns and Qs (Qs - the nagel effect on the shift is not known); The resultant linking forces Qa. The equilibrium conditions are formed with respect to the pole "A". Where so "x" - is the value of the compressed zone; Lf, La - the shoulders of the acting forces; C - is the projection of the inclined section (assumption: the inclined crack coincides with the inclined section), `theta` - is the slope angle of the section ^[11].

This computational model (Fig. 3) fully reflects the picture of the natural work of the transverse bending zone ^[12]. As a result, the obtained SSS parameters of the inclined section ^[11] make it possible to use this model to obtain the remaining parameter of the equilibrium equation for the oblique section, namely the transverse force in the Qs armature due to the action of the nagel effect ^{[13, 14]}.

The calculation of this parameter consists in integrating the function of normal and tangential stresses along the height of the section of the stretched or compressed reinforcing bar. To perform this operation, it is necessary to break the reinforcement cross section into elementary areas within the framework of the implementation of the previous NDM units ^[20], calculate them from the flexural rigidity and proceed to the definition of normal relative deformations and stresses. The tangential stresses in the cross-section of reinforcing bars are sought by the well-known formula of the equilibrium equation of Zhuravskii ^[15], where the partial derivatives of the tangential stresses along the height of the rod section are zero. The resultant of these tangents will be the required transverse force Qs. The obtained nagel deformation model will make it possible to evaluate its SSS in the crack, taking into account the plasticity of the steel during the fracture phase, and then to determine the amount of concrete peeling along its length.

Сonclusion.

1. Since most of the formulas describing the nagel effect are empirical in nature, for example, in the work of Kani G.N.J. ^[19], this again confirms that the nature of the nagel effect has not been fully studied.

2. The results of the experiments show that, with a constant percentage of reinforcement, the ultimate breaking load for all beams is approximately the same, regardless of the diameter of the reinforcement and the strength of the steel.

3. Analysis of the research indicates that, in our opinion, a methodical error is admissible in the setting of experiments, namely: the investigated factor varies with the other conditions unchanged. In reality, there is a very flexible system of interaction of factors, which is in a state of constant change.

4. The contribution (significance) of each factor should be determined in the process of analyzing the stress-strain state, starting from the initial stress state to the boundary state.

5. A review of the research of the nagel effect in the works of foreign authors ^[16-20] showed the admissible convergence of the calculated effect of reach according to the results of the experiment ^[14].

6. Thus, the methodology of NDM for implementing this procedure is used to determine the changes that must be solved with the help of the 1st to 4th final clauses and the application of final clarity to the calculation of the strength of the inclined section.