|
DOI: 10.7256/2306-4196.2017.2.22583
Received:
05-04-2017
Published:
28-05-2017
Abstract:
The article is devoted to working out the constructive method of approximation the sum of independent random variables with the same distribution by Pearson curves. The summation theory was and still is one of the key parts of the theory of probability. The limiting theorems are proven within this theory, and they allow one to understand which frequencies may be used for the approximation for the sum so random values with large m. At the same time the approximation error is evaluated by the admissible error. However, in most practical cases the number of the summed values is not large, so the admissible error evaluation may not be sufficiently precise. The purpose of the study is to develop a constructive method for the approximation of the frequency function for the spread of the final sum of the independent random values with the same frequency. The Pearson curves are then used as approximative frequencies. Such an approximation lacks the defects related to the application of limiting theorems. It is applicable for any number of summed accidental frequencies m>1. The calculated ratios for the initial moments of the final sum of independent random variables are obtained. It is shown that the parameters of the Pearson curves for the sum m of random variables are related by simple ratios with the corresponding parameters of the summed value. The solution used in order to achieve the goal is based upon the moments method. Thе author offers a recursion formula for calculating the starting moments of for the sum of independent random values, allowing to find the central moments of the sum, as well as the parameters for the Pearson curves. It is proven that there's a dependency between the distance from the point of The exact expression for the distance from the point, corresponding to the distribution of the sum of the random variables in the coordinate system of Pearson parameters to the point (0, 3), corresponding to the normal distribution is found. By the distance value, one can indirectly assess the possibility of applying normal approximation. The author studies the possibility for the approximation of Pearson curves with normal distribution. An approximate formula for estimating the error in approximating the sum of random variables by normal distribution is given. The author provides examples of approximations for the distribution of the sum of random variables are found, which are often met in statistical radio engineering tasks. The reference materials include complete formulae for the key types of Pearson curves. All the obtained results are applicable for any random variables having finite first four initial moments. The correctness of the conclusions is confirmed by numerical calculations performed in the MathCad program.
Keywords:
random variable, Pearson curve, density function, moments of a random variable, normal distribution, sum of random variables, recursive algorithm, probability measure, approximation error, method of the moments
Введение
Исследование вероятностных характеристик сумм независимых случайных величин на протяжении длительного времени является одной из ключевых проблем теории вероятностей. И до сих пор анализу различных стохастических эффектов суммы случайных величин посвящается большое число исследований. Исторически интерес к схеме суммирования появился в связи с созданием и развитием теории ошибок измерений, когда возникло понимание, что ошибки наблюдения некоторой величины формируются под влиянием многих факторов. При этом предполагается, что вклады этих факторов в результат измерения малы и аддитивны, а сами факторы действуют независимо. В рамках этих допущений разработаны классическая и современная теории предельных теорем для сумм независимых случайных величин. Предельные теоремы указывают на возможную аппроксимацию и дают погрешность приближения в виде неравенств. Такие результаты обычно достаточны для решения практических задач, связанных с оценкой погрешности измерения. Однако существует множество задач, в которых число суммируемых величин конечно. В этом случае оценка погрешности аппроксимации оказывается недостаточно точной. Поэтому задачи с конечным числом суммируемых случайных величин решаются путем непосредственного нахождения законов распределения прямыми методами, а предельные теоремы используются в качестве подтверждения правильности полученного результата.
Известно [1, с. 89], что распределение суммы независимых случайных величин можно найти одним из следующих способов:
1) путем вычисления свертки распределений отдельных слагаемых;
2) через характеристические функции;
3) с помощью моментов.
Первые два похода дают точное решение. Однако чаще всего они сопряжены со значительными вычислительными трудностями. Исключение составляют лишь безгранично делимые распределения, перечень которых ограничен.
Метод моментов дает приближенный результат, то есть некоторую аппроксимацию распределения суммы случайных величин. Но при этом расчеты сводятся к достаточно простым вычислениям.
Аппроксимация в этом случае выполняется с помощью:
1) полиномов,
2) нормального распределения с поправками в виде полинома (метод Крамера)
или производных от нормальной плотности распределения (ряды Шарлье),
3) кривых Пирсона.
Методы Шарлье и Крамера пригодны лишь для приближенно нормальных распределений. Полиномиальная аппроксимация не имеет связи с природой случайной величины.
Метод Пирсона лишен этих недостатков. Система кривых Пирсона достаточно универсальна. Существует простой алгоритм определения типа кривой [2, с. 65]. Эти обстоятельства и определили выбор метода аппроксимации, реализованный в настоящей работе.
Целью исследования является разработка конструктивного метода аппроксимации кривыми Пирсона распределения вероятностей конечной суммы независимых одинаково распределенных случайных величин.
В ходе работы над статьей выяснилось, что, несмотря на обилие литературы, найти полное и точное описание уравнений кривых Пирсона не просто. Например, в [1, с. 133] приведены уравнения кривых, а параметры рекомендуется находить через решение вспомогательных уравнений. В других источниках ограничиваются ссылкой на результаты исследования У. Элдертона (W. Elderton), опубликованные в 1938 г. В этой связи считаем целесообразным привести точные и полные (с параметрами) уравнения кривых Пирсона основных типов.
Моменты суммы одинаково распределенных независимых случайных величин
Для определения параметров кривых Пирсона необходимо знание центральных моментов суммы случайных величин. Рассмотрим процедуру их расчета через начальные моменты.
Начальные моменты  -го порядка суммы -го порядка суммы 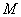 взаимно независимых случайных величин взаимно независимых случайных величин 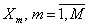 можно найти по одной из формул: можно найти по одной из формул:
 , , 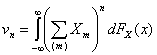 , , 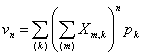 , ,
где 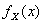 , , 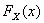 , , 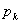 плотность, функция распределения вероятностей и закон распределения дискретной случайной величины соответственно. плотность, функция распределения вероятностей и закон распределения дискретной случайной величины соответственно.
Основная трудность, возникающая при вычислениях моментов, связана с необходимостью раскрытия суммы 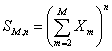 при произвольных целочисленных значениях при произвольных целочисленных значениях 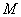 и и 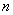 . Расчеты можно существенно упростить, если ввести рекурсивную функцию, построенную на полиномах Ньютона. Последовательно рассмотрим биномиальное представление суммы . Расчеты можно существенно упростить, если ввести рекурсивную функцию, построенную на полиномах Ньютона. Последовательно рассмотрим биномиальное представление суммы 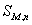 при различном числе суммируемых случайных величин. при различном числе суммируемых случайных величин.
При 
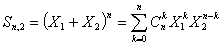 , (1) , (1)
где 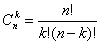 . .
При 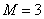
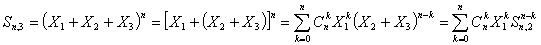 (2) (2)
В общем случае при  можно записать: можно записать:
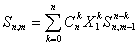 . (3) . (3)
Искомые начальные моменты суммы случайных величин найдем, усреднив выражения (1)…(3). Так, для начального момента 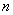 -го порядка суммы двух случайных величин получим: -го порядка суммы двух случайных величин получим:
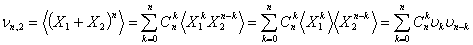 . (4) . (4)
Здесь угловыми скобками обозначена операция математического ожидания, а  - начальный момент - начальный момент 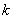 -го порядка случайной величины -го порядка случайной величины 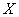 : :
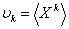 (5) (5)
Очевидно, что при 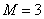 момент равен момент равен
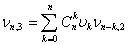 , ,
а при произвольном 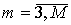 : :
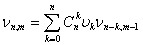 . (6) . (6)
При решении задачи аппроксимации законов распределения методом моментов, используются центральные моменты, связанные с начальными соотношением [1]:
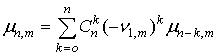 , (7) , (7)
где 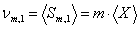 начальный момент суммы начальный момент суммы  случайных величин случайных величин 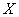 . .
В дальнейшем нам понадобятся моменты не выше четвертого порядка, которые удобней рассчитывать по развернутым формулам:
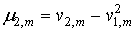 ; (8) ; (8)
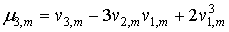 ; (9) ; (9)
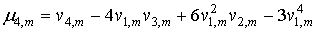 . (10) . (10)
Подставив в формулы (8…10) выражения для начальных моментов из (4) и (6) с учетом (5) получим более простые соотношения для центральных моментов суммы 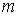 случайных величин: случайных величин:
 , (8а) , (8а)
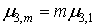 , (9а) , (9а)
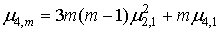 . (10а) . (10а)
Здесь 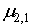 , , 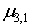 , , 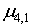 центральные моменты соответственно порядка 2, 3, 4 случайной величины центральные моменты соответственно порядка 2, 3, 4 случайной величины 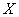 . .
Кривые Пирсона
Кривые Пирсона (распределения Пирсона) широко используются при аппроксимации распределений случайных величин. Они позволяют аппроксимировать практически все известные статистические распределения.
Пирсон предложил для описания статистического распределения случайной величины использовать решения дифференциального уравнения [3, с. 63]:
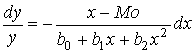 , (11) , (11)
где  – мода. – мода.
Коэффициенты в уравнении (11) могут быть вычислены с помощью центральных моментов. Они находятся из соотношений:
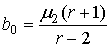 , , 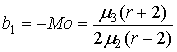 , , 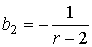
где
 . (12) . (12)
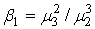 , (13) , (13)
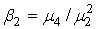 (14) (14)
Дискриминант знаменателя в уравнении (11) равен:
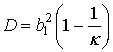 , ,
где
 (15) (15)
Общий интеграл уравнения (11) зависит от вида корней квадратного уравнения 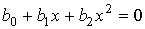 и определяется критерием и определяется критерием 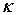 («каппа Пирсона») и дополнительными параметрами [2, с. 278]: («каппа Пирсона») и дополнительными параметрами [2, с. 278]:
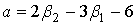 , ,
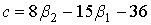 , ,
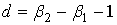 . .
В табл. 1 приведены типы кривых Пирсона и соответствующие им критерии, а так же границы области кривых Пирсона. Граница 1 – это верхняя граница всех распределений, а граница 0 – граница кривых Пирсона.
Таблица 1
|
Тип кривой
|
Граница 0
|
I
|
II
|
III
|
IV
|
V
|
VI
|
VII
|
Граница 1
|
|
Критерии
|
|
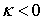
|
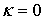
|
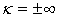
|

|
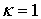
|
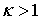
|
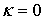
|
|
|
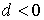
|
|

|
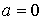
|
|
|
|
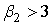
|
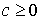
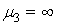
|
На рис. 1 приведен график областей кривых Пирсона, построенный по уравнениям, приведенным в [2, с. 278].
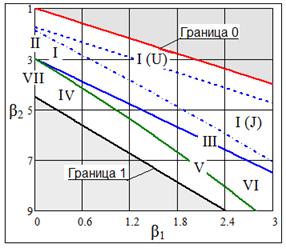
Рис. 1 График для определения типа кривой Пирсона в зависимости от  и и 
Область кривых типа I состоит из смежных областей типа I(U) (U-образные кривые плотности распределения) и типа I(J) (J-образные кривые). Точка с координатами (0;3) соответствует нормальному распределению.
Параметры и характеристики кривых Пирсона для суммы случайных величин
Найдем коэффициенты  , , 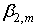 , критерий , критерий 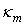 и дополнительные характеристики для суммы и дополнительные характеристики для суммы 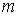 случайных величин. случайных величин.
Коэффициенты  и и 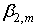 рассчитываются по формулам (13, 14), в которых центральные моменты определяются выражениями (8а…10а). Подставив соответствующие формулы (8а…10а) в (13, 14) после необходимых преобразований получим: рассчитываются по формулам (13, 14), в которых центральные моменты определяются выражениями (8а…10а). Подставив соответствующие формулы (8а…10а) в (13, 14) после необходимых преобразований получим:
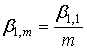 , (16) , (16)
 . (17) . (17)
Здесь 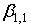 и и 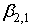 коэффициенты суммируемой случайной величины коэффициенты суммируемой случайной величины  . При известных начальных моментах . При известных начальных моментах 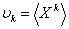 они рассчитываются по формулам: они рассчитываются по формулам:
 , ,
 , ,
где
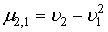 , ,
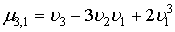 , ,
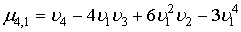 . .
Подставив в (15) выражения (16, 17) получим формулу для критерия 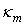 суммы суммы 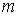 случайных величин случайных величин
 . (18) . (18)
Аналогично преобразуем формулы для дополнительных параметров:
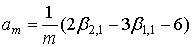 , (19) , (19)
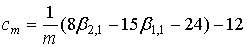 , (20) , (20)
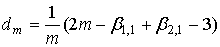 . (21) . (21)
Таким образом, коэффициенты  , ,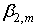 , критерий , критерий 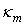 и дополнительные параметры и дополнительные параметры 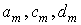 суммы независимых случайных величин определяются непосредственно через коэффициенты суммы независимых случайных величин определяются непосредственно через коэффициенты 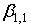 и и 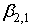 суммируемой случайной величины суммируемой случайной величины  . .
При выборе распределения обычно представляет интерес информация о том, насколько сильно аппроксимирующее распределение отличается от нормального и нельзя ли нормальное распределение использовать для аппроксимации. Косвенно о близости распределений можно судить по расстоянию в системе координат 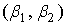 между точкой между точкой 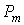 с координатами с координатами 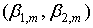 и точкой нормального распределения с координатами (0, 3). Это расстояние равно: и точкой нормального распределения с координатами (0, 3). Это расстояние равно:
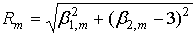
После подстановки в эту формулу выражений (16), (17) получим:
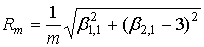 . (22) . (22)
Можно показать, что точки 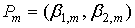 расположены на прямой, описываемой уравнением расположены на прямой, описываемой уравнением
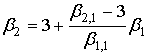 . (23) . (23)
В заключение отметим, что все расчетные соотношения этого параграфа получены для суммы независимых одинаково распределенных случайных величин и справедливы для любого исходного распределения с конечными начальными моментами 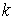 -го порядка, -го порядка, 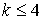 . Корректность полученных результатов подтверждается численными расчетами. Расчетные формулы весьма просты и легко реализуются в программе MathCad. . Корректность полученных результатов подтверждается численными расчетами. Расчетные формулы весьма просты и легко реализуются в программе MathCad.
На рис. 2 и 3 для примера приведены результаты расчета для суммы независимых случайных величин  с с 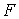 -распределением Фишера с параметрами -распределением Фишера с параметрами 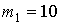 , ,  . .
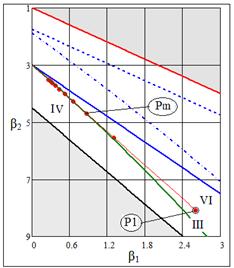
Рис. 2. Траектория точек 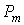 суммы суммы 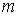 случайных величин, распределенных по закону Фишера случайных величин, распределенных по закону Фишера
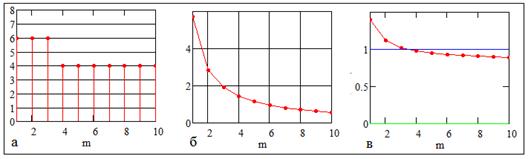
Рис. 3. Характеристики суммы случайных величин, распределенных по закону Фишера: а) зависимость типа кривой Пирсона от количества 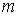 суммируемых величин; б) график расстояния суммируемых величин; б) график расстояния 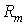 ; в) график каппы Пирсона ; в) график каппы Пирсона 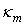 . .
Примечание. На рис. 2а номера типов кривых обозначены латинскими, а не римскими цифрами вследствие ограничений, накладываемых программой MathCad, в которой проводились расчеты.
Рисунок 2 позволяет визуально оценить тип аппроксимирующего распределения в зависимости от 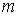 . Данные рис. 3 дают более точное представление об изменении типа распределения: при . Данные рис. 3 дают более точное представление об изменении типа распределения: при 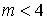 сумма аппроксимируется распределением типа VI, затем – распределением типа IV. Это подтверждается переходом критерия сумма аппроксимируется распределением типа VI, затем – распределением типа IV. Это подтверждается переходом критерия 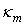 из области из области 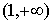 в интервал в интервал  . При этом условие . При этом условие 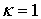 не выполняется. Следовательно, аппроксимация кривой типа III невозможна при заданных параметрах не выполняется. Следовательно, аппроксимация кривой типа III невозможна при заданных параметрах 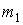 , , 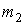 . .
Аппроксимация нормальным распределением
Функции распределения Пирсона практически всех типов выражаются через специальные функции и не табулированы. При этом квантили приходится находить численными методами. Это затрудняет решение многих прикладных задач, особенно связанных с проверкой статистических гипотез. Ситуация существенно упрощается, если в качестве аппроксимирующего распределения используется нормальное. Предпосылкой для такого решения служит тот факт, что расстояние 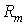 (см. (22)) с ростом (см. (22)) с ростом 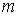 стремится к нулю, а точки стремится к нулю, а точки 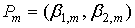 располагаются на прямой (23), начало которой находится в точке располагаются на прямой (23), начало которой находится в точке 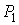 с координатами с координатами 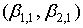 , а конец в точке (0, 3) – в точке нормального распределения (см. рис. 2). С ростом числа слагаемых , а конец в точке (0, 3) – в точке нормального распределения (см. рис. 2). С ростом числа слагаемых 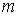 точка точка 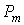 стремится к точке (0, 3), то есть к нормальному распределению. Это утверждение справедливо для суммы любых независимых одинаково распределенных случайных величин с конечными начальными моментами и является наглядной иллюстрацией справедливости центральной предельной теоремы. Отметим, что распределения Пирсона всех типов имеют конечную дисперсию, следовательно, в рассматриваемом случае выполняются условия теоремы Леви-Линдеберга [1, с. 71]. стремится к точке (0, 3), то есть к нормальному распределению. Это утверждение справедливо для суммы любых независимых одинаково распределенных случайных величин с конечными начальными моментами и является наглядной иллюстрацией справедливости центральной предельной теоремы. Отметим, что распределения Пирсона всех типов имеют конечную дисперсию, следовательно, в рассматриваемом случае выполняются условия теоремы Леви-Линдеберга [1, с. 71].
Оценка точности приближения одних случайных величин другими определяется расстоянием между ними в предварительно заданной вероятностной метрике. В настоящей работе в качестве метрики выбрано расстояние полной вариации 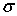 . Это «одна из самых сильных метрик, используемых в теории вероятностей» [4, с. 110]. . Это «одна из самых сильных метрик, используемых в теории вероятностей» [4, с. 110].
Привлекательность 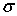 -метрики состоит еще и в том, что значения -метрики состоит еще и в том, что значения 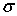 ограничены интервалом [0; 1]. При ограничены интервалом [0; 1]. При 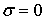 ошибки аппроксимации нет, а при ошибки аппроксимации нет, а при 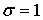 между случайными величинами существует предельно возможное различие. Тогда по величине между случайными величинами существует предельно возможное различие. Тогда по величине 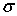 можно судить насколько сильно распределения случайных величин можно судить насколько сильно распределения случайных величин  и и 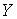 отличаются между собой по сравнению с предельно возможным случаем. отличаются между собой по сравнению с предельно возможным случаем.
Расстояние полной вариации задается соотношением:
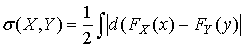 , ,
где 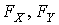 функции распределения случайных величин функции распределения случайных величин  и и 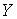 . .
В нашем случае плотности распределения существуют и 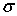 -метрику можно рассчитать по формуле -метрику можно рассчитать по формуле
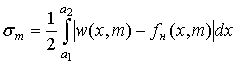 (24) (24)
Здесь 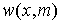 - плотность распределения суммы - плотность распределения суммы 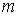 случайных величин; случайных величин; 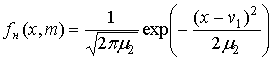 - плотность нормального распределения; - плотность нормального распределения; 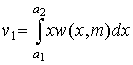 , ,  - моменты суммы - моменты суммы 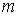 случайных величин; случайных величин; 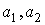 границы интервала существования плотности вероятностей границы интервала существования плотности вероятностей 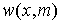 . .
Примечание. В социологии и экономике для оценки структурных сдвигов совокупностей используют дискретный аналог формулы (24), который называют индексом Лузмора-Хэнби [5].
Численные расчеты  для различных распределений суммируемой случайной величины для различных распределений суммируемой случайной величины  , показали, то выражение (24) с достаточной для практики точностью можно аппроксимировать формулой: , показали, то выражение (24) с достаточной для практики точностью можно аппроксимировать формулой:
 , (25) , (25)
где 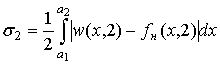 - - 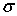 -метрика аппроксимации распределения -метрика аппроксимации распределения 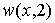 суммы двух случайных величин суммы двух случайных величин  (с исходным распределением); (с исходным распределением); 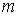 - количество суммируемых случайных величин. - количество суммируемых случайных величин.
Отметим, что выражение (25) с точностью до постоянного множителя совпадает с границей неравенства Бери-Эссеена [6, с. 155].
Некоторые плотности распределения Пирсона заданы в интервале ограниченной длины. В этом случае важным критерием качества аппроксимации является вероятность
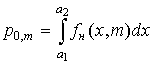 . (26) . (26)
Очевидно, что вероятность 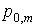 строго равна единице только при строго равна единице только при 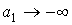 и и 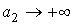 . Тем не менее, если окажется, что она достаточно близка к единице, то аппроксимацию нормальным распределением можно считать практически приемлемой, при условии, что значения . Тем не менее, если окажется, что она достаточно близка к единице, то аппроксимацию нормальным распределением можно считать практически приемлемой, при условии, что значения  малы. С другой стороны, если окажется, что вероятность малы. С другой стороны, если окажется, что вероятность  недопустимо мала, то независимо от значений недопустимо мала, то независимо от значений  от аппроксимации придется отказаться. от аппроксимации придется отказаться.
Далее приведены уравнения основных типов кривых Пирсона и примеры распределения суммы случайных величин, чаще всего встречающихся в задачах статистической радиотехники.
Кривая I типа
Ограничение: κ < 0. Уравнение:
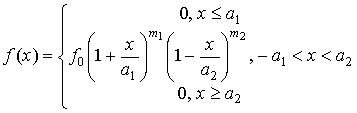 . .
Примечание. В дальнейшем для сокращения записи в формулах не указывается область нулевых значений плотности вероятности. Если приводится функция с указанием ограничений ее аргумента, то это означает, что в области, где ограничения не выполняются, функция тождественно равна нулю.
Параметры:
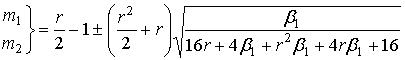 , ,
при 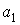 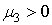 берется берется  , а при , а при 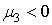  - наоборот. - наоборот.
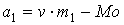 , , 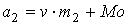 , ,
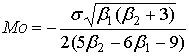
где 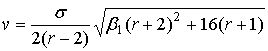 , , 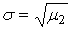 . .
Нормирующий множитель
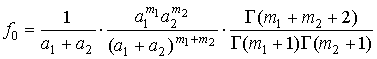 , ,
где  - гамма-функция. - гамма-функция.
Коэффициенты 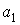 и и 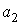 положительны. Показатели степени положительны. Показатели степени 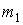 и и 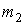 больше -1. больше -1.
Пример 1 Квадрат нормальной случайной величины
Плотность распределения [7, с. 105]:
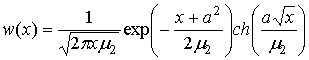 , , 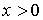 . .
Примечание. В формуле (3.10) [7, с. 105] допущена опечатка: в показателе степени экспоненты вместо y2 следует читать y.
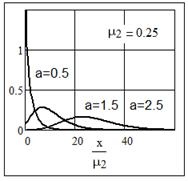
Рис. 4 Графики плотности распределения
Начальные моменты рассчитываются численно в среде MathCad:
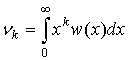 , , 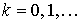
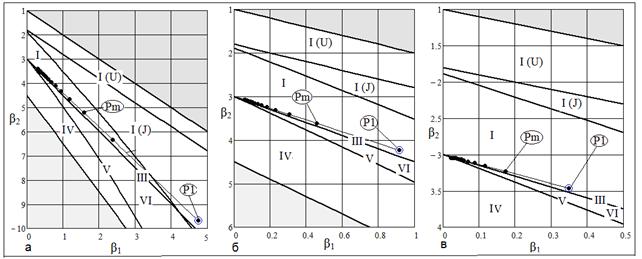
Рис. 5 Области кривых Пирсона: а) ; б) ; б)  в) в) 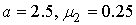
Распределение типа I. При 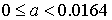 переходит в тип VI. переходит в тип VI.
Пример 2 Квадрат случайной величины с равномерным распределением
Плотность распределения можно найти по общей формуле распределения квадрата случайной величины, приведенной в [7, с. 107]. Плотность вероятностей квадрата равномерно распределенной случайной величины зависит от соотношения между границами интервала 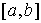 равномерного распределения: равномерного распределения:
 , , 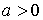 , , 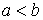 , , 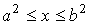 или или 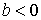 , , 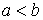 , , 
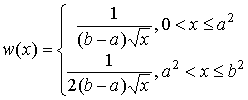 , , 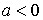 , , , , 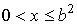 , ,
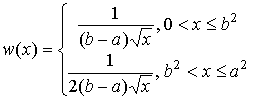 , , 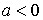 , , 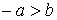 , , 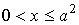 . .
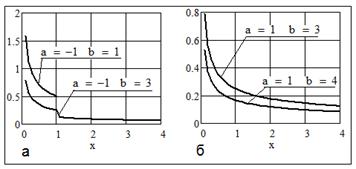
Рис. 6 Графики плотности распределения: а) 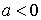 , б) , б) 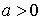
Можно показать, что начальные моменты равны:
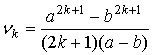 , , 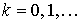
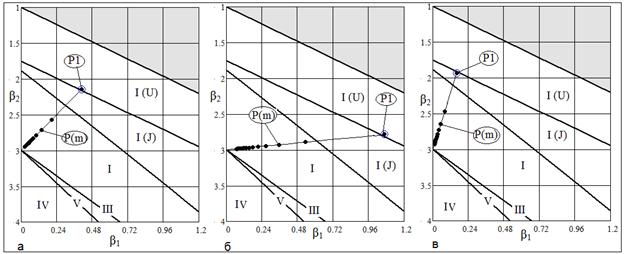
Рис. 7 Области кривых Пирсона: а)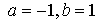 ; б) ; б)  , в) , в) 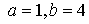
Распределение типа I(J) с переходом в I.
Пример 3 Распределение Релея
Распределение огибающей узкополосного нормального процесса.
Плотность распределения [7, с. 423]
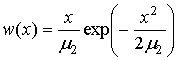 , , 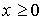 . .
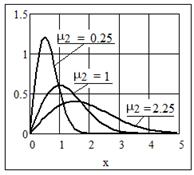
Рис. 8 Графики плотности распределения Релея
Начальные моменты [7, с. 97]
 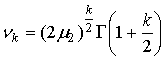 , , 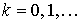
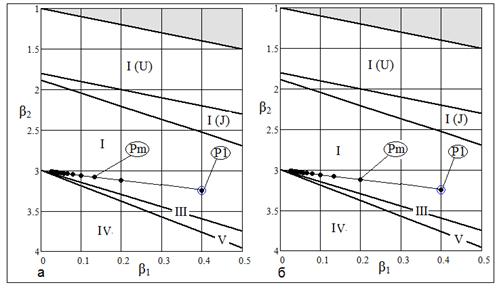
Рис. 9 Области кривых Пирсона: а) ; б) ; б) 
Распределение типа I. Параметры 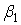 и и 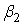 не зависят от дисперсии не зависят от дисперсии 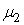 . .
Пример 4 Распределение Релея-Райса(Обобщенное распределение Релея [7, с.123])
Распределение огибающей суммы узкополосного нормального процесса и гармонического сигнала.
Плотность распределения [7, с. 121]
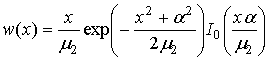 , , 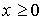 , , , ,
где 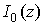 - функция Бесселя первого рода нулевого порядка. - функция Бесселя первого рода нулевого порядка.
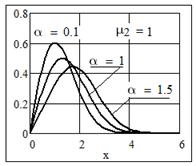
Рис. 10 Графики плотности распределения Релея-Райса
Начальные моменты [7, с. 424]
 , , 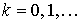 , ,
где  - вырожденная гипергеометрическая функция. - вырожденная гипергеометрическая функция.
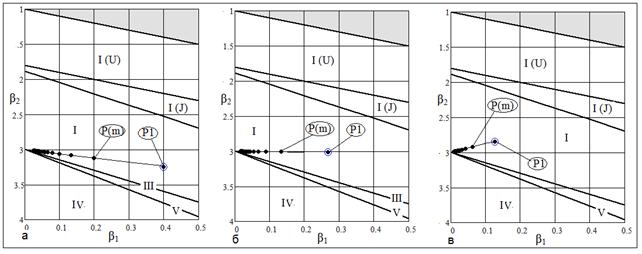
Рис. 11 Области кривых Пирсона:  , а) , а) ; б) ; б) 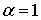 , в) , в) 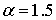
Распределение типа I.
Пример 5 Распределение Накагами (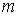 -распределение) -распределение)
Распределение огибающей гармонического сигнала со случайной амплитудой и фазой [8, с. 59].
Плотность распределения
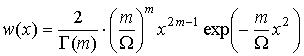 . . 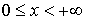 . .
Частные случаи:
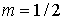 - плотность одностороннего нормального распределения; - плотность одностороннего нормального распределения;
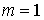 - плотность распределения Релея; - плотность распределения Релея;
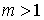 - используется для аппроксимации плотности распределения Релея-Райса. - используется для аппроксимации плотности распределения Релея-Райса.
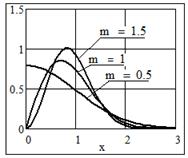
Рис. 12 Графики плотности распределения Накагами. 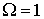
Начальные моменты
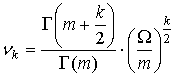 , , 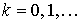
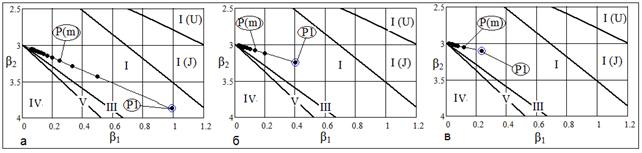
Рис. 13 Области кривых Пирсона: 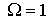 , а) , а)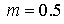 ; б) ; б)  , в) , в) 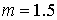
Распределение типа I.
Кривая II типа
Ограничения: 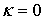 , ,  . Уравнение [3, с. 69] . Уравнение [3, с. 69]
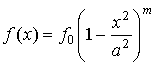 , , 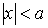 . .
Параметры:
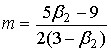 , , 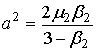 , , 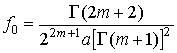 [1, с.133] [1, с.133]
Коэффициент 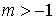 . При . При  распределение унимодальное (U-образное). распределение унимодальное (U-образное).
Пример 6 Распределение арксинуса
По закону арксинуса распределено гармоническое колебание 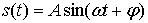 с известной амплитудой с известной амплитудой  и случайной фазой и случайной фазой 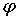 , равномерно распределенной в интервале , равномерно распределенной в интервале  . .
Плотность распределения [8, с. 184]
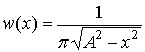 , , 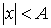 . .
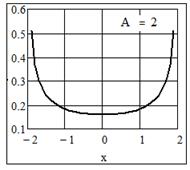
Рис. 14 График плотности распределения арксинуса
Можно показать, что первые четыре начальных момента равны
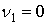 , ,  , , 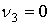 , , 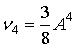 . .
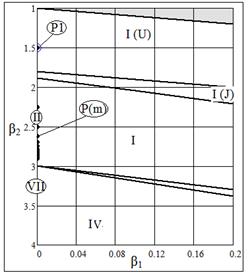
Рис. 15 Области кривых Пирсона
Сумма случайных величин аппроксимируется кривой типа II. Погрешность аппроксимации ( и и 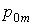 ) не зависит от параметра ) не зависит от параметра  . .
Примечание. В [9, с. 80] приведена формула для плотности распределения суммы гармонических колебаний с неодинаковыми амплитудами и случайными равномерно распределенными фазами.
Пример 7 Распределение гармонического сигнала со случайной амплитудой и фазой
Случайный сигнал 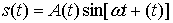 , где случайные функции , где случайные функции 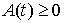 и и  независимы в один и тот же момент времени. Амплитуда независимы в один и тот же момент времени. Амплитуда 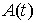 распределена равномерно в интервале распределена равномерно в интервале 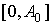 . Фаза - равномерно в интервале . Фаза - равномерно в интервале  . .
Плотность распределения мгновенного значения сигнала 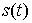 [8, с. 186]: [8, с. 186]:
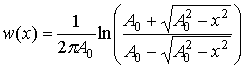 , ,  . .
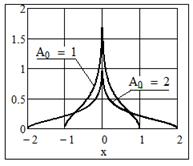
Рис. 16 Графики плотности распределения
Можно показать, что начальные моменты равны:
 , , 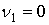 , , 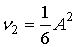 , , 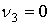 , ,  . .
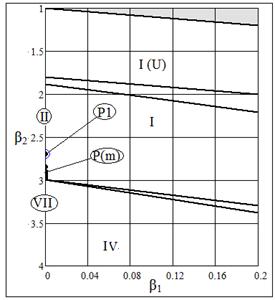
Рис. 17 Области кривых Пирсона
Погрешность аппроксимации ( и и 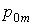 ) не зависит от параметра ) не зависит от параметра 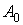 . .
Пример 8 Распределение суммы гармонического сигнала со случайной начальной фазой и нормального шума
Сумма  независимых случайных процессов: гармонического колебания независимых случайных процессов: гармонического колебания 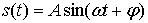 с равномерно распределенной начальной фазой и нормального стационарного шума с равномерно распределенной начальной фазой и нормального стационарного шума 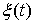 с нулевым средним и дисперсией с нулевым средним и дисперсией 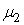
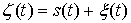 . .
Плотность распределения нормированной по 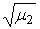 случайной величины случайной величины 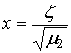 описывается формулой [8, с. 188] описывается формулой [8, с. 188]
 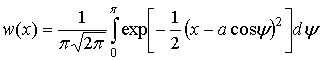 , , 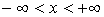 , ,
где 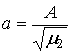 - отношение сигнал/шум по напряжению. - отношение сигнал/шум по напряжению.
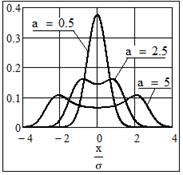
Рис. 18 Графики плотности распределения
Начальные моменты рассчитываются численно по формуле
 , , 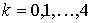 . .

Рис. 19 Области кривых Пирсона: а) 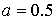 , б) , б) 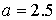 , в) , в) 
Пример 9 Равномерное распределение
Плотность распределения
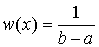 , , 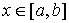 . .
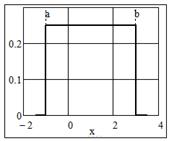
Рис. 20 График плотности равномерного распределения
Начальные моменты [1, с. 117]
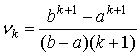 , , 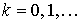
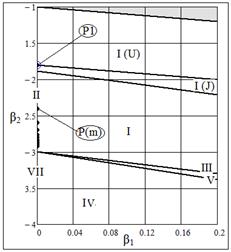
Рис. 21 Области кривых Пирсона
Погрешность аппроксимации ( и и 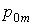 ) не зависит от параметров ) не зависит от параметров 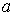 и и 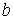 распределения. распределения.
Кривая III типа.
Ограничения: 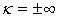 , ( , ( ). Уравнение [10, с. 286]: ). Уравнение [10, с. 286]:
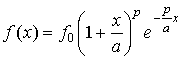 , , 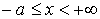 . .
Параметры:
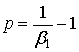 , ,  , , 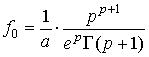 [3, с. 268]. [3, с. 268].
Мода  существует при существует при 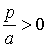 . .
Пример 10 Гамма-распределение
Плотность распределения [1, с. 121]
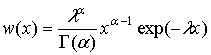 , , 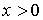 . .
Частные случаи:
при 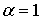 гамма-распределение совпадает с показательным; гамма-распределение совпадает с показательным;
при 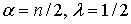 - с - с 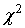 - распределением с - распределением с  степенями свободы; степенями свободы;
при 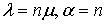 гамма-распределение называется распределением Эрланга с параметрами гамма-распределение называется распределением Эрланга с параметрами 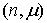 ; ;
при 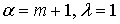 - показательно-степенное распределение с параметром - показательно-степенное распределение с параметром 
При фиксированном 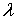 гамма-распределение является безгранично делимым. гамма-распределение является безгранично делимым.
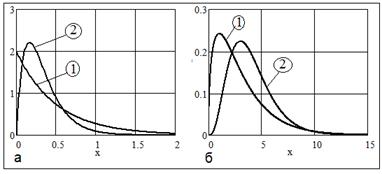
Рис. 22 Графики плотности гамма-распределения: а) 1 - показательное распределение с параметрами 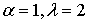 ; 2 – распределение Эрланга с параметрами ; 2 – распределение Эрланга с параметрами 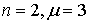 ; б) 1 – ; б) 1 – 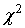 -распределение с -распределение с  степенями свободы; 2 – показательно-степенное распределение с параметрами степенями свободы; 2 – показательно-степенное распределение с параметрами 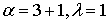
Начальные моменты [1, с. 121]:
 , , 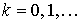
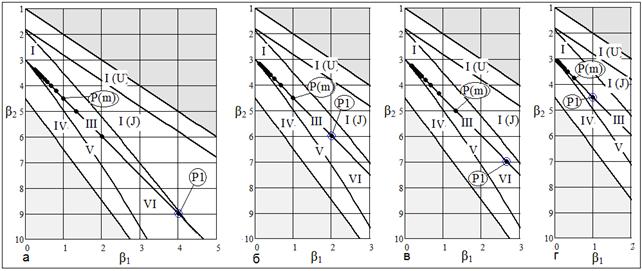
Рис. 23 Области кривых Пирсона: а) показательное распределение с параметрами 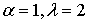 ; б) распределение Эрланга с параметрами ; б) распределение Эрланга с параметрами 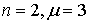 ; в) ; в)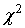 -распределение с -распределение с  степенями свободы; г) показательно-степенное распределение с параметрами степенями свободы; г) показательно-степенное распределение с параметрами 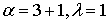 . .
Кривая IV типа
Ограничения:  , , 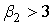 . Уравнение: . Уравнение:
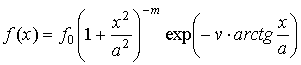 , , 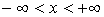 , ,
где
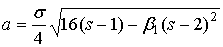 , ,  , , 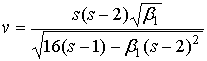 , ,
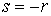 , см. формулу (12). , см. формулу (12).
Знак параметра  выбирается противоположным знаку момента выбирается противоположным знаку момента 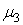 . Нормирующий множитель . Нормирующий множитель
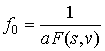 , ,
где 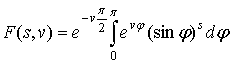 - табулированная функция. - табулированная функция.
Мода 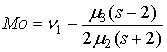 . .
Кривая V типа
Ограничение:  Уравнение: Уравнение:
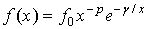 , ,  . .
Параметры
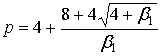 , , 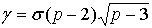 , , 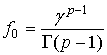 . .
Знак 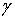 совпадает со знаком совпадает со знаком 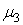 . .
Кривая VI типа
Ограничение: 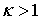 . Уравнение: . Уравнение:
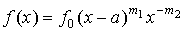 , , 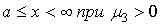 , , 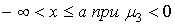 , ,
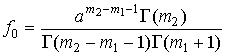 . .
Здесь
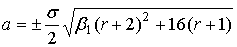 , знак совпадает со знаком , знак совпадает со знаком 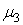 ; ;
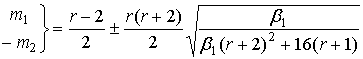 , должно выполняться неравенство , должно выполняться неравенство 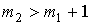 . .
Пример 11 Распределение Вейбулла
Описывает случайную наработку до отказа, при которой интенсивность отказов пропорциональна времени.
Плотность распределения
 , , 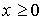 . .
Стандартная форма плотности распределения при  [8, с. 62]: [8, с. 62]:
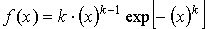 , , 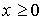 . .
Частные случаи при  : :
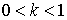 - интенсивность отказов уменьшается со временем, распределение относится к типу VI; - интенсивность отказов уменьшается со временем, распределение относится к типу VI;
 - интенсивность отказов не меняется со временем, экспоненциальное распределение (тип III); - интенсивность отказов не меняется со временем, экспоненциальное распределение (тип III);
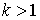 - интенсивность отказов увеличивается со временем; - интенсивность отказов увеличивается со временем;
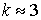 - распределение близко к нормальному; - распределение близко к нормальному;
 - распределение относится к типу VI. - распределение относится к типу VI.
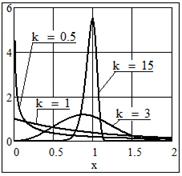
Рис. 24 Графики плотности распределения Вейбулла, 
Начальные моменты
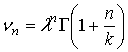 , , 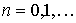
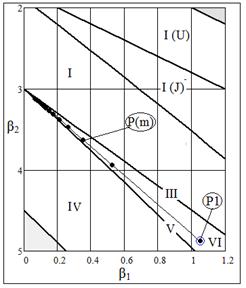
Рис. 25 Области кривых Пирсона
Распределение типа VI.
Кривая VII типа
Ограничение: 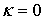 , , 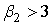 . Уравнение: . Уравнение:
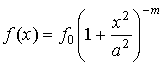 , , 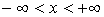 . .
Параметры:
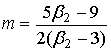 , , 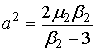 , , 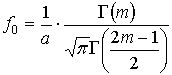 . .
Распределение симметрично относительно 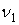 . Коэффициент . Коэффициент  . .
Заключение
Получены расчетные соотношения (4) для начальных моментов суммы независимых случайных величин.
Показано, что параметры 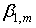 , , 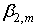 кривых Пирсона для суммы кривых Пирсона для суммы 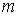 случайных величин связаны простыми соотношениями (16), (17) с соответствующими параметрами случайных величин связаны простыми соотношениями (16), (17) с соответствующими параметрами 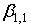 , , 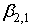 суммируемой величины. суммируемой величины.
Приведено точное выражение для расстояния 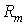 от точки, соответствующей распределению суммы случайных величин в системе координат параметров Пирсона ( от точки, соответствующей распределению суммы случайных величин в системе координат параметров Пирсона (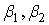 ), до точки (0, 3), соответствующей нормальному распределению. ), до точки (0, 3), соответствующей нормальному распределению.
Получена приближенная формула (25) для оценки погрешности аппроксимации суммы 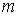 случайных величин нормальным распределением. случайных величин нормальным распределением.
Приведены точные и полные уравнения кривых Пирсона.
В качестве примеров найдены аппроксимации распределения суммы случайных величин, часто встречающихся в задачах статистической радиотехники.
Все полученные результаты применимы для любых случайных величин, имеющих конечные первые четыре начальных момента. Корректность выводов подтверждена численными расчетами.
Результаты настоящей работы могут найти применение при исследовании и проектировании каналов связи с 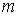 входами и общи выходом, многоканальных РЛС с ФАР, многоканальных следящих измерителей и других систем, подверженных аддитивному воздействию независимых факторов. входами и общи выходом, многоканальных РЛС с ФАР, многоканальных следящих измерителей и других систем, подверженных аддитивному воздействию независимых факторов.
References
1. Spravochnik po teorii veroyatnostei i matematicheskoi statistike/ V. S. Korolyuk, N. I. Portenko, A. V. Skorokhod, A. F. Turbin. – M.: Nauka. Gl. red. fiz.-mat. lit., 1985. – 640 s.
2. Tablitsy matematicheskoi statistki/ Bol'shev L. N., Smirnov N. V.-M.: Nauka. Gl. red. fiz.-mat. lit.. 1983. – 416 s.
3. Ryzhikov Yu. I. Upravlenie zapasami. – M.: Nauka. Gl. red. fiz.-mat. lit., – 1969.-344 s.
4. Zolotarev V. M. Sovremennaya teoriya summirovaniya nezavisimykh sluchainykh velichin. – M.: Nauka. Gl. red. fiz.-mat. lit., 1986. – 416 s.
5. Kazinets L.S. Tempy rosta i strukturnye sdvigi v ekonomike (Pokazateli planirovaniya i analiza).-M.: Ekonomika, 1981.
6. Petrov V. V. Summy nezavisimykh sluchainykh velichin. – M.: Nauka. Gl. red. fiz.-mat. lit., 1972. – 416 s.
7. Levin B. R. Teoreticheskie osnovy statisticheskoi radiotekhniki, kn. 1. – M.: Sov. radio, 1966. – 728 s.
8. Tikhonov V. I. Statisticheskaya radiotekhnika. – M.: Sov. radio, 1966. – 680 s.
9. Levin B. R. Teoreticheskie osnovy statisticheskoi radiotekhniki. – 3-e izd. pererab. i dop. – M.: Radio i svyaz', 1986. – 656 s.: il.: ISBN 5-256-00264-3.
10. Mtropol'skii A. K. Tekhnika statisticheskikh vychislenii. – M.: Nauka. Gl. red. fiz.-mat. lit., 1971.-576 s.
| 















 This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

