|
DOI: 10.7256/2306-4196.2017.2.21794
Received:
25-01-2017
Published:
28-05-2017
Abstract:
The object of study involves fuzzy logical multi-criterion methods and algorithms within the support systems for the decision making. The immediate object of study involves support systems for decision making in the sphere of dependability of technical equipment systems in the situation of fuzzy information input. The purpose of the study is to provide methodological basis for the development of applied fuzzy systems for the traditional priority studies for the multiple objects in the multi-dimensional set of quantity and quality markers based upon the linguistic statements by the experts. The article provides for the methodology of development for the support system for the decision-making in the conditions of non-precise information with the use of fuzzy theory of sets and fuzzy methods for the hierarchy analysis. The author provides detailed analysis for several aspects of the topic in question, such as application of decision-making methods for multi-criteria alternative analysis, such as the fuzzy inference and the hierarchy analysis method for fuzzy proximities. The author offers the method for ranging alternatives based upon the multi-dimensional sets of facts and criteria in the situation of fuzzy data input. The methodology of studies is based upon the formation of a model for the decision-making support system, method formalization for processing fuzzy data, algorithm development and providing for the simulation experiment for various values of managing parameters within a model. The provided methodology was implemented based upon an example of the support system for the decision-making for the expert procedure for the evaluation of general dependability of chemical technological systems. Implementation of fuzzy logic procedures when managing a complex of dependability markers is based upon the results of expert evaluation of four separate industrial objects within a single complicated technical system of oil and gas chemical production based upon five dependability criteria. Taking an example of the hierarchical structure for dependability of oil and gas equipment, the author offers a model and an algorithm for the evaluation for deriving weights with the use of a fuzzy pairwise comparison matrix based upon the judgment matrix. The experimental calculation results show that the fuzzy pairwise comparison method is efficient with greater degrees of priority fuzziness 50 to 75 percent. Efficiency of the judgment matrix depends upon the evaluation closeness or incoming linguistic values, however, it is completely dependent upon the correct formalization of data input via formation of the membership functions as well as on the formation of fuzzy rule bases. Fuzzy logical algorithms for decision making support in the sphere of managing the complex of dependability markers for the oil and gas equipment form a non-formalized part of the complex management and support systems for ensuring industrial equipment dependability. Such sub-systems allow for the preliminary evaluation of the general situation in the sphere of equipment dependability based upon the expert information.
Keywords:
equipment dependability, computer simulations, decision making, judgment matrix FAHP, deriving weights, ranking alternatives, fuzzy inference, triangular fuzzy numbers, judgment matrix, fuzzy analytic hierarchy
Введение
Принятие решений на основе показателей эффективности сложно организованных социально-технических систем на основе материальных и нематериальных показателей является более подходящим к требованиям и объектам, поскольку материальные и нематериальные показатели связаны и взаимно дополняют друг друга и определяют цели и стратегию развития системы [1, 2].
Как правило, процедуры оценивания требует учета многих факторов и критериев. Факторы могут противоречить друг другу, и альтернативы могут быть лучше или менее привлекательными при использовании различных наборов факторов. Существуют три основные особенности в решении этих задач. Во-первых, альтернативы должны быть оценены и ранжированы (полное или частичное). Во-вторых, лицо принимающее решение не может быть экспертом в области оценки альтернатив. В-третьих, в некоторых случаях фактические альтернативы могут не присутствовать в модели принятия решения.
Ранжирование альтернатив по многомерному набору факторов и критериев реализуют такие известные методы как многокритериальный метод принятия решений (Multiple Criteria Decision Analysis — MCDA) [3-5] и метод анализа иерархий (Analytic Hierarchy Process — AHP) [6, 7]. Различные вариации указанных методов используют дифференциацию информации о предпочтениях лица, принимающего решения, такую как: важность веса, порядок на критериальных шкалах, пороги для дифференциации в критериях ценностей и другие. В любом случае, общая идея методов заключается в объединение оценок всех альтернатив по всем критериям в одно значение путем построения функции, которая используется для расчета ранга альтернативы, и выбор лучшей альтернативы производится путем максимизации значения этой функции.
Основой анализа качественных показателей являются, по-прежнему, экспертные оценки. Как правило, эксперты использует при оценке каких-либо параметров знания, которые базируется скорее на отношениях между классами данных и классами гипотез, чем на отношениях между отдельными данными и конкретными гипотезами. Это имеет важное значение, и вследствие этого, лингвистические нечеткие высказывания для эксперта являются предпочтительными, чем, например, балльные оценки.
В ситуациях, когда хотя бы один из показателей альтернативы оценивается, а не измеряется, принимают, что сводное значение носит оценочный, а не точный характер. То же самое верно для промежуточных сводных показателей. Таким образом, часть показателей будет носить, четкий характер, а часть – нечеткий, независимо от числа четких показателей. Итоговый ранг будет носить нечеткий оценочный характер. Это предопределяет использование аппарата нечеткой логики для анализа систем по многомерному набору показателей, часть которых представляется нечеткими переменными. Возможно, например, перевести все четкие показатели в нечеткие значения и применить отработанные методы теории нечетких множеств для расчета итоговой оценки альтернатив. Или для решения таких задач перспективным выглядит применение методов принятия решений при многокритериальном анализе альтернатив, к которым относятся нечеткий логический вывод (НЛВ) и метод анализа иерархий (МАИ) в нечетком приближении.
Основной целью данной работы является обеспечение практиков методами нечеткой логики для традиционных исследований получения приоритета на множестве объектов по многомерному набору количественных и качественных показателей на основе лингвистических высказываний экспертов. Изложенная в статье методология реализована на примере системы поддержки принятия решений экспертной процедуры оценивания общей надежности химико-технологических систем (ХТС) с использованием нечеткой теории множеств и нечеткого метода анализа иерархий.
Нечеткий метод анализа иерархий (НМАИ) или Fuzzy Analytic Hierarchy Process (FAHP) используется для определения предпочтения оценки весов. Затем применяется процедура нечеткого логического вывода (НЛВ) или FuzzyInference System (FIS) с тем, чтобы улучшить различимость значений уровней альтернатив претендентов для каждого показателя, и на основе принятого критерия выяснить лучшие альтернативы для достижения поставленной цели.
Статья организована следующим образом. В разделах 1 и 2 представлена методология нечеткого МАИ и методология нечеткого логического вывода. Раздел 3 отображает эмпирические результаты экспертной оценки надежности четырех объектов химико-технологических систем с применением описанных методик. Обсуждения результатов и выводы приведены в разделе 4.
1 Нечеткие числа и лингвистические переменные
1.1 Определение нечеткого числа
Нечеткое множество (Fuzzy Set) представляет совокупность элементов произвольной природы, относительно которых нельзя с полной определенностью утверждать принадлежит ли тот или иной элемент рассматриваемой совокупности данному множеству или нет. В соответствии с Заде [8] нечетким множеством на универсальном множестве X называется совокупность пар:
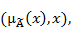
где 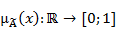 — степень принадлежности элемента — степень принадлежности элемента 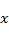 к нечеткому множеству к нечеткому множеству 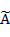 . Таким способом определена концепция частичной принадлежности элемента некоторому множеству. . Таким способом определена концепция частичной принадлежности элемента некоторому множеству.
Триангулярное (треугольное) нечеткое число (Triangular Fuzzy Numbers — TFNs) 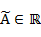 определяется триангулярной функцией принадлежности в виде [9, 10]: определяется триангулярной функцией принадлежности в виде [9, 10]:
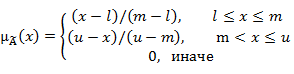
где 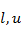 – соответственно нижняя и верхняя граница нечеткого числа – соответственно нижняя и верхняя граница нечеткого числа 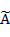 ; ; 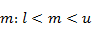 . В силу этого, нечеткое число можно задать в виде тройки . В силу этого, нечеткое число можно задать в виде тройки 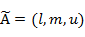 . .
Алгебраические операции сложения — 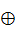 , вычитания — , вычитания — 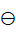 , умножения — , умножения — 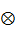 , деления — , деления — 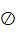 , обращения нечеткого треугольного числа — , обращения нечеткого треугольного числа — 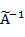 , умножения на число — , умножения на число — 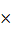 и относительное евклидово расстояние d определяют следующим образом: и относительное евклидово расстояние d определяют следующим образом:
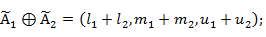
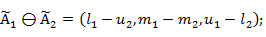
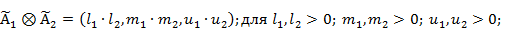
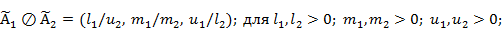
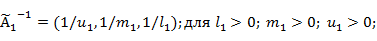
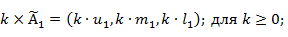
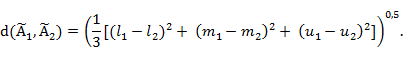
1.2 Определение лингвистической переменной
Основная цель введения лингвистических переменных — формализация нечисловых значений, задаваемых словами (фразами) естественного языка, например: «большая скорость», «высокий рост» и т.п.
Лингвистическая переменная задаётся с помощью пятёрки [9]:
{x, T(x), X, G, M},
где x– имя переменной; X – множество объектов заданного типа; T(x) – множество имен лингвистических значений переменной x; G – синтаксическое правило для образования имен значений x , порождающее новые термы с использованием квантификаторов «не», «очень», «слегка», «более-менее» и др.; M – семантическая процедура, превращающая каждый терм из G(T) в нечеткую переменную.
Например, x – «скорость»; X – множество целых чисел из диапазона (0; 300);
T(x)`supset` {«низкая», «средняя», «высокая»};
x1 = «низкая скорость»; x2 =«средняя скорость»; x3 = «высокая скорость»;
G: «очень»`cdot` y = y1 | «не очень»`cdot` y = y2,
{y, y1, y2}`subset` T(x);
M – процедура задания на X нечетких переменных, а также соответствующих нечетких множеств для термов из G(T) в соответствии с правилами трансляции нечетких связок и модификаторов.
Для заданных в примере выше нечетких переменных x1, x2, x3 процедуру М можно определить аналитически (графически, эмпирически) путем задания триангулярных функций принадлежности, а для новых термов, образованных, например, квантификатором «очень», использовать семантическое правило в виде:
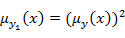 . .
2 Нечетко-логические процедуры обработки экспертной информации
Предлагается две процедуры обработки экспертной информации в условиях нечетких входных данных. Это методика анализа иерархий (МАИ), использующая нечеткие числовые оценки приоритетов в матрице парных сравнений [11-14], и методика нечеткого логического вывода (НЛВ) [15-19].
Общая схема процедуры обработки экспертной информации в условиях нечетких входных данных или модель системы поддержки принятия решения приведена на рисунке 1.
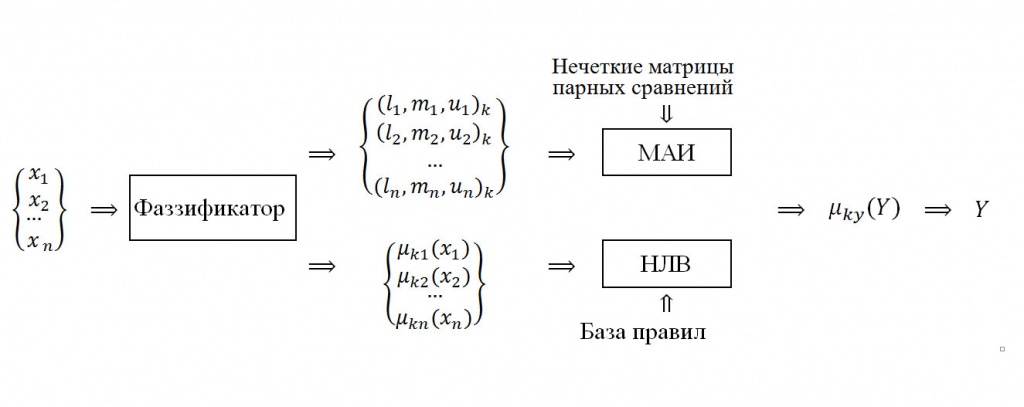
Рисунок 1 – Модель системы поддержки принятия решения в условиях нечетких входных данных
Здесь индекс k указывает на номер эксперта.
К разным группам показателей из иерархии могут применяться разные процедуры обработки экспертной информации, МАИ или НЛВ. Результаты оценок параметров модели, полученные разными методами, агрегируются в сводные значения в виде интегрированного показателя надежности.
2.1 Нечеткий метод анализа иерархий
Метод анализа иерархий (МАИ) [6, 7] является мощным методом для решения сложных задач принятия решений. МАИ широко применяется учеными и специалистами, в основном в инженерных приложениях, связанных с принятием экономически эффективных решений, при анализе атрибутов не количественного характера. Любая сложная проблема может быть разложена на несколько подзадач с использованием МАИ в терминах иерархических уровней, где каждый уровень представляет собой набор критериев или атрибутов по отношению к каждой подгруппе проблемы. Метод МАИ является многокритериальным методом анализа на основе процесса взвешивания альтернатив, в котором несколько соответствующих атрибутов представлены через их относительной важности — веса. В классическом МАИ, важность нескольких атрибутов получается из процесса попарного сравнения, в котором значимость атрибутов или категорий нематериальных активов сопоставляются попарно.
Тем не менее, чистая модель МАИ имеет некоторые недостатки. В работе [20] Yang & Chen указали на то, что:
1) метод МАИ в основном используется в приложениях принятия решений на основе четкой информации;
2) МАИ создает и имеет дело с очень несбалансированной шкалой оценки;
3) метод МАИ не учитывает неопределенность, связанную с отображением человеческого суждения на естественном языке;
4) рейтинг метода МАИ весьма неточен;
5) большое влияние на результаты МАИ оказывают субъективные суждения, восприятия, оценки и отбор предпочтений лиц, принимающих решения (ЛПР).
Часто бывает трудно назначить точную оценку величин «эффективности» для рассматриваемых атрибутов альтернатив. Для преодоления этих проблем, некоторыми исследователями предложено интегрировать нечеткую теорию с методом анализа иерархий [21] (Buckley, 1985).
Достоинство использования нечеткого подхода состоит в назначении относительного значения атрибутов с использованием нечетких чисел, вместо точных. Нечеткое МАИ строится на основе нечеткой интервальной арифметики с треугольными (трапециевидными) нечеткими числами и доверительным интервалом среднего значения весовых коэффициентов для оценочных элементов.
Пусть имеется множество из m альтернатив 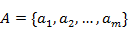 и имеется n критериев: и имеется n критериев: 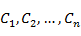 . Тогда для критерия . Тогда для критерия 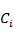 может быть рассмотрено нечеткое множество: может быть рассмотрено нечеткое множество:
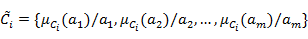 , ,
где 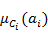 – оценка альтернативы – оценка альтернативы 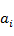 по критерию по критерию 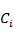 характеризует степень соответствия альтернативы понятию, определенному критерием характеризует степень соответствия альтернативы понятию, определенному критерием 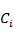 . Предположим, что также заданы (или рассчитаны, по одному из методов [22]) веса критериев . Предположим, что также заданы (или рассчитаны, по одному из методов [22]) веса критериев 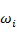 . .
Правило для выбора наилучшей альтернативы для многокритериальных задач не является формализованным, особенно в случае противоречивости альтернатив по различным критериям. Обычная практика – принятие решений ЛПР на основе результатов, полученных с использованием различных методов:
– свертки критериев: аддитивная (с весом); мультипликативная и др.;
– методов многомерного ранжирования: близость к «идеальной точке»; условного центра масс и др.;
– последовательных уступок;
– методы Парето.
Каждый из методов требует адаптации к условиям нечеткого задания атрибутов.
Если лучшей считается альтернатива, удовлетворяющая и критерию C1 и C2 и… и Cn, то правило в виде свертки критериев можно представить в виде пересечения соответствующих нечетких множеств:
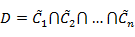
Метод «идеальной точки» (Technique for Order Performance by Similarity to Ideal Solution — TOPSIS) [23, 24] (Hwang & Yoon, 1981; Wang & Chang, 2007) основан на концепции, что выбранная альтернатива должна иметь кратчайшее расстояние от положительного идеального решения (то есть достижение минимальных пробелов в каждого критерия) и наибольшее расстояние от отрицательного идеального решения (то есть, достигая максимальных уровней в каждом из критерия). TOPSIS определяет индекс, определяемый сходство с положительно идеальным решением и удаленность от отрицательного идеального решения. Затем метод выбирает альтернативу с максимальным сходством с положительно идеальным решением.
В случае МАИ, оценка весов показателей в условиях нечетких входных данных проводится на основе построения и анализа нечетких матриц парных сравнений [12]. Нечеткая МПС представляет обобщение четкой МПС путем замены дискретных элементов матрицы на нечеткие числа с триангулярными функциями принадлежности. Для задания триангулярной функции принадлежности достаточно трех чисел (l, m, u). Поэтому, НМПС представляет собой прямоугольную матрицу размерности 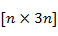 : :
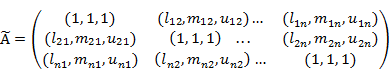
Обратно-симметричные элементы матрицы вычисляются по формулам:
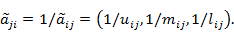
При построении НМПС используют, либо эмпирические шкалы, либо элементы вычисляют через параметрическое задание степени нечеткости. Эмпирические шкалы строятся на основе экспертной обработки степени относительной важности одного показателя над другим в нечеткой трактовке, т.е. с использованием триангулярной функции принадлежности. Пример такой шкалы приведен в таблице 1 [12].
Таблица 1 – Нечеткая шкала относительной важности показателей
|
Высказывание
|
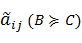
|
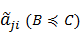
|
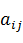
шкала Саати [7]
|
|
если отсутствует преимущество элемента
B над элементом C
|
(1, 1, 1)
|
(1, 1, 1)
|
1
|
|
если имеется слабое преимущество
|
(1, 3/2, 2)
|
(1/2, 2/3, 1)
|
3
|
|
если имеется существенное преимущество
|
(3/2, 2, 5/2)
|
(2/5, 1/2, 2/3)
|
5
|
|
если имеется явное преимущество
|
(2, 5/2, 3)
|
(1/3, 2/5, 1/2)
|
7
|
|
если имеется абсолютное преимущество
|
(5/2, 3, 7/2)
|
(2/7, 1/3, 2/5)
|
9
|
При параметрическом задании степени нечеткости 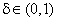 значения рангов для нечеткой матрицы рассчитывают по формуле: значения рангов для нечеткой матрицы рассчитывают по формуле:
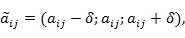
где 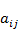 – средние четкие ранги приоритетов. – средние четкие ранги приоритетов.
Последовательность вычисления весов показателей следующая [13]:
1) рассчитывают суммы нечетких чисел по строкам матрицы 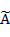 : :
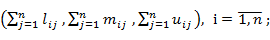
2) находят нормализованные построчные суммы:
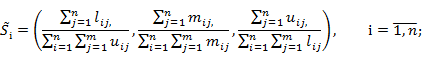
3) рассчитывают степень возможности того, что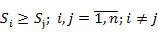 по уравнению: по уравнению:
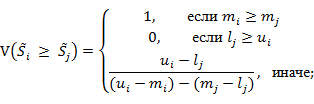
4) рассчитывают степень возможности того, что 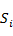 предпочтительнее всех остальных нечетких чисел: предпочтительнее всех остальных нечетких чисел:
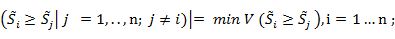
5) вектор приоритетов определяется по формуле:
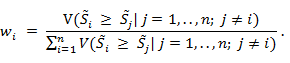
2.2 Метод нечеткого логического вывода
В случае невозможности четкой градации приоритета экспертом, альтернативой МАИ является метод нечеткого логического вывода (НЛВ), позволяющий экспертам оперировать лингвистическими переменными, такими как, «Низкий», «Средний», «Высокий». Формализация модели нечеткого логического вывода (НЛВ) следующий [15-19]:
1)субъективная оценка степени принадлежности элемента x к множеству A задается функцией принадлежности входных факторов в общем виде как:
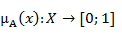
2) задают нечеткие правила, которые устанавливает взаимосвязь между заданными входами 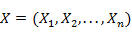 и выходом и выходом 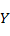 в виде: в виде:
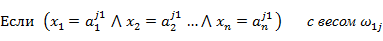
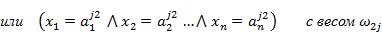
…
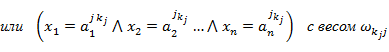
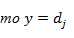 , ,
где 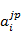 – нечеткий терм, которым оценивается лингвистическая входная переменная Xi в строке с номером jp (p= 1,…,kj); kj– количество строк-конъюнкций, в которых выход – лингвистическая выходная переменная Y оценивается термом dj ; m– количество термов, используемых для выходной лингвистической переменной Y. – нечеткий терм, которым оценивается лингвистическая входная переменная Xi в строке с номером jp (p= 1,…,kj); kj– количество строк-конъюнкций, в которых выход – лингвистическая выходная переменная Y оценивается термом dj ; m– количество термов, используемых для выходной лингвистической переменной Y.
3) степень принадлежности рассчитывается по формулам:
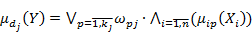 , ,
где 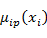 и и 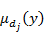 – функции принадлежности входа Xi и выхода Y нечеткому терму. – функции принадлежности входа Xi и выхода Y нечеткому терму.
Привлекательность оценивания показателей на основе НЛВ состоит в том, что метод позволяет небольшим количеством нечетких правил адекватно описать многомерные зависимости «вход-выход». Однако, результаты нечетких выводов полностью определяются корректностью построения функций принадлежности входных факторов и выходного параметра, построением адекватной базы знаний правил нечеткого логического вывода и выбором процедуры дефаззификации результирующего показателя.
3. Пример реализации нечетко-логических инструментов для принятия решений по оценке надежности нефтехимического оборудования
3.1 Постановка задачи
По разным оценкам [25, 26], более 80% оборудования, находящегося в эксплуатации на нефтегазохимических предприятиях России выработало свой ресурс. В условиях общего экономического спада, прогнозные сроки обновления оборудования составляют 20-30 лет. Это вынуждает предприятия искать пути продления сроков службы и одновременного увеличения надежности эксплуатации в условиях взрыво-пожароопасной среды.
Один из путей продления сроков службы оборудования – проведение тотальной диагностики и последующей сертификации всего парка оборудования – является трудоемким и дорогостоящим мероприятием.
Сокращение расходов и оптимизация возможны при условии оперативного определения общего состояния надежности, прогнозировании надежности химико-технологических систем (ХТС), а также оценке «потенциально опасного участка» применительно конкретных производств и условий эксплуатации нефтезаводского оборудования, учитывающего особенности его конструкции, эксплуатации, результаты диагностических работ, ремонта и т.д. В ситуации, когда ряд единичных показателей надежности объекта превышают свои нормативные значения, а другие удовлетворяют требованиям стандартов, возникают вопрос о возможном продлении срока службы. На основании полученных оценок возможна разработка плана мероприятий повышающих надежность ХТС, выработка рекомендаций при проведении диагностических работ, планирование надежности и прогнозирования остаточного ресурса промышленного оборудования на основе существующих знаний и опыта эксплуатации.
Таким образом, задача состоит в разработке неформализованных процедур оценки общего технического состояния надежности всей системы в целом и отдельных ее элементов, которые выполняются на основании экспертных заключений специалистов. Полученные на данном этапе выводы, являются основой формирования программы работ диагностирования показателей надежности и планирования работ по замене оборудования.
3.2 Построение иерархической структуры показателей надежности
Этап общей экспертной оценки технического состояния ХТС начинается с выбора единичных показателей, для которых возможна либо количественная оценка, либо возможна экспертная оценка, например в балльной шкале или в вербальной форме.
Показатели надежности регламентируются в ГОСТ, отраслевых стандартах или руководящих документах [27, 28]. Там же приводятся зависимости для расчета этих показателей, представляющие собой характеристики вероятностных или статистических математических моделей создаваемых объектов. На рисунке 1 представлена иерархическая структура единичных показателей надежности согласно ГОСТ 27.002-89.
Полнота исходной информации зависит от того, использует ли предприятие автоматизированные комплексные системы управления и обеспечения надежности промышленного производства. По ряду показателей актуальная информация может отсутствовать. Кроме этого, часть показателей в иерархии (рис. 2) носит вероятностный характер, а показатели, полученные в результате экспертного оценивания, обладают свойством нечеткости. Нечеткость высказываний экспертов определена субъективным восприятием и оценкой значимости и важности тех или иных показателей [7-9]. Например, для одного эксперта понятие «Высокая вероятность отказа» может характеризоваться числом 7, а для другого – числом 9 в десяти-балльной шкале. Будем считать, что, если хотя бы один показатель оценивается, а не измеряется, то сводное значение показателя в вершине иерархии носит оценочный, а не точный характер, независимо от числа четких показателей. То же самое верно для промежуточных показателей.

Рисунок 2 – Иерархическая структура единичных показателей надежности
3.3 Оценка надежности нефтегазохимического оборудования
Для оценки каждого показателя из сформированной древовидной системы показателей (рис.2) необходимо задать лингвистическую и универсальную шкалу оценки, разработать метод определения веса каждого показателя (той степени, с которой он влияет на более высокий по иерархии показатель), сформировать базы правил для НЛВ показателя, находящегося в вершине иерархии, и определить свертку для операции НЛВ по базам правил. В общем случае к разным группам показателей из иерархии могут применяться разные методы измерения (МАИ или НЛВ). При этом получатся результаты оценок и сводные значения по каждому из методов измерения. Далее в модели анализа агрегируются значения, полученные разными методами, и выводится результирующий индикатор. После процесса интерпретации получается количественное значение интегрированного показателя, являющееся выходным результатом процесса измерения
Реализация нечетко-логических процедур по управлению комплексом показателей надежности выполнена по результатам экспертного оценивания надежности четырех отдельных производственных объектов единой сложной организационно-технической системы нефтегазохимического производства по пяти показателям надежности.
Методика НМАИ
После рассмотрения соответствующей литературы [29, 30], мы установили критерии построения систем иерархии оценки. В МАИ единичные показатели надежности будут выступать в качестве критериев. В качестве единичных показателей надежности рассматриваются следующие: два показателя из группы «безотказность» – вероятность безотказной работы (Pt), средняя наработка на отказ (То); два показателя из группы «долговечность» – прогноз ресурса оборудования (Tр), не выработавшего нормативный срок службы, остаточный ресурс оборудования, работающего сверх нормативного срока (Трс); и один показатель из группы «работоспособность» – вероятность восстановления в заданное время (Pв). На этапе предварительной оценки общей надежности оборудования предполагается, что количественные оценки указанных показателей неизвестны и могут быть оценены экспертами либо в балльной шкале, либо с использованием лингвистических термов. Задача состоит в определении количественной оценки надежности рассматриваемых четырех объектов по пяти критериям для выявления приоритетов мероприятий по обеспечению надежности, так как стратегия должна быть сбалансирована в соответствии со степенью риска.
Первый этап МАИ состоит в определении весов критериев, который выполнен с помощью построения четкой МПС, поскольку у экспертов имеется ясное понимание приоритетов критериев в соответствии с задачей предприятия в обеспечении надежности функционирования ХТС. Ранги приоритетов матрицы парных сравнений расставлены в соответствие со шкалой Саати [7]. Матрица парных сравнений критериев одного из экспертов и результаты оценки весов по методу МАИ представлены в таблице 2.
Таблица 2 – Пример четкой МПС приоритетов критериев надежности для первого эксперта
| |
Критерии
|
Критерий согласованности МПС:
|
| |
Pt
|
То
|
Тр
|
Трс
|
Pв
|
Веса
|
|
Pt
|
1
|
2
|
3
|
3
|
4
|
0,397
|
ИС= 0,032 < 0,1
ОС= 0,029 < 0,1
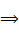 оценки приоритетов в МПС согласованы оценки приоритетов в МПС согласованы
|
|
То
|
0,5
|
1
|
2
|
2
|
3
|
0,242
|
|
Тр
|
1/2
|
1/3
|
1
|
1
|
2
|
0,136
|
|
Трс
|
1/3
|
1/2
|
1
|
1
|
2
|
0,147
|
|
Pв
|
1/4
|
1/3
|
1/2
|
1/2
|
1
|
0,078
|
Для каждого из исследуемых производственных объектов проведем экспертную оценку весов надежности по каждому из пяти критериев на основании данных экспертного оценивания пяти экспертов. В таблице 3 представлен пример нечеткой МПС для оценки весов надежности для четырех объектов по первому критерию на основании оценок первого эксперта.
Таблица 3 – Пример нечеткой МПС для оценки весов надежности четырех объектов по первому критерию (Pt), δ=0,5
| |
Объект 1
|
Объект 2
|
Объект 3
|
Объект 4
|
|
Объект 1
|
1
|
1
|
1
|
1,25
|
2
|
2,75
|
2,25
|
3
|
3,75
|
2,25
|
3
|
3,75
|
|
Объект 2
|
0,36
|
0,5
|
0,8
|
1
|
1
|
1
|
1,25
|
2
|
2,75
|
1,25
|
2
|
2,75
|
|
Объект 3
|
0,27
|
0,33
|
0,44
|
0,36
|
0,5
|
0,8
|
1
|
1
|
1
|
1,25
|
2
|
2,75
|
|
Объект 4
|
0,27
|
0,33
|
0,44
|
0,36
|
0,5
|
0,8
|
0,364
|
0,5
|
0,8
|
1
|
1
|
1
|
Аналогичным образом составляются нечеткие матрицы парных сравнений для всех объектов по всем выбранным критериям. Обработки НМПС проведены в соответствии с описанной выше методикой с использованием программного комплекса, реализованного в среде MatLab и MS Excel. Результаты приведены в таблице 4.
Таблица 4 – Результаты оценки весов надежности четырех объектов по пяти критериям с использованием нечеткой МПС, δ=0,75
|
|
Веса общей надежности относительно критерия
|
Вес надежности объекта
|
|
Критерии
|
Pt
|
То
|
Тр
|
Трс
|
Pв
|
|
Средний вес 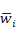
|
0,303
|
0,228
|
0,184
|
0,165
|
0,120
|
|
Объект 1
|
0,46
|
0,34
|
0,15
|
0,25
|
0,04
|
0,29
|
|
Объект 2
|
0,26
|
0,34
|
0,27
|
0,27
|
0,20
|
0,27
|
|
Объект 3
|
0,20
|
0,17
|
0,55
|
0,42
|
0,33
|
0,31
|
|
Объект 4
|
0,08
|
0,15
|
0,03
|
0,06
|
0,43
|
0,13
|
При изменении степени нечеткости, веса показателей надежности объектов выравниваются. Действительно, степень нечеткости сглаживает приоритеты, определенные в матрице парных сравнений. Такую закономерность иллюстрирует рисунок 3.
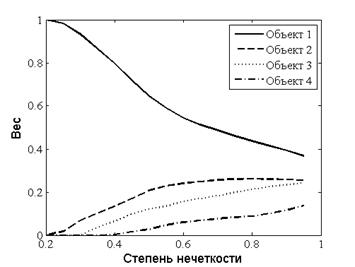
Рисунок 3 – Изменение весов надежности производственных объектов в зависимости от степени нечеткости относительно первого критерия Pt
Аналогичные результаты имеют место и для остальных рассматриваемых критериев. Для значений нечеткости в интервале δ=0,2—0,4 метод нечетких МПС имеет слабую чувствительность к приоритетам экспертов и устанавливает вес одного из объектов, близкий к единице. В интервале значений δ=0,75—0,95 приоритеты НМПС сглаживаются и веса всех объектов выравниваются. Значимо различимые результаты весов имеют место для значений параметра нечеткости δ=0,5—0,75.
Методика НЛВ
В модели НЛВ в качестве исходных данных выступают нечеткие оценки единичных показателей надежности производственных объектов, выраженные в лингвистической форме. Для оценки показателя надежности каждого из четырех объектов ХТС на стадии предварительного отбора объектов для последующего комплексного исследования надежности объекта необходимо задать лингвистическую и универсальную шкалу оценки.
Предполагается, что входные факторы нечеткие и определяются трехуровневыми нечеткими термами «НИЗКОЕ», «СРЕДНЕЕ» и «ВЫСОКОЕ» значение, с обозначением L, M и H соответственно. Функцию принадлежности нечетким термам определим в виде триангулярной функции, «треугольные» числа (l, m, u) которых определены эмпирическим способом.
Адекватность модели НЛВ полностью зависит от правильной формализации входных данных и адекватного построения правил логического вывода.
База данных логистических правил оценивания общего показателя надежности производственного объекта на основании значений единичных показателей надежности также построена на основании экспертного оценивания. В таблице 5 представлен фрагмент базы данных лингвистических правил оценивания общего показателя надежности на трехуровневом классификаторе по пяти входным факторам. Общее число правил полного факторного эксперимента равно 35=243.
Таблица 5 – Фрагмент логистических правил оценивания общего показателя надежности на основе лингвистические значений единичных показателей
|
Сценарий
|
|
Лингвистические значения частных показателей надежности объекта (&)
|
|
Общий показатель надежности
|
|
Pt
|
То
|
Тр
|
Трс
|
Pв
|
|
Терм
|
|
1
|
If
|
L
|
L
|
L
|
L
|
L
|
Then
|
L
|
|
2
|
If
|
L
|
L
|
L
|
L
|
M
|
Then
|
L
|
|
3
|
If
|
L
|
L
|
L
|
L
|
H
|
Then
|
L
|
|
…
|
|
|
|
|
|
|
|
|
|
12
|
If
|
L
|
L
|
M
|
L
|
H
|
Then
|
M
|
|
…
|
|
|
|
|
|
|
|
|
|
243
|
If
|
H
|
H
|
H
|
H
|
H
|
Then
|
H
|
Количественную оценку веса общего показателя надежности каждого объекта Y проводят с использованием стандартной процедуры дефаззификации лингвистической переменной 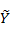 по алгоритму Мамдани. Для процедуры дефаззификации использовали функцию принадлежности триангулярного вида на пятиуровневом классификаторе с лингвистическими термами «низкое», «невысокое», «среднее», «выше среднего» и «высокое» с обозначением L, ML, M, MH и H соответственно. по алгоритму Мамдани. Для процедуры дефаззификации использовали функцию принадлежности триангулярного вида на пятиуровневом классификаторе с лингвистическими термами «низкое», «невысокое», «среднее», «выше среднего» и «высокое» с обозначением L, ML, M, MH и H соответственно.
Реализация модели НЛВ для оценки показателей надежности четырех производственных объектов выполнена в модуле Fuzzy Logic Toolbox системы MatLab.
Исходные значения лингвистических термов единичных показателей надежности для каждого из объектов задавались пятью экспертами. В результате проведения расчетов по модели НЛВ получены следующие средние значения весов общей надежности каждого из четырех объектов, представленные в таблице 6.
Таблица 6 – Результаты оценки весов надежности четырех объектов по пяти единичным показателям с использованием НЛВ
|
Производст-венные объекты
|
Значения единичных показателей надежности
|
Надежность объекта,
отн. ед.
|
Нормиро-ванное
значение
|
|
Pt
|
То, лет
|
Тр, лет
|
Трс, лет
|
Pв
|
|
Объект 1
|
0,8
|
2,2
|
5,4
|
2,8
|
0,7
|
0,574
|
0,28
|
|
Объект 2
|
0,75
|
2
|
5,0
|
3,0
|
0,8
|
0,500
|
0,24
|
|
Объект 3
|
0,9
|
2,5
|
6
|
3
|
0,75
|
0,625
|
0,30
|
|
Объект 4
|
0,7
|
1
|
3
|
2
|
0,9
|
0,375
|
0,18
|
4 Обсуждение результатов
На основании полученных весов по методике НМАИ можно сделать вывод, что четвертый производственный объект единой сложной технической системы нефтегазохимического производства является наиболее проблемным по общей надежности. Однако, он же является наиболее восстанавливаемым.
Результаты, полученные с применением «нечеткой» методики МПС сопоставимы с результатами, полученными на основе методики НЛВ. И в этом случае четвертый объект имеет наименьший результирующий ранг надежности.
Таким образом, нечеткая методология позволяет устранить проблему неопределенности и нечеткости, являющейся неотъемлемой частью исходной информации о сложной многофакторной системе, со сложными взаимодействиями составляющий систему элементов, в силу невозможности четкой градации приоритета экспертом.
МАИ выгодно применять, когда сложно формализовать входные данные четким или нечетким образом, поскольку в МАИ используется относительная шкала парных сравнений. Однако, при построении интеллектуальных систем поддержки принятия решений МАИ менее предпочтительно, так как эксперту приходится постоянно заполнять матрицы парных сравнений. Еще один недостаток МАИ состоит в слабой различимости общих рангов предпочтений альтернатив при их большом числе, уже когда их больше 5-7.
Результаты метода НЛВ имеют сильную зависимость от правильной формализации функций принадлежности входных данных, а также от корректного построения нечетких баз правил. Для устранения этого недостатка, при проектировании экспертной системы необходимо реализовать систему обратной связи, позволяющую по результатам эксплуатации корректировать как фаззификатор, так и базу правил логического вывода. В этом случае экспертная система может именоваться как интеллектуальная система поддержки принятия решений.
Представленный пример системы поддержки принятия решений по управлению комплексом показателей надежности нефтегазохимического оборудования решает задачу предварительной оценки общего состояния надежности оборудования. Такие подсистемы поддержки принятия решений являются неформализованной частью комплексных систем управления и обеспечения надежности промышленного производства.
References
1. Eshbi R. Vvedenie v kibernetiku. – M.: KomKniga, 2005. – 432 s.
2. Mesarovich M., Mako D., Takakhara M. Teoriya ierarkhicheskikh mnogourovnevykh sistem. – M.: Mir, 1973. – 344 s.
3. Figueira J., Greco S. and Ehrgott M. (eds.) Multiple Criteria Decision Analysis: State of the Art Surveys. – New York: Springer Science & Business Media, 2005. – 1045 pp.
4. Wallenius J., Dyer J. S., Fishburn P. C., Steuer R. E., Zionts S. and Deb K. Multiple criteria decision making, multiattribute utility theory: Recent accomplishments and what lies ahead // Management Science. – 2008. – V. 54(7). – P. 1336-1349.
5. Roy B. Multicriteria Methodology for Decision Aiding. – Boston: Springer, 1996.– 316 pp.
6. Saaty T. L. The Analytic Hierarchy Process. – New York: McGraw-Hill, 1980. – 296 pp.
7. Saati T. Prinyatie reshenii. Metod analiza ierarkhii. – M.: Radio i svyaz', 1993. – 278 s.
8. Zade L. Ponyatie lingvisticheskoi peremennoi i ee primenenie k prinyatiyu priblizhennykh reshenii. – M.: Mir, 1976. – 167 s.
9. Kofman A. Vvedenie v teoriyu nechetkikh mnozhestv. – M.: Radio i svyaz', 1982. – 432 s.
10. Kaufman A., Gupta M. M. Fuzzy Mathematical Models in Engineering and Management Science. – North-Holland, Amsterdam. – 1988. – 338 pp.
11. Chang D.Y. Applications of the extent analysis method on fuzzy AHP // European Journal of Operational Research. – 1996. – V. 95. – № 3. – P. 649-655.
12. Chang D.Y. Extent analysis and synthetic decision, optimization techniques and applications, Vol. 1, Singapore: World Scientific, 1992. – 352 pp.
13. Zhu K. J., Jing D. Y. A discussion on extent analysis method and applications of fuzzy AHP // European Journal of Operational Research. – 1999. – V. 116. – P. 450-456.
14. Degtyarev A.N., Mukhametzyanov I.Z., Rozhkova N.V. Metodologiya postroeniya ierarkhicheskoi sistemy pokazatelei razvitiya v sfere turisticheskogo biznesa na osnove nechetko-logicheskikh protsedur prinyatiya reshenii // Teoreticheskaya i prikladnaya ekonomika. – 2016.-№ 1.-S.45-57. DOI: 10.7256/2409-8647.2016.1.19102. URL: http://e-notabene.ru/etc/article_19102.html
15. Mamdani E. H. and Assilian S. An experiment in linguistic synthesis with a fuzzy logic controller // Int. J. Man-Mach. Stud. – 1975. – V. 7. – P. 1-13,
16. Takagi T. and Sugeno M. Fuzzy identification of systems and its applications to modeling and control // IEEE Tran. Syst., Man, Cybern. –1985. – V. SMC 15. – P. 116-132.
17. Zimmermann H.J. Fuzzy Set Theory and Its Application; Kluwer Academic Publishers: London, UK, 1991. – 514 pp.
18. Mukhametzyanov I.Z., Meshalkin V.P. Imitatsionnaya mnogoagentnaya nechetko-logicheskaya model' prinyatiya marketingovykh reshenii promyshlennogo predpriyatiya v usloviyakh neopredelennosti // Prikladnaya informatika. – 2014. – №3 (51). – S. 100-109.
19. Mukhametzyanov I.Z., Meshalkin V.P. Nechetko-logicheskaya protsedura prognozirovaniya razvitiya neftepererabatyvayushchikh predpriyatii v usloviyakh neopredelennosti // Neftegazovoe delo. – 2014. – №4. – S. 126-133.
20. Yang, C.-C., & Chen, B.-S. (). Key quality performance evaluation using fuzzy AHP // Journal of the Chinese Institute of Industrial Engineers. – 2004. – V. 21(6) . – P. 543-550.
21. Buckley J.J. Fuzzy Hierarchical Analysis // Fuzzy Sets and Systems. – 1985. – V. 17. – P. 233-247.
22. Korobov V.B. Sravnitel'nyi analiz metodov opredeleniya vesovykh koeffitsientov «vliyayushchikh faktorov» // Sotsiologiya: 4M. – 2005. – №20. – S.54-73.
23. Hwang C.-L., & Yoon K. Multiple attribute decision making: methods and applications. In Lecture notes in economics and mathematical systems. Now York: Springer, 1981. – 259 pp.
24. Wang T.-C., Chang T.-H. Application of TOPSIS in evaluating initial training aircraft under a fuzzy environment // Expert Systems with Applications. – 2007. – V. 33. – P. 870-880.
25. Rossiiskii statisticheskii ezhegodnik. 2015: Stat.sb./Rosstat. – R76. M.: 2015. – 728 s.
26. Godovoi otchet o deyatel'nosti Federal'noi sluzhby po ekologicheskomu, tekhnologicheskomu i atomnomu nadzoru v 2014 godu // Federal'naya sluzhba po ekologicheskomu, tekhnologicheskomu i atomnomu nadzoru. M.: 2014. – 442 s.
27. GOST 27.002-89. Nadezhnost' v tekhnike. Osnovnye ponyatiya. Terminy i opredeleniya. M.: MNTK "Nadezhnost' mashin". 1988. – 58 s.
28. GOST 27.301-95. Nadezhnost' v tekhnike. Raschet nadezhnosti. Osnovnye polozheniya.
29. Kafarov V.V., Meshalkin V.P. Nadezhnost' oborudovaniya i tekhnologicheskikh skhem khimicheskikh i neftekhimicheskikh proizvodstv. – M.: Khimiya, 1979. – 167 s.
30. Meshalkin V.P. Ekspertnye sistemy v khimicheskoi tekhnologii. – M.: Khimiya, 1995. – 367 s.
|
















 This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

