Solving Topical Issues of Oil Companies Using the Game Theory Method

Введение

Статья посвящена исследованию ряда проблем предприятий нефтегазовой отрасли в терминах теории игр. У текста двойная цель: показать набор перспектив, с которых изучаются нефтегазовые компании, с одной стороны, с другой – показать, как в данный набор вписывается методология теории игр и перспектива симуляционного моделирования. Для этого я выделю три, на мой взгляд, ключевые проблемы для компании нефтегазовой отрасли, и предложу способ решения с помощью методов теории игр. Перед данной статьей не ставится цель предложить комплексный и всеобъемлющий подход для решения каждой из проблем, но показать, какие перспективы открывает теория игр для решения каждой из них.

Применение методов теории игр в информационной безопасности

Развитие информационных технологий позволило автоматизировать способы добычи и переработки нефти и газа. Обеспечение защищенности информационных процессов в автоматизированных системах управления технологическими процессами на предприятиях нефтедобывающей отрасли – ключевой аспект бизнес стратегии, так реализация угроз безопасности может привести к значительному материальному и экологическому ущербу.

Использование методов теории игр позволит наиболее оптимально моделировать действия обеих сторон. Так как конфликт, лежащий в основе защиты, между потенциальным нарушителем и стороной, обеспечивающей безопасность информации, носит антагонистический характер, т.е. цели сторон заведомо противоположны. Теория игр позволяет выработать стратегию рационального поведения для достижения максимального выигрыша или максимальной вероятности выигрыша ^[1].

Различная ценность информационных ресурсов предъявляет соответствующие требования к системе защиты. Возникающие при этом две ситуации, предполагают решение принципиально различных задач.

Первая ситуация предполагает, что защищаемая информация является сведениями, составляющими государственную тайну и возможность определения степени ущерба от её потери отсутствует. Основным требованием к системе защиты, в данном случае, является обеспечение требуемого высокого уровня защищенности, а задача оптимизации состоит в том, чтобы максимально сократить затраты на обеспечение уровня защищенности.

Вторая ситуация предполагает наличие конфиденциальной информации или информации, составляющей коммерческую тайну. В данном случае, следствием реализации угроз безопасности будет экономический ущерб, который можно оценить эмпирически. Тогда стратегия системы защиты информации должна быть направлена на то, чтобы затраты потенциального нарушителя на преодоление системы защиты были соизмеримы со стоимостью самой системы защиты и предполагаемого экономического ущерба. Задача оптимизации заключается в том, чтобы размер затрат на систему защиты не превышал 10 процентов стоимости самой информации, а также в обеспечении максимального уровня защищенности.

Разумно предположить, что при моделировании угроз безопасности были выбраны оптимальные средства защиты, организационные и правовые меры, перекрывающие все актуальные угрозы безопасности. А также проведено обучение персонала и перекрыты все технические каналы утечки. Тогда, при известном конечном числе угроз, можно определить реакцию на них системы защиты. Большинство существующих угроз безопасности информации отражено в Банке угроз ФСТЭК.

Ключевое преимущество теории игр в том, что она позволяет определить наиболее рациональную стратегию поведения как потенциального нарушителя, так и стороны, обеспечивающей безопасность. Анализ стратегии первого позволяет выявить слабые места в системе защиты и устранить их. Данная модель относится к классу игр с неполной информацией.

Определим следующие характеристики: количество объектов защиты – l; количество средств защиты – m; количество угроз безопасности – n; коэффициенты опасности угроз для каждого k объекта - 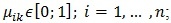коэффициент эффективности использования механизма защиты j от i-ой угрозы к объектам защиты – k=1, … ,l; 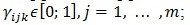затраты на реализацию угрозы - a_ik; стоимость средств защиты информации - b_jk; ценность объекта -C_k.

Тогда игровую матрицу для описания вероятных воздействий на объект защиты при различных комбинациях средств и мер защиты можно построить на основе целевой формулы:

,

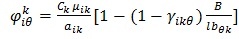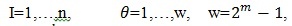
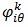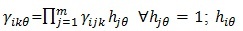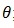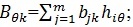где – элемент матрицы для объекта k; - коэффициент использования механизма защиты j в варианте системы защиты ; B – суммарная стоимость системы защиты.

Построенная с помощью с данной модели и индивидуальных для каждого объекта защиты эмпирических данных платежная матрица позволит провести комплексный анализ системы информационной безопасности, выявить актуальные модели нарушителя, определить объекты системы, являющиеся наиболее приоритетными целями для потенциального нарушителя, и выбрать оптимальную стратегию защиты.

Учитывая специфику нефтегазовой отрасли, удаленность многих объектов от АСУ ТП, а также величину ущерба, не только экономического и репутационного, но и экологического, связанного с реализацией угроз безопасности важно проводить подобное моделирование, учитывающие все факторы, начиная с мотивации и оснащенности нарушителя, и заканчивая степенью лояльности персонала в вопросах информационной безопасности в общем, и реализацией приемов социальной инженерии в частности.

Применение теории игр при формировании конкурентной стратегии на рынке нефтепродуктов

Для компании, которая ведет добычу нефти и газа во многих уголках земли, как на суше, так и на шельфе, доказанные запасы которой составляют несколько миллиардов тонн жидких углеводородов и более триллиона кубических метров природного газа, важно не только сохранять лидирующее положение на рынке. Так же важно своевременно реагировать на изменяющиеся факторы окружающей среды, которые могут быть обусловлены как действиями конкурентов, так и природными явлениями. Инциденты при добыче и транспортировке углеводородов могут повлечь за собой значительные экономические издержки и приводить к колоссальному экологическому ущербу. В частности, после аварии 2010 года в мексиканском заливе, когда компания BP испытывала значительные экономические трудности, её главные конкуренты, в том числе французская Total, российская Роснефть, а также Exxon, Shell и Conoco, открыто заявляли, что в случае продажи британской компании по частям, вопрос частичного поглощения будет рассмотрен.

В формировании конкурентной стратегии ключевую роль должна играть экономико-математическая модель формирования конкурентной стратегии. Инструментарий теории игр позволяет наиболее достоверно моделировать конфликты между игроками в условиях неопределенности при принятии решений ^[2].

Модель должна быть основана на следующих предположениях. Имеются два игрока. Первый игрок – условная нефтегазовая компания с ежегодной выручкой более 100 миллиардов долларов. Необходимо учитывать индивидуальные показатели воздействия на первого игрока со стороны окружающей среды, учитывать вероятность природных катаклизмов и сопряженную с ней вероятность техногенной аварии и вытекающий из этого экологический ущерб, пороговые значения, переменные управления. А также настроение финансового рынка. Второй игрок – представлен как одно целое из группы, включающей восемь наиболее крупных нефтегазовых компаний: BP, Sinopec, Royal Dutch Shell, ExxonMobil, Chevron, PetroChina, Total, Philips 66. Конкуренты были выбраны по результатам кластерного анализа, проведенного на основании ключевых показателей: выручка, чистая прибыль, активы, рыночная стоимость, число сотрудников.

В каждый момент времени действия игроков приводят к перераспределению активов. Рассматриваемая игра не является игрой с постоянной суммой, т.к. потенциальные объемы активов, выручки и чистой прибыли могут несколько превышать сумму по всем игрокам, также игра не является кооперативной.

Конкурентная стратегия игроков заключается в управлении тремя переменными: активы, чистая прибыль и риски со стороны окружающей среды. Взаимодействие данных факторов будут представлять возможные игровые ситуации.

Цель игроков предполагает максимизацию чистой прибыли. В то же время, конкурентная стратегия должна учитывать перспективы, учитывая современные рыночные условия горизонт планирования в 5 лет является достаточным.

Для построения модели игры можно использовать данные об основных показателях нефтедобывающей деятельности: общий объем добычи углеводородов, коэффициент восполнения доказанных запасов, общая производительность перерабатывающих предприятий, общий объем нефтехимического производства, прибыль (убыток) за вычетом изменений оценки стоимости запасов продукции, налоговые платежи, дивиденды акционерам.

В качестве эмпирических показателей воздействия на окружающую среду можно использовать данные об количестве случаев разлива нефти на суше и на воде, объеме неудалённой нефти, прямых выбросах двуокиси углерода и метана, частоте ураганов в зонах добычи на шельфе, сейсмологической активности в местах пролегания нефтепроводов.

Использование следующих классических критериев позволит произвести оптимальный выбор стратегии игры с учетом фактора окружающей среды:

1. Максимальный критерий, является критерием крайнего оптимизма и ориентирует компанию на наиболее благоприятные условия окружающей среды. Данным критерием пользуются в случае, если перед игроком стоит выбор между получением наибольшего выигрыша либо риска стать банкротом ^{[10, 11]};
2. Критерий крайнего пессимизма Вальда ориентирует игрока на наиболее неблагоприятные для него условия окружающей среды, следовательно, на осторожное поведение при выборе стратегии. Данный критерий применяется в тех случаях, когда игрок стремится не столько выиграть, сколько не проиграть, в нашем случае не получить экономических издержек, связанных с экологическим ущербом ^[12].

Тогда целевую функцию выигрыша можно представить следующим образом:

,

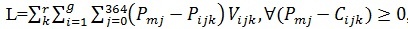где L – годовая чистая прибыль;

P_mj – выручка на j-ый квартал;

P_ijk, V_ijk – значения стоимости добычи, расходов на обслуживание рисков, иные издержки и рыночного объема актива i игрока k на соответствующие j-ые сутки;

g – количество единиц актива игрока k;

r – количество компаний в составе игрока.

В качестве стратегии первого игрока будем принимать строки x_i (i=1,…,n), а в качестве стратегии второго игрока столбцы y_i (j=1,…,m). Тогда таблица матричной игры примет вид, изображенный на Таблице 1, где коэффициент a_ij отражает совокупность выбранных ранее трех переменных: активы, чистая прибыль, риски.

Таблица 1.

Отмети два подхода к решению биматричных игр:

1. Поиск оптимальных ситуаций по Парето, заключающейся в невозможности игроков совместными усилиями увеличить выигрыш одного игрока, не уменьшив при этом выигрыш другого.
2. Поиск равновесных ситуаций, который заключается в поиске условий, при которых игра находится в некотором равновесии, которое невыгодно нарушать ни одному их игроков в отдельности.

В биматричной игре всегда присутствует как минимум одна точка равновесия по Нэшу. При этом возможны следующие варианты ^{[3, 14-17]}:

а) два равновесия по Нэшу в чистых стратегиях;

б) три равновесия по Нэшу – два в чистых и одно в смешанных стратегиях;

в) единственное равновесие по Нэшу в чистых стратегиях;

г) единственное равновесие по Нэшу в смешанных стратегиях;

д) континуум равновесий по Нэшу в смешанных стратегиях.

Таким образом, построенная платежная матрица позволит более точно определить вероятности исходов после определенных управленческих решений. Более того, понимание наиболее оптимальной модели поведение конкурентов в определенных ситуациях, позволит принимать наиболее взвешенное решение, учитывающее не просто все ключевые факторы, но и потенциальное влияние данного управленческого решения на действия конкурентов. Для максимального приближения к реальности моделирования посредствам заполнения платежной матрицы для каждого игрока необходимо учитывать, что эффект шума, оказывающий значительное влияние на результаты в других областях, при моделировании действий нефтегазовой компании минимален, так как все решения являются результатом экономически оптимальных расчетов. А эффект памяти наоборот весьма гибок, и зависит от ряда условий, которые, по большей части, сложно моделировать.

Анализ переговорной силы в поставках углеводородов

Методология игр является полезным инструментом при анализе переговорной силы сторон в поставках углеводородного сырья.

Возможность данного анализа с применением теории игр продемонстрировали Ф. Хуберт и С. Иконникова, которые подробно проанализировали евроазиатскую сеть поставки российского газа в Европу ^[4]. Они использовали кооперативную теорию игр для анализа того, какое влияние оказывает архитектура системы трубопроводов на положение сил в цепочке поставок российского газа.

Данные, полученные во время исследования показали, что конкуренция между Белоруссией и Украиной не имеет большого стратегического значения по сравнению с российским проектом «Северный поток», который дает возможность для России через море получить прямой доступ к потребителю.

Интересно, что с целью количественной оценки стратегического значения различных инвестиционных вариантов по расширению сети, использовав вектор Шепли, исследователи установили, что такие проекты как Baltic и Bypass, не смотря на заявленные цели, имеют ограниченное стратегическое значение, а увеличение мощности уже существующей магистрали Yamal или South баланс сил практически не меняет.

Практическое значение данного исследования заключается еще и в проведенном сравнении различных концепций решений, показавшее, что в вопросе переговорной силы при поставках углеводородного сырья наиболее оптимальный результат можно получить используя концепцию вектора Шепли, а не ядра или нуклеолуса. Не смотря на присутствовавшие при написании статьи ограничения индекс силы, рассчитанный для составной игры, оказался устойчивым к изменениям в параметрах калибровки модели.

Заключение

Я попытался предложить несколько направлений для исследования применения методов теории игр для решения актуальных проблем нефтегазовых компаний. За гранью обзора остался большой объем проблем, применение методов теории игр в которых, могло бы привести к значительной оптимизации эффективности решения каждой из них. Мы увидели, что аппарат теории игр очень гибок, и позволяет описывать даже такие специфические задачи, как обеспечение информационной безопасности нефтегазовой компании и формирование конкурентной стратегии. Более того, сформированный математический аппарат, при наличии достаточного количества эмпирических данных и проведении системного анализа открывает большие перспективы для дальнейших исследований. Наконец, доведение до логического завершения указанного исследования позволит использовать его результаты в качестве источника моделей взаимодействия, то есть приносить реальный вклад в оптимизацию бизнес-процессов, который сложно оценить на данном этапе.