|
DOI: 10.7256/2306-4196.2016.4.19863
Received:
26-07-2016
Published:
26-08-2016
Abstract:
The article is devoted to the question whether it is possible to execute modeling and computer-aided evaluation of students' competency levels based on the analysis of their decisions. The emphasis is made on the method of constructing the structure of complicating of routine tasks and operational space of potential solutions. Based on the preset operational space, the authors of the article suggest to create expert agents which solutions will serve as the basis for further analysis of rationality and completeness of students' decisions. As a result of the students' decision anaylsis, the authors develop their competency map. The level of competency is defined by the difficulty of routine tasks soloved by students as part of the given knowledge module. The research involves modeling particular components of the decision making process and interaction methods when making a decision about the level of students' competency. The main conclusions of the research are the following. Firstly, the aforesaid model of the decision operational space, on the one hand, limits a possible set of applicable basic operations and enables formulation and logging of users' decisions by the testing system and, on the other hand, gives freedom to students in the process of constructing potential decisions. Secondly, the array of routine task complication constitutes a good basis for constructing the competency map of a student in a form of an overlay model, allows to model and evaluate the level of competency in accorance with the level of difficulty of tasks being solved, and enables to arrange for adaptive testing that takes into account individual features of students. Thirdly, the data structures introduced in the operational space of decision making can be adjusted in accordance with the incoming information in order to be adequate. The models reviewed create a good basis for implementing multiagent and neural network paradigms for programming intelligence systems of testing.
Keywords:
intelligence system of testing, competency levels, classifying learners, decision operational space, competency overlay model, assignments enclosuring structure, adaptive learning environment, case structure, multiagent environment, knowledge module
Введение Современная гегемония социального конструктивизма, компетентностного подхода в обучении нацеливают нас на изменение самой направленности обучения от процесса передачи знаний к процессу организации решения компетентностных задач в сотрудничестве. Обучающиеся теперь сами должны уметь добывать необходимые знания для решения поставленных задач, учиться решать эти задачи в сотрудничестве и с преподавателем, и с другими обучающимися.
Формулируемые компетентностные задачи должны быть практико-ориентированными задачами. Это приводит не только к необходимости проецировать такие практико-ориентированные задачи на каждую дисциплину и формулировать результаты обучения в терминах решения этих задач, но и выстраивать траектории обучения, среды, в рамках которых обучающиеся научаются решать эти задачи, двигаясь от простых задач к сложным, самостоятельно и в кооперации с другими обучающимися [1].
Есть много попыток создания таких интеллектуальных сред обучения, в которой обучающиеся самостоятельно выбирают свои траектории обучения, получают компетентностные задачи, решают их, получают обратную связь, корректируют свои решения, и самостоятельно добиваются достижения запланированных уровней. Но пока все эти среды нацелены на обучение программированию. Это связано с необходимостью четкой формализации модели предметной области, задач, отношения усложнения решаемых задач и с необходимостью предоставления среды оформления и формализованного анализа решений этих задач. Пока такие возможности могут предоставить только среды формальных языков программирования.
Есть отдельные виртуальные тренажеры, в которых также используются формализованные модели и отношения вложенности условий выполнения заданий. Например, тренажеры по управлению сложными техническими устройствами. Но они сложны, дорогостоящи и уникальны. И, наконец, есть целая индустрия компьютерных игр, в которых предусмотрено усложнение заданий, уровней игры и в которых происходит постоянное обучение игроков с фиксацией достигнутых уровней в очках и званиях.
Появление мультиагентных, нейросетевых моделей и технологий обработки данных и обучения машин, технологий создания программных систем на основе баз знаний позволяет ставить задачи по разработке интеллектуальной системы тестирования – обучения в произвольной технической предметной области [2]. Появляются примеры разработки таких систем и сред обучения, которые частично реализуют отдельные аспекты интеллектуальной среды обучения [4, 5, 6, 8, 9, 13]. Это позволяет надеяться на создание подобных эффективных систем обучения в недалеком будущем. Цель работы Формулирование подходов по созданию интеллектуальной системы тестирования уровней сформированности предметных компетенций, на основе которой можно сконструировать интеллектуальную среду автоматизированного обучения решению компетентностных задач. Конструирование математических моделей, с использованием которых можно построить процедуру автоматизированной оценки степени сформированности предметных компетенций, диагностировать ошибки в решении обучающегося. Решаемые задачи Исследовать существующие аналоги по созданию интеллектуальных сред контроля и обучения. Проанализировать их достоинства и недостатки.
Ввести формальную модель учебного модуля знаний, кейса и кейсового задания. Определить отношение усложнения на множестве кейсов. На основе отношения усложнения кейсов определить отношение частичного порядка на множестве типовых тестовых заданий, построить структуру на основе отношения усложнения заданий.
Сконструировать математическую модель уровня сформированности предметных компетенций обучающегося. Описать модель оценки уровня сформированности предметных компетенций. Исследование существующих аналогов Рассмотрим наиболее интересные с точки зрения применяемых моделей и технологий примеры реализации систем тестирования и обучения. Существующие системы тестирования сделали заметный шаг в направлении интеллектуализации. В современные системы тестирования вносятся элементы диагностики пробелов знаний. При конструировании и паспортизации тестового задания рассматриваются и анализируются не только используемые элементы знаний, но и возможные (типичные) ошибки при решении заданий. Выбор тестируемым определенного ошибочного ответа (дистрактора) связывается тестовой системой с типичной ошибкой и позволяет вызвать обучающую подсказку. Т. е. знания эксперта неявно встраиваются в блок оценки ответа учащегося. Также вводится уровневое тестирование, использование кейсовых заданий на самом высоком уровне сложности [3].
Таблица 1
Достоинства и недостатки существующих аналогов
| Характеристики обучающей среды |
Аналоги |
| Система интернет-тестирования и обучения «i-exam» |
LMS MOODLE, EDX |
Почти интеллектуальная система (ПИОС) |
HTML академия |
Среда организации соревнований
Black Box Challenge |
Игровые среды, стратегии экшны |
| Предоставляет возможность оформить решение задачи |
— |
± |
± |
+ |
+ |
+ |
| Оценивает ответ |
+ |
+ |
+ |
+ |
+ |
— |
| Автоматически оценивает решение |
— |
± |
— |
± |
+ |
+ |
| Анализирует ошибки обучающихся, выдает обратную связь |
± |
± |
± |
+ |
± |
± |
| Поддерживает диалог, обучает |
± |
± |
+ |
+ |
— |
± |
| Накапливает статистическую информацию об обучающихся |
+ |
+ |
+ |
+ |
— |
+ |
| Обладает адаптивностью к обучаемому |
— |
± |
+ |
— |
— |
+ |
| Оценивает и фиксирует уровень достижений |
± |
± |
± |
+ |
± |
+ |
| Обеспечивает управление обучением |
— |
+ |
± |
+ |
— |
— |
Также необходимо отметить бурный рост популярности и возможностей систем дистанционного обучения, таких как LMS MOODLE или систем открытого обучения, подобных open EDX. Они обладают всем необходимым потенциалом для организации автоматизированного обучения и сопровождения. Но многие возможности должны быть или отдельно настраиваемыми преподавателями или реализованы программистами в отдельно встраиваемых в систему модулях.
Некоторые модели адаптивного обучения «стараются» учесть слабую формализуемость и многокритериальность задачи обучения. Анализ предметной области обучения позволяет выбрать базовые элементы, которые представляют собой концепты для рассмотрения учебного материала. С учетом этих базовых элементов выделяют типовые операции – синтаксически, семантически и функционально завершенные процедуры действий над концептами. Обучение алгоритмам решения задач предметной области осуществляется через систему управления и контроля выполнения учебных задач [4].
Таким образом, следующим шагом в развитии современных автоматизированных обучающих систем (АОС) было явное выделение и представление знаний в виде различных моделей, методов, алгоритмов и технологий искусственного интеллекта [2, 4-6, 8, 11-13]. Появившиеся реально работающие обучающие системы, такие как ПИОС [5], способны отвечать на вопросы обучающихся и предъявлять обучающемуся задачи, которые кластеризованы по сложности. Вначале обучаемому предлагаются простые задачи, которые снабжены рекомендациями и указаниями. В случае необходимости, могут быть предложены и полные решения задачи. Сценарии обучения настраиваются гибко с помощью правил, учитывают психологические особенности обучающихся, уровень правильности ответов на тестовые задания.
В ПИОС автоматически формируется протокол прохождения как обучения, так и тестирования. Такой протокол позволяет анализировать, отлаживать процесс обучения и тестирования и является документом, служащим для разрешения различных разногласий между компьютерной системой и тестирующим. В системе используются два способа объяснения ошибок и материала. В одном из способов прогнозируются типичные ошибки на вопросы и на решения задач, и в случае их возникновения во время процесса обучения обучаемому предъявляются подготовленные заранее объяснения. Второй способ заключается в том, что строится база антизнаний, которая позволяет с помощью машины вывода дать развернутое объяснение ошибкам обучающихся. Для этого используют различные анализаторы, например, репертуарные решетки [5].
Надо отметить еще две важных характеристики, которыми обладают в полной мере игровые интеллектуальные среды и среды по обучению языкам программирования. Это возможность оформления и автоматический анализ решений и фиксация некоторых уровней достижений. Для вовлечения обучающихся в процесс обучения, для создания эффективных сред обучения эти характеристики являются также важными и должны учитываться при создании обучающих систем.
Из анализа существующих известных аналогов можно сделать вывод, что будущие среды обучения должны удовлетворять следующим требованиям:
- гибкость: поддержка существующих технологических стандартов обучения, расширяемость, возможность встраивания новых модулей по организации автоматизированной работы с обучающимися по аналогии с существующими развитыми LMS (англ. learning management system, система управления обучением);
- аналитичность: сбор необходимой статистической и аналитической информации о работе обучающегося для поддержки принятия решений по сопровождению, управлению обучением подобно тому, как это делают существующие развитые LMS;
- адаптивность: способность персонализации обучения, персональной подстройки процесса обучения, стимулирование и вовлечение, постоянный анализ и повышение эффективности тестирования и обучения аналогично тому как это реализовано в ПИОС и в игровых средах;
- интеллектуальность: поддержка диалога с обучающимся, предоставление возможности формулировки вопросов к системе обучения, конструирования решения задач в режиме обучения (с подсказками) и в режиме тестирования, обучение с использованием диагноза и анализа ошибок в решениях аналогично тому как это реализовано в игровых средах и, частично, в ПИОС и i-exam.
Наиболее практичным подходом по конструированию таких сред нам представляется подход, связанный с разработкой отдельных интеллектуальных модулей и встраиванием их в системы управления обучением (LMS). Факты успешного применения моделей, базирующихся на извлечении знаний из данных (data mining, knowledge recovering) на нейроматематике, нечетких множествах и нечеткой логике, на моделях марковских процессов при построении интеллектуальных и адаптивных рекомендательных и диалоговых систем также дают новые импульсы для применения этих и других новых моделей при построении обучающих систем [1, 2, 12-14]. Модель кейса и кейсового задания Проектирование современного процесса обучения использует понятия компетентностные компоненты и результаты обучения. Они составляют цели подготовки специалистов на разных уровнях обучения. Достижение некоторого уровня сформированности компетенций предполагает способность к решению определенного круга компетентностных задач, которые в рамках конкретной учебной дисциплины спроектированы на данную предметную область. Одна и та же компетентностная задача может решаться на разных уровнях сложности. Поэтому для автоматизации обучения необходимо создать среду, в которой обучающемуся предоставляются возможности решать компетентностные задачи на разных уровнях сложности, проверять свое решение и получать обратную связь с анализом отсутствующих или ошибочных компонентов решений и предоставлением рекомендаций по их конструированию.
Основная сложность перехода от формально-дисциплинарного к проблемно-активному типу обучения заключается в необходимости моделирования предметных сред. Задача эта является слабо-формализуемой. Отсюда и большое количество подходов к моделированию и самих моделей учебных задач. Здесь необходимо опираться как на экспертные модели описания компетентностных заданий – кейсов, так и на экспертные модели решения данных заданий. Полной формализации процедур построения всевозможных решений для произвольных предметных областей добиться очень сложно. Но можно попробовать создать операционное пространство, в котором эти решения фиксируются (логируются) и затем анализируются как с помощью экспертных систем с булевой логикой, так и с помощью различных аналитических систем с нечеткой логикой. Такое операционное пространство может содержать и описание операций, и описание понятий и концептов предметной области и отношений между ними [8, 9]. Такую модель предметной области можно использовать для создания оверлейных моделей обучения и обучающихся [11].
Введем понятие операционного пространства решения задач предметной области.
Обозначим перечень переменных – объектов модели учебной предметной области через X, множество функций, реализующих операции и некоторые предикаты через F, множество предикатов предметной области через P, через А обозначим множество примитивных и непримитивных абстрактных задач предметной области, через O - множество возможных операций с использованием которых решаются примитивные (базовые) абстрактные задачи, и базовые ситуации S, в которых детализированы условия, в которых решаются абстрактные задачи. Тогда под базовой моделью предметной области будем понимать 6-ку множеств:
`baseKM = {X, F, P, A, O, S}`
Такую структуру знаний, направленную на решение определенного круга (учебных) задач, будем называть базовой моделью учебного модуля (домен) знаний. Для этого в исходной структуре знаний выделены базовые знания, основу которых составляют примитивные задачи и операции, с помощью которых данные примитивные задачи решаются. Для описания множеств объектов и предусловий и постусловий выполнения операций используются понятия-предикаты [8, 9, 15].
Таким образом, базовый модуль содержит базу знаний о всех абстрактных задачах модуля A, понятиях–предикатах P, операциях O, функциях F, базовых ситуациях S (рис. 1). При описании ситуаций используется логика 1-го порядка. Даная структура создает фундамент для построения операционного пространства решения задач.
Базовый учебный модуль расширяется модулями экспертов, в которых описываются кейсы и методы решения кейсовых задач. Эксперты описывают сложные ситуации – кейсы, в которых решаются компетентностные задачи данного учебного модуля знаний. Формулировка метода звучит так: «чтобы решить эту задачу (достигнуть эту цель), нужно проверить выполнение определённого условия и выполнить декомпозицию решаемой задачи (решить последовательность подзадач)». Таким образом, задачей эксперта является свести решение задачи в исходной ситуации путем ее декомпозиции к более простым уже изученным ситуациям, в которых данная задача ранее уже решалась.
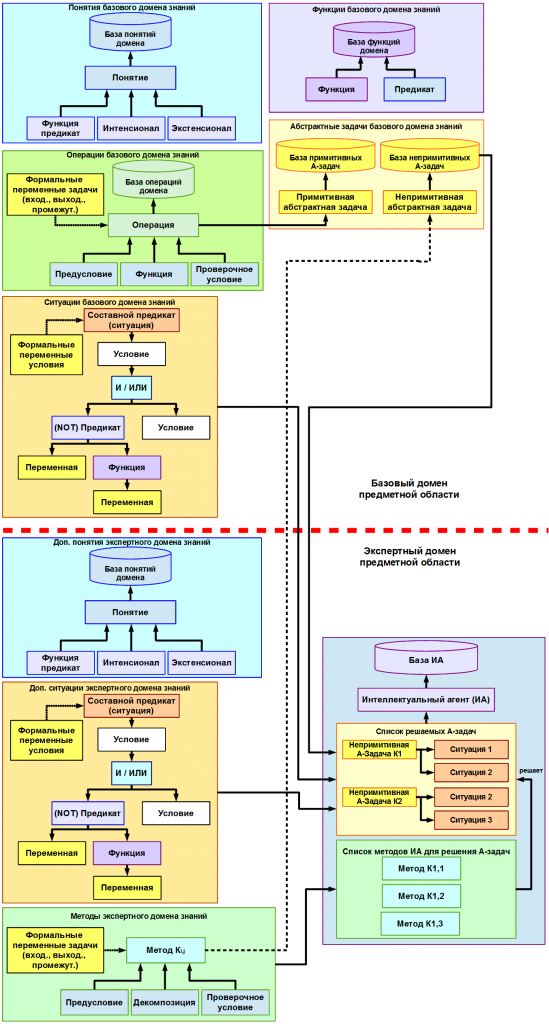
Рис. 1 Пример учебного домена знаний произвольной предметной области
Модель эксперта определяет, какие знания необходимы агентам для решения нетривиальных задач предметной области. Модель расширенного модуля знаний i-го эксперта выглядит так:
`KM(i) = (baseKM,{P_(i), S_(i), M_(i)})`
где baseKM – базовый модуль знаний предметной области;
Pi – дополнительные предикаты, введенные данным экспертом для описания предусловий выполнения методов;
Si – кейсы (ситуации), введенные данным экспертом для описания условий (предусловий и постусловий) применения введенных им методов;
Mi – методы, добавленные данным экспертом для решения нетривиальных абстрактных задач модуля знаний (которые не решаются посредством одной операции).
В дальнейшем описании мы будем использовать KM в качестве аббревиатуры для обозначения текущего операционного пространства - объединения базового модуля и всевозможных его экспертных расширений:
`KM = baseKM + KM(1) + ... + KM(k)+..`
Ситуации, описанные на языке предикатов, задают множества возможных значений переменных кейса и отношения между ними. Под кейсом будем понимать не любую, а некоторую типовую ситуацию, которая используется многократно при решении типовых учебных задач.
Например, при решении задачи сравнения двух натуральных чисел может встретиться одна из 4-х ситуаций (рис. 2). В самой простой ситуации мы можем ставить задачу сравнения одноразрядных чисел от 0 до 9. В более сложных ситуациях эти числа могут иметь несколько разрядов и различаться по количеству разрядов или иметь одинаковое количество разрядов и различаться или не различаться по 1-й цифре.
Для построения адаптивной системы тестирования мы заинтересованы в том, чтобы задать отношение усложнения на множестве типовых ситуаций. Модель структуры усложнения типовых ситуаций мы введем ниже. А сейчас рассмотрим модели типовой учебной задачи и кейсовой задачи.
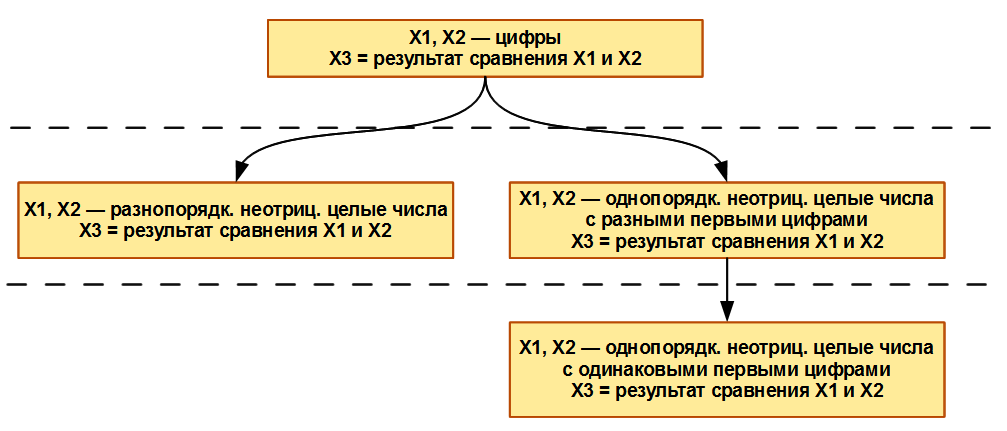
Рис. 2 Пример возможных ситуаций, встречаемых при решении задачи о сравнении двух натуральных чисел и задания отношения усложнения ситуаций
Под моделью типовой учебной задачи (ТУЗ) будем понимать кортеж из 4-х объектов [9]:
`TY3 = {X,S,A,IO}`
где X – подмножество объектов, участвующих в описании входных и выходных данных задачи;
A – решаемая абстрактная задача (А-задача);
S – типовая ситуация, в которой описываются исходные отношения между объектами, и, в которой предлагается решать данную абстрактную задачу; описание составляется на языке предикатов;
IO – описание входа-выхода задания: что дано и что надо найти; описание составляется на языке предикатов.
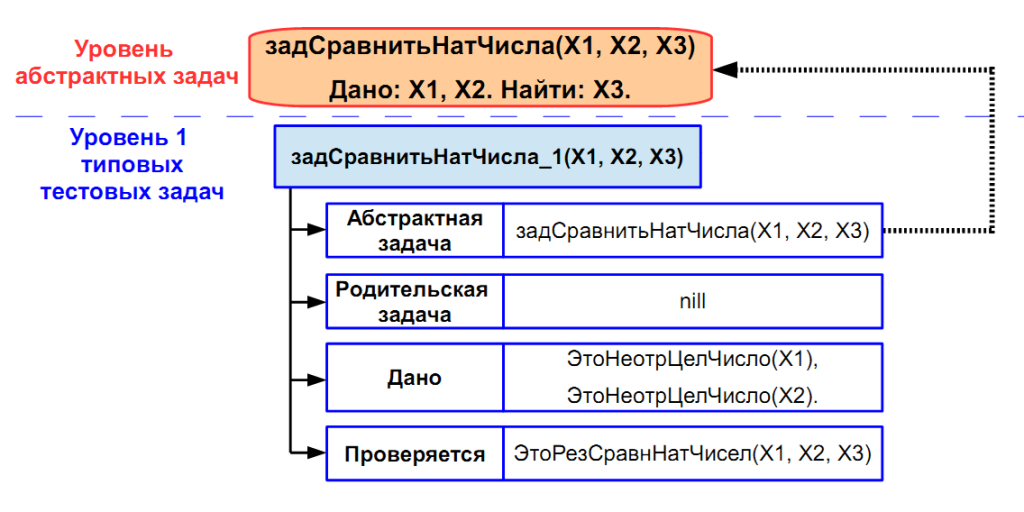
Рис.3. Структура описания типовой учебной задачи (ТУЗ)
Таким образом, в описании любой учебной задачи хранится ссылка на решаемую А-задачу, на ситуацию, уточняется что дано и какое условие должно выполняться в случае успешного решения задачи (рис. 3). Конкретизация типовых учебных задач осуществляется непосредственно при тестировании.
Под решением конкретного учебного задания (КУЗ - это ТУЗ в конкретной ситуации с конкретными исходными данными) в операционном пространстве KM будем понимать последовательность операций с исходными и промежуточными данными, при котором получается требуемый ответ, т. е. ответ, удовлетворяющий условию формулировки А-задачи, также формулируемый на языке предикатов. Т. е., если формулировка ТУЗ выглядит так:
Х = {x1, x2, x3},
S(pred) = (x1, x2 – разнопорядковые натуральные числа),
S(post) = (x3 – результат сравнения x1 и x2)
А = «найти результат сравнения двух чисел х1 и х2»,
IO = «Дано: х1, х2; найти x3»,
то решением является некоторая цепочка действий
`acts = <op_(1)(x1, x4), op_(2)(x2, x5), ... , op_(k)(x i,xj,x3)`,` `
приводящих к конкретизации x3, при подстановке которой в выражение S(post) получается ИСТИНА. Здесь под `op_k(x i, xj, x3)` понимается применение операции `op_(k)` к объектам, хранящимся в переменных `x i, xj, x3` . Решение может быть оформлено более подробно или менее подробно. Но, в любом, случае, это – цепочка операций, приводящих к конкретизации результата.
Результатом применения любой операции является конкретизация какой-то из участвующих в операции переменных. Таким образом, любую типовую задачу можно рассматривать как задачу удовлетворения ограничений, которые налагаются на переменные задачи её условиями. Описывая исходные данные типовой задачи, мы уже должны сузить множество значений входных переменных задачи, иначе можем получить большое множество возможных путей решений, которые будут сильно различаться по трудоемкости, сложности и используемым при решении операциям. Дальнейшее решение задачи должно планомерно сужать множество возможных значений выходной переменной задачи.
Данную ТУЗ будем считать кейсовой, если она подразумевает как минимум два разных рациональных, неизбыточных решения в операционном пространстве.
Такой способ описания типовых учебных ситуаций, типовых учебных задач, кейсовых задач позволяет сконструировать решетку усложнения тестовых задач и организовать адаптивное тестирование с учетом уровня сложности этих заданий. Формирование структуры типовых заданий Над данным операционным пространством естественным образом строится структура типовых учебных задач. База знаний конкретного учебного модуля содержит описание структуры учебных ситуаций. Простые ситуации описываются в виде отношений между переменными ситуации на языке введенных ранее понятий. Более сложные ситуации описываются как конъюнкции и дизъюнкции простых ситуаций (нормальные формы описания). При описании ситуаций используется их постепенное уточнение. При уточнении условий типовых учебных заданий естественным образом формируется структура ситуаций (рис. 4).
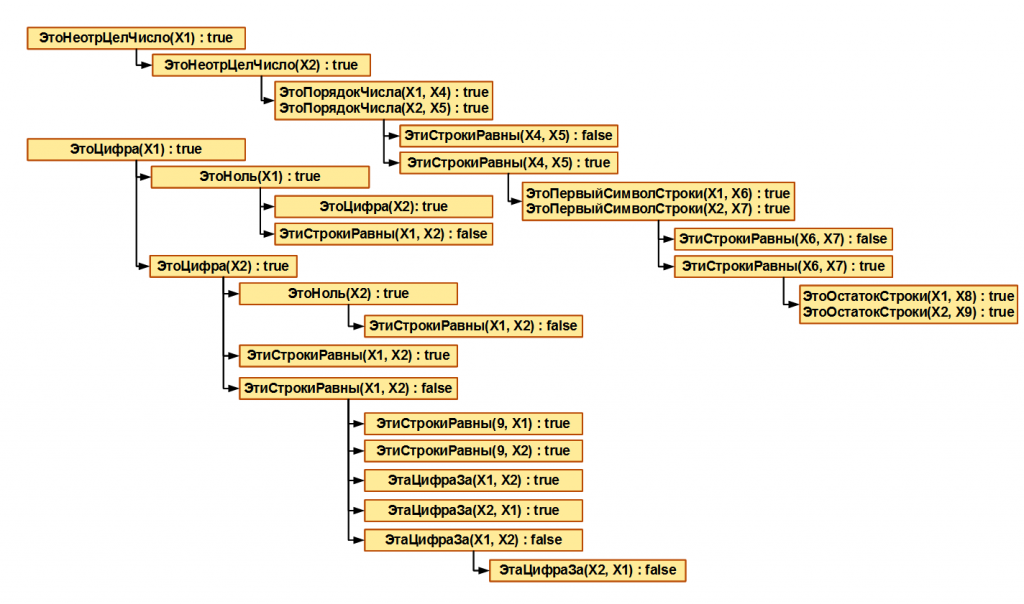
Рис. 4 Формирование структуры уточнения ситуаций при их описании
Описание учебных ситуаций с помощью отношения уточнения необходимо только для удобства и минимизации усилий по вводу и хранению базы знаний. При тестировании нам важно создать и использовать структуру постепенного усложнения ситуаций при предъявлении тестовых задач.
Для создания такой структуры вводится отношение частичного порядка усложнения ситуаций. Для этого явным образом задаются пары базовых ситуаций (s1, s2), удовлетворяющих данному отношению: s1 < s2 (рис. 5). Это явное задание индуцирует отношение усложнения составных ситуаций: s1&s3 < s2&s3, где s3 – произвольная ситуация. Явное задание отношения усложнения ситуаций должно выполняться экспертами и отражать тот факт, что решение задач в ситуации s2 сводится к решению задачи в ситуации s1. Например, если школьнику 2-го класса необходимо сравнить два натуральных числа одного порядка с одинаковыми 1-ми цифрами (173 < ? > 139), то эта задача будет сведена к задаче сравнения с разными 1-ми цифрами (73 < ? > 39). Аналогично рассуждая, можно прийти к выводу, что задача сравнения 173 < ? > 139 явно не проще, чем задача сравнения 17 < ? > 13. Таким образом, сначала надо научиться решать эту задачу в более простых ситуациях, а затем постепенно их усложнять.
Структура усложнения ситуаций (si < sj) индуцирует структуру усложнения типовых учебных задач, использующих данные ситуации в описании. Т. е. если имеется две типовые задачи – ТУЗ(i) и ТУЗ(j), в рамках которых решаются одинаковые А-задачи и условия которых соответственно совпадают с si и с sj, то если si < sj, то и ТУЗ(i) < ТУЗ(j). Данная структура усложнения типовых учебных задач образует алгебраическую решетку.
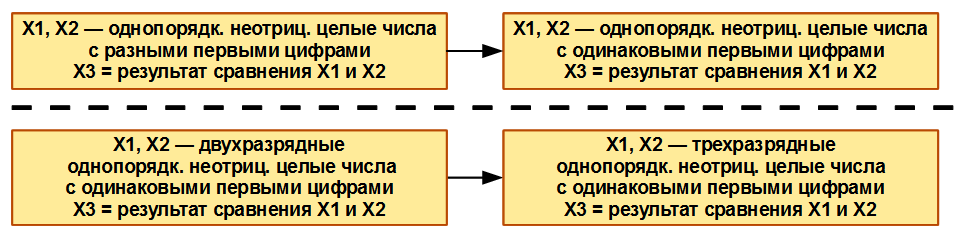
Рис.5. Явное задание отношения усложнения ситуаций
Можно заранее предсказать, что такое отношение усложнения задач будет гарантировать ухудшение (не улучшение) результатов тестирования с ростом сложности задач. Самое интересное, что наиболее известные практики тестирования уровней сформированности предметных компетенций (ЕГЭ, интернет-олимпиады) показывают, что чем более эффективными и результативными являются тесты, тем более выраженной является структура усложнения тестовых заданий [7, 10].
Ясно, что наиболее сложные задачи учебного модуля знаний и должны быть проекциями компетентностных задач данной предметной области. И эти задачи должны быть кейсовыми, т. е. предусматривать несколько возможных решений. Именно в этом и будет проявляться компетентность обучающегося – способность решать сложные задачи, выбирая практичные, т. е. рациональные решения. Одних знаний и умений здесь уже бывает недостаточно. Необходим опыт решения подобных задач, т. е. должна быть сформирована соответствующая компетенция.
Будем говорить, что базовый модуль знаний + экспертные модули + решетка усложнения ситуаций и тестовых заданий все вместе образуют учебный модуль знаний для данной предметной области. Для данной предметной области можно сконструировать несколько таких учебных модулей знаний [9]. Модель уровня сформированности предметных компетенций обучающегося Описание учебного модуля знаний позволяет сконструировать оверлейную математическую модель уровня сформированности предметных компетенций обучающегося.
Некоторые исследователи под моделью обучаемого понимают всю необходимую для релевантного обучения информацию: цель обучения; знания обучаемого (текущий профиль, состояние обучения или проекцию знаний обучаемого на модель предметной области); методику обучения и контроля; правила адаптации или правила изменения модели обучаемого по результатам обучения; начальную настройку [13]. Наша задача проще: нам важно, чтобы эта модель была адекватной с точки зрения того, что на ее основе можно было бы предсказать какие задачи обучающийся и на каком уровне сложности может решать, какие у него есть пробелы знаний и чему надо научиться для решения компетентностных задач. Такая модель может служить основой и для построения адаптивной системы тестирования и адаптивной системы обучения.
Модель обучающегося в рамках некоторого учебного модуля знаний предлагается строить, основываясь на структуре усложнения типовых ситуаций и тестовых заданий.
В модели обучающегося содержится следующая информация: сколько раз определенная А-задача встречалась в процессе решения в данной типовой ситуации TaskCase.nAll; сколько раз задача была верно решена в данной ситуации TaskCase.nTrue; Сколько раз задача была решена рационально с точки зрения k-го критерия в данной ситуации TaskCase.nOptimCrit(k) [8, 9]. В соответствии с данными величинами рассчитывается и заполняется карта сформированности предметных компетенций обучающегося в виде степеней уверенности верности следующих высказываний (рис. 6):
P(«Обучающийся умеет решать А-задачу Task в ситуации Case»):
`p(Task,Case) = (TaskCase.nTrue)/(TaskCase.nAll)`
P(«Обучающийся умеет решать А-задачу на i-ом уровне сложности»):
`p(Task, Case) = (sum_(Case.Level=i)p(Task, Case) * w(Case))/(sum_(Case.Level=i)w(Case)`
где `w(Case)` - вес важности данной ситуации при решении задач данной предметной области.
P(«Обучающийся рационально решает задачу Task в ситуации Case с точки зрения k-го критерия»):
`p(Task, Case, crit(k)) = (TaskCase.nOptimCrit(k))/(TaskCase.nTrue)`
P(«Обучающийся рационально решает задачу Task на i-ом уровне сложности с точки зрения k-го критерия»):
`p(Task, Case, crit(k)) = (sum_(Case.Level=i)p(Task, Case, crit(k)) * w(Case))/(sum_(Case.Level=i)w(Case)`
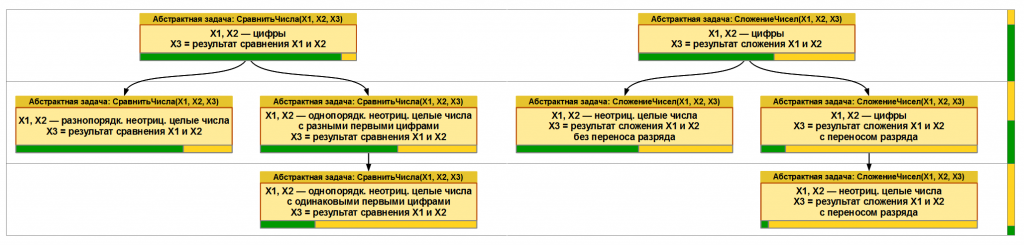
Рис.6. Пример карты уровней сформированности предметных компетенций обучающегося: выделено три уровня сложности типовых заданий; зеленым цветом отображается степень правильности решения тестовых заданий и степень сформированности предметной компетенции «способность выполнять операции с (натуральными) числами» на каждом уровне сложности.
Уровень сложности ТУЗ априори определяется, с одной стороны, на основании структуры усложнения ситуаций. Но с другой стороны, он должен уточняться экспериментальным путем, после получения результатов тестирования [7]. Полученная после обработки результатов байесовская решетка вложенности (усложнения) тестовых заданий должна сопоставляться с априорной решеткой и задачи примерно одного уровня решаемости должны находиться на одном уровней сложности в решетке.
На основании описанной модели можно сделать вывод о том, какие задачи на каком уровне сложности может решать обучающийся. Какие именно усложнения задач приводят к сложностям в решении. Отсюда можно вывести – в чем основная трудность и какие приемы и методы решения надо изучать в первую очередь. Свертку степеней правильности решения задач на одном уровне можно использовать как оценку сформированности компетенции на данном уровней сложности. Если взять в качестве порога успешного усвоения 70%, то по карте обучающегося можно будет сказать о достигнутом уровне сформированности данной предметной компетенции. Например, из рис.6 видно, что порог в 70% преодолен только на 1-м уровне сложности. Так что у обучающегося компетенция сформирована на некотором начальном уровне. Появляется возможность явно и задавать и явно диагностировать сформированность базового, продвинутого и экспертного уровней при подготовке обучающихся.
Такую модель сформированности уровней предметных компетенций у обучающегося можно назвать его компетентностной картой. Дополнительный учет рациональности решения задач с точки зрения различных критериев может дать информацию о способностях и предпочитаемых стратегиях решения задач данной предметной области, что может быть немаловажно при прогнозировании успешности решений более сложных задач, чем предъявленные ему на данный момент. Все это вместе формирует его карту способностей.
Для масштабируемости карты способностей можно использовать свойство аддитивности параметров модели. Показатели успешности решения вложенных задач могут суммироваться для расчета показателей успешности решения абстрактной задачи. Таким образом, на самом абстрактном уровне карта может свернуться до показателей успешности решения всех абстрактных (компетентностных ) задач данного учебного модуля знаний. Этот важный вектор может использоваться для понимания готовности обучающегося к изучению последующих дисциплин учебной программы. В свою очередь этот вектор может быть свернут до единственного значения – степени усвоения знаний данного учебного модуля. Заключение
Введено понятие учебного модуля знаний и операционного пространства для данного учебного модуля. В качестве фундамента построения операционного пространства рассматривается кортеж из множеств возможных объектов, решаемых абстрактных задач, используемых для их решения базовых операций и базовых ситуаций, описывающих условия применения различных операций. Для описания условий используются предикаты и функции. Такое базовое описание задает границы пространства описания возможных задач и возможных решений этих задач в виде последовательностей операций с объектами пространства. Подобные описания систем искусственного интеллекта не новы и используются, например, для организации сложных систем взаимодействия программных агентов и команд людей [15]. Основная сложность заключается в том, чтобы такое описание научиться использовать для анализа решений обучающихся и построения адекватной модели обучающихся, для создания системы, которая может и должна анализировать решения обучающихся, объяснять пробелы знаний и обучать решению компетентностных задач на разных уровнях сложности.
Введенное операционное пространство предлагается использовать для конструирования структуры усложнения тестовых (кейсовых) заданий и оверлейной модели уровня сформированности предметных компетенций. Система тестирования может использовать полученную решетку тестовых задач, описаний экспертами методов возможных решений для организации адаптивного тестирования и анализа возникающих проблем и локализации ошибок при решении задач. Введенные на операционном пространстве решений структуры данных могут адаптироваться в соответствии с поступающей информацией, чтобы быть адекватными. Операционное пространство решений задает язык, которым эти структуры описываются.
Одной из проблем создания подобных программных систем является их сложность. Система должна быть адаптивной и самоорганизующейся. Без этого свойства она быстро станет непрактичной в использовании. Появление новых парадигм создания программных и интеллектуальных автономных систем – нейросетевых, мультиагентных, обучающихся – делает эту задачу решаемой [12-14]. Интеллектуальная среда тестирования и обучения может быть гибко реализована в виде взаимодействия агентов – обучающегося, аналитика, тестировщика, эксперта, тьютора, и.т.п. Данная структура взаимодействия может иметь разные типы. Гибкость реализации взаимодействия достигается за счет заменяемости целей и ограничений действия агентов, а также за счет выбора и селекции типа самих агентов. Адаптивность среды может быть реализована за счет постоянного накопления и оформдения знаний через агентов-экспертов, агентов-аналитиков, других агентов и использования этих знаний для более детального анализа решений обучающихся, прогнозирования и оптимизации работы системы в целом.
References
1. Ramochnaya programma Evropeiskogo Soyuza po nauchno-tekhnologicheskomu razvitiyu № 7 (2007 – 2013 gg.). «Informatsionnye i kommunikatsionnye tekhnologii. [Elektronnyi resurs] URL: http://cordis.europa.eu/fp7/ict/ (data obrashcheniya: 01.07.2016).
2. Rybina G. V. Obuchayushchie integrirovannye ekspertnye sistemy: nekotorye itogi i perspektivy // Iskusstvennyi intellekt i prinyatie reshenii. 2008. № 1. S. 22-46.
3. Navodnov V. G. Kontseptsiya i tekhnologiya provedeniya Federal'nogo Internet-ekzamena v sfere professional'nogo obrazovaniya. / V. G. Navodnov, V. P. Kiseleva, A. N. Gubina, K. N. Kiseleva, O. V. Poryadina, V. V. Pylin, E. P. Chernova // Ioshkar-Ola: STRING, 2014.-59 s.
4. Galeev I. Kh. Adaptivoe obuchenie:pryamoi i obratnyi marshruty (ot znanii k navykam i obratno) // 31-ya mezhdunarodnaya konferentsiya MIPRO 2008 (komp'yutery v obrazovanii). Khorvatiya, Opatiya, 2008. S. 159-163.
5. Burdaev V. P. PIOS − pochti intellektual'naya obuchayushchaya sistema // Iskusstvennyi intellekt. 2009. № 4. S. 330-337.
6. Zhuikov I. V. Primenenie sistemnogo podkhoda pri sozdanii intellektual'noi sistemy testirovaniya urovnya usvoeniya znanii / I. V. Zhuikov, I. N. Nekhaev // Sovremennye problemy fundamental'nogo obrazovaniya v tekhnicheskom vuze. Ioshkar-Ola, PGTU, 2014. S. 144-148.
7. Krasil'nikov M. I. Issledovanie klassifikatsionnykh svoistv struktury testovykh zadanii, prednaznachennykh dlya otsenki urovnei sformirovannosti predmetnykh kompetentsii / M. I. Krasil'nikov, I. N. Nekhaev // «REGION: sistemy, ekonomika, upravlenie». Voronezh, 2011. № 4(15). S. 151-163.
8. Nekhaev I. N. Intellektual'naya sistema adaptivnogo testirovaniya urovnya usvoeniya znanii / I. N. Nekhaev, A. A. Vlasov // KII-2010. Dvenadtsataya natsional'naya konferentsiya po iskusstvennomu intellektu s mezhdunarodnym uchastiem (20 – 24 sentyabrya 2010 g., g. Tver', Rossiya). Sbornik trudov.-M.: Fizmatlit, 2010, T. 3, S. 257-263.
9. Nekhaev I. N. O podkhode k postroeniyu intellektual'noi sistemy diagnostiki probelov znanii / I. N. Nekhaev, I. V. Zhuikov // Informatsionnye tekhnologii v professional'noi deyatel'nosti i nauchnoi rabote. Sbornik materialov Vserossiiskoi nauchno-prakticheskoi konferentsii s mezhdunarodnym uchastiem.-Ioshkar-Ola, PGTU, 2014, S. 30-38.
10. Nekhaev I. N. O primenenii biklasternogo analiza rezul'tatov testirovaniya dlya otsenki urovnya sformirovannosti predmetnykh kompetentsii. / I. N. Nekhaev, M. I. Krasil'nikov, V. G. Navodnov, L. N. Sharafutdinova, A. A. Kolchev // Vestnik MarGTU, seriya «Ekonomika i upravlenie», T. 3., 2010. S. 20-32.
11. Avanskii S. M. Model' khraneniya dannykh i metod prinyatiya reshenii v komp'yuternoi obuchayushchei sisteme // Trudy Mezhdunarodnogo simpoziuma «Nadezhnost' i kachestvo». 2008, T. 1. S. 206-208.
12. Uglev V. A. Sistemnyi podkhod k formirovaniyu struktury i logiki raboty mul'tiagentnoi avtomatizirovannoi obuchayushchei sistemy // V Mezhdunarodnaya konferentsiya «Sistemnyi analiz i informatsionnye tekhnologii». Krasnoyarsk: IVM SO RAN, 2013. T. 1. S. 299-303.
13. Shana Makha Akram, Avtomatizirovannaya informatsionnaya sistema adaptivnogo obucheniya na osnove kompetentnostnogo podkhoda: diss. na soiskanie uchenoi stepeni kand. tekhn. nauk: 05.25.05 / Shana Makha Akram – Nal'chik, 2014. 182 s.
14. Roger Nkambou Intelligent Tutoring Systems (Guest Editorial) // Educational technology & Society – 2010-V. 13-N 1.-S. 1-2.
15. Potter, S., Tate, A. and Dalton, J. (2003) I-X: Task Support on the Semantic Web, Poster Abstract, Second International Semantic Web Conference (ISWC-2003), Sanibel Island, Florida, October 2003.
|
















 This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

