The Regression Method of Reducing the Boundary Equation to the Cauchy Problem When Modeling Chemical Fiber Treatment

Kalabin Aleksandr Leonidovich Doctor of Physics and Mathematics professor of the Department of Computer Software at TvSTU (Tver State University) 170026, Russia, Tver Region, Tver, nab. Afanasiya Nikitina, 22 kalabin@tstu.tver.ru

Udalov Evgeniy Vadimovich head of the Division of Enterprise Development at GUTA BANK 170100, Russia, Tver Region, Tver, Tverskoi prospekt, 6, of. 220 evgeny.udalov@mail.ru

Особенности элонгационного течения тонких неизотермических струй расплавов полимеров заключаются в сопутствующих ему процессах диффузии и теплопереноса ^[1]. При охлаждении расплава полимера существенно увеличивается его вязкость и могут начаться процессы стеклования или кристаллизации. Увеличение вязкости значительно влияют на характеристики движения. Однако неравномерность течения при растяжении и изменение радиуса струи влияют на взаимодействие струи со средой движения и интенсивность протекания всех процессов диффузии и теплопереноса.

Практической задачей, в которой применяются результаты изучения элонгационного течения струй расплавов полимеров, является производство (формование) синтетических волокон ^[2]. Для использования математических моделей на практике разработана программная система, так как, во-первых, процессы формования описываются нелинейными уравнениями с подвижной границей, требующие численного решения ^[3,4]; во-вторых, отдельные программные блоки используются многократно; в-третьих, для структурирования целесообразно сведение в базу данных исходных данных различных видов формования, используемых элементов схем технологического процесса, свойств расплавов полимеров.

В гидроаэродинамике используется система уравнений неразрывности, движения, теплообмена и состояния, которые отражают законы сохранения массы, импульса и энергии ^[1]. Отметим некоторые сложности использования системы общих уравнений для исследования элонгационного течения струй. Во-первых, настоящий уровень проведения эксперимента не дает возможность определить величины, входящие в краевые условия, например, распределение скорости или напряжения по радиусу. Во-вторых, из-за существенной нелинейности и большой размерности системы затруднена ее параметрическая идентификация. В-третьих, из-за первой и второй проблем сложно провести достоверное сравнение результатов расчетов с экспериментом. Наконец, в-четвертых, возникают очевидные трудности при применении численных методов для решения системы большой размерности (более 30) с указанными граничными условиями. На данный момент времени это – не решенная полностью проблема. Для решения указанных проблем нами предлагается подход, который заключается в исследовании элонгационного течения струй путем редукции общих уравнений. Редуцированные (упрощенные) системы уравнений более доступны для решения, анализа, а также для них имеются реальные экспериментальные данные.

На основе допущений для описания элонгационного течения тонкой струи из уравнения Навье-Стокса и краевых условий возможно получить одномерные уравнения движения и теплообмена –систему обыкновенных дифференциальных уравнений (СОДУ):

движения

v'' +{(μ1(T) – v' /v) + ρ1(v)}v' /μ2(T) + ρ2(v) /μ2(T)=0                                     (1)

теплообмена

T‘(x) = – α(v) [T(x) – TS (x)].                                                                         (2)

при v(0) = v0; v(L) = vL; T(0) = T0. Здесь v(x) – скорость волокна; T(x) – температура волокна; v' = dv/dx (штрих означает дифференцирование по x); ρi(v), μi(T) и  α(v) – функции от указанных аргументов.

Основные этапы работы программы моделирования формования химических волокон с приемным устройством это: ввод начальных условий (параметры технологического процесса, свойства полимера, свойства расчётной схемы), сплайн-интерполяция экспериментальных функций, расчёт (подбор начальных условий, решение СОДУ) и верификация решения.

При численном решении уравнения движения, являющегося обыкновенным дифференциальным уравнением (ОДУ) II порядка v”(v’, v, x)=0, необходимы начальные условия v(0)и v’(0).  Однако из известны лишь граничные значения v(0) и v(L). Возникает задача перехода от краевой задачи к задаче Коши. Поэтому в работе будут рассмотрены алгоритмы нахождения v’(0) по известному значению v(L).

Для численного решения краевых задач применяют метод стрельбы или иные методы, которые основаны на сведении краевой задачи к некоторой задаче Коши для той же системы уравнений ^[5,6].

Метод стрельбы (пристрелки) заключается в использовании левого краевого условия      и определении значения  с требуемой точностью по известному левому краевому условию .  Эта задача решалась методом дихотомии, аналогичный решению нелинейных уравнений. Он заключается в следующем. Определяется диапазон искомого значения  так, что их соответствующие значения vi(L) меньше и больше заданного значения v(L)= vL. Пара таких значений образует «вилку». Деля ее последовательно пополам до получения нужной точности, производим «пристрелку».  Для этого метода определены зависимости количества итераций от величины начального диапазона искомого значения начального градиента скорости (рис. 1, график 1) и количества шагов итерации от величины заданной точности поиска финишной скорости (рис. 2).

Можно представить теоретическую зависимость количество итераций N от величины начального диапазона искомого значения начального градиента скорости ΔV при заданной абсолютной погрешности y в виде

N=log2(ΔV)/v

Моделирование показывает удовлетворительное согласие этой теоретической зависимости и при   реальном моделировании (рис. 1, график 2).

2 1
Рис. 1. Зависимость количества итераций от величины начального диапазона искомого значения начального градиента скорости: 1 – численное моделирование; 2 – расчет оценки	Рис. 2. Зависимость количества итераций от величины заданной точности поиска финишной скорости

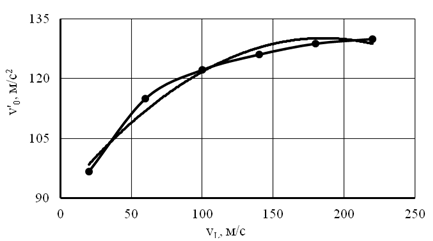
Рис. 3. Зависимость начального градиента скорости v’(0) от финишной скорости v(L): 1 – численное моделирование; 2 – уравнение квадратичной регрессии

Однако нахождение каждого нового значения функции v’0 требует численного интегрирования системы (1,2), т. е. достаточно трудоемко. Поэтому желательно использовать более быстрый метод, чем дихотомия. В ^[5,6] предложено еще несколько методов. Нами был протестирован аналог метода Ньютона. Однако он дал приблизительно такие же результаты, как и метод дихотомии (табл. 1).

В связи со значительным числом прогона модели (более 300 раз, отсюда число численного интегрирования более 3000) при ее реальном использовании на производстве необходима минимизации числа итераций. Для дальнейшего анализа при моделировании был построен график искомой функции