The use of artificial neural networks for the early diagnosis of diabetes

На сегодняшний день в мире диабет считается одним из наиболее распространенных заболеваний. Согласно данных Всемирной организации здравоохранения, около 350 млн. человек всех возрастов и рас страдают разными формами диабета ^[1]. Сахарный диабет не является следствием патологии какого-то конкретного органа, он возникает из-за общего сбоя в обмене веществ. Его признаки появляются со стороны органов и систем органов, наиболее чувствительных к этому процессу. Клинические признаки диабета зависят от типа заболевания, пола, возраста, уровня инсулина, артериального давления и других факторов. В работе рассматривается система ранней диагностики сахарного диабета обследуемого пациента использующая аппарат искусственных нейронных сетей.

Нейросетевые технологии призваны решать трудноформализуемые задачи, к которым, в частности, сводятся многие проблемы медицины. Это связано с тем, что исследователю часто предоставлено большое количество разнородного фактического материала, для которого еще не создана математическая модель. Хороший результаты показали модели искусственных нейронных сетей для диагностики психических расстройств ^[2], болезни Паркинсона ^[3] и Хантингтона ^[4]. Модели многослойных персептронов применяются для прогнозирования риска возникновения остеопороза ^[5]. Логический вывод и обобщенная регрессия использованы для диагностирования гепатита B ^[6].

Одним из наиболее удобных инструментов для решения подобных задач являются искусственные нейронные сети – мощный и одновременно гибкий метод имитации процессов и явлений. Современные искусственные нейронные сети представляют собой программно-аппаратные средства создания специализированных моделей и устройств и позволяют решать широкий круг задач диагностики на основе применения алгоритмов теории распознавания образов. Отличительное свойство нейронных сетей состоит в их способности обучаться на основе экспериментальных данных предметной области. Применительно к медицинской тематике экспериментальные данные представляются в виде множества исходных признаков или параметров объекта и поставленного на основе них диагноза. Обучение нейронной сети представляет собой интерактивный процесс, в ходе которого нейронная сеть находит скрытые нелинейные зависимости между исходными параметрами и конечным диагнозом, а также оптимальную комбинацию весовых коэффициентов нейронов, соединяющих соседние слои, при которой погрешность определения класса образа стремится к минимуму ^[7]. К достоинствам нейронных сетей следует отнести их относительную простоту, нелинейность, работу с нечеткой информацией, не критичность к исходным данным, способность обучаться на материале конкретных примеров. В процессе обучения на вход нейронной сети подается последовательность исходных параметров наряду с диагнозами, которые эти параметры характеризуют.

Для обучения нейронной сети необходимо иметь достаточное количество примеров для настройки адаптивной системы с заданной степенью достоверности. Если примеры относятся к разным диагностическим группам, то обученная таким образом искусственная нейронная сеть позволяет в последующем диагностировать и дифференцировать любой новый случай, представленный набором показателей, аналогичных тем на которых проводилось обучение нейронной сети. Несомненным достоинством нейронной модели является то, что при ее создании не нужно представлять весь набор сложных закономерностей описания диагностируемого феномена.

Вместе с тем, с применением нейронных сетей в практических задачах связан ряд трудностей. Одной из главных проблем применения нейросетевых технологий является заранее неизвестная степень сложности проектируемой нейронной сети, которой будет достаточно для достоверной постановки диагноза. Эта сложность может оказаться недопустимо высокой, что потребует усложнения архитектуры сетей. Простейшие однослойные нейронные сети способны решать только линейно разделяемые задачи ^[8]. Это ограничение преодолимо при использовании многослойных нейронных сетей.

В данной работе использовалась модель многослойного персептрона (нейронная сеть прямого распространения) обученная на основе алгоритма обратного распространения ошибки. В качестве активационной функции в работе, использовалась логистическая активационная функция (рис. 1):

`F=1/(1+exp(-alphaY)`

где ` alpha` – параметр наклона логистической функции.

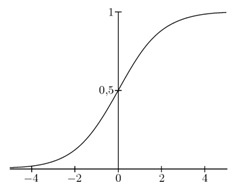
Рис. 1. Логистическая функция активации

Многослойный персептрон обладает высокой степенью связности, реализуемой посредством синаптических соединений. Изменение уровня связности сети требует изменения множества синаптических соединений или их весовых коэффициентов. Комбинация всех этих свойств наряду со способностью к обучению на собственном опыте обеспечивает вычислительную мощность многослойного персептрона.

Искусственная нейронная сеть содержала входной слой, один скрытый слой и выходной слой. Входной слой, нейронной сети, имеет 12 нейронов, выходной слой имеет два нейрона (рис. 2).

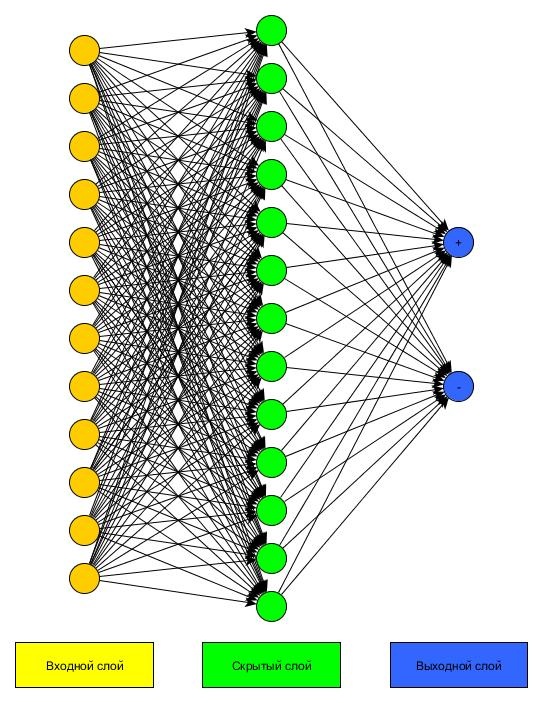
Рис. 2. Архитектура нейронной сети

Таблица 1. Параметры входного слоя нейронной сети

Для проектирования нейронной сети был использован пакет Neural Network Toolbox из MATLAB 8.6 (R2015b). Пакет представляет набор функций и структур данных описывающих функции активации, алгоритмы обучения, установку синаптических весов и др.

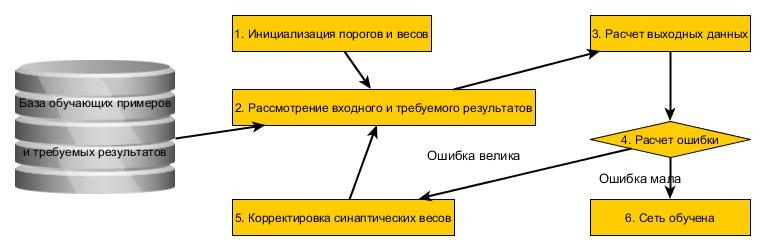
Рис. 3. Схема работы алгоритма обратного распространения ошибки

Алгоритм обратного распространения ошибки (рис. 3) предполагает вычисление ошибки, как выходного слоя, так и каждого нейрона обучаемой сети, а также коррекцию весов нейронов в соответствии с их текущими значениями. На первом шаге данного алгоритма веса всех межнейронных связей инициализируются небольшими случайными значениями (от 0 до 1). После инициализации весов в процессе обучения нейронной сети выполняются следующие шаги:

• прямое распространение сигнала;
• вычисление ошибки нейронов последнего слоя;
• обратное распространение ошибки.

Прямое распространение сигнала производится послойно, начиная со входного слоя, при этом рассчитывается сумма входных сигналов для каждого нейрона и при помощи функции активации генерируется отклик нейрона, который распространяется в следующий слой с учетом веса межнейронной связи согласно. В результате выполнения данного этапа мы получаем вектор выходных значений нейронной сети. Следующий этап обучения – вычисление ошибки нейронной сети как разницы между ожидаемым и действительным выходными значениями.

Полученные значения ошибок распространяются от последнего, выходного слоя нейронной сети, к первому. При этом вычисляются величины коррекции весов нейронов в зависимости от текущего значения веса связи, скорости обучения и ошибки, внесенной данным нейроном. После завершения данного этапа шаги описанного алгоритма повторяются до тех пор, пока ошибка выходного слоя не достигнет требуемого значения.

База обучающих и тестовых данных содержала 486 записей о пациентах, 243 из которых имели клинически установленный диагноз «сахарный диабет», другая часть пациентов была здорова.

Нейронная сеть была обучена на 240 выборках и протестирована на 146 выборках. Чувствительность разработанной нейросетевой модели составила 89.5%, специфичность 87.2%. Некоторая сложность теоретического обеспечения использования, трудоемкость и временные затраты по моделированию и обучению нейронных сетей компенсируется простотой их применения конечным пользователем. Если задача создания конкретной нейронной сети адекватной поставленной задаче и ее оптимальное обучение доступна лишь специалисту, то ее практическое применение конечным пользователем требует только навыков владения компьютером. Сложность интерпретации системы знаний обученной нейросетевой модели, является ненужной пользователю нейронной сети, так как для большинства конечных пользователей важно не понимание сущности работы нейронной сети, а ее результативность, информативность, безошибочность и быстродействие.