Prospects for the use of machine learning techniques in processing large volumes of historical data

Понятие «добыча данных», или «интеллектуальный (глубинный) анализ данных» (Data Mining) сегодня известно не только специалистам. И это не удивительно: после семинара, организованного в 1989 г. американским ученым российского происхождения Григорием Ильичем Пятецким-Шапиро (род. в 1958 г. в Москве) идея, что в больших базах «сырых данных» можно с помощью специальных алгоритмов отыскивать интересные знания, была воспринята с большим энтузиазмом, а исследования в этом направлении получили широкую популярность. Впечатляющая возможность найти что-то новое и полезное в уже имеющихся информационных массивах на протяжении уже более чем двух десятков лет увлекает научную фантазию большого числа исследователей и инженеров во всем мире. В результате этой деятельности на свет появилась целая плеяда готовых к применению коммерческих продуктов, предназначенных для анализа больших объемов неструктурированных, либо мало структурированных данных с целью нахождения новых, нетривиальных, полезных знаний и ранее неизвестных закономерностей. Эти новые знания призваны оказать так называемую «поддержку решений», помочь проанализировать разного рода риски, выявить ранее неочевидную функцию зависимости значения одного атрибута данных от значений других атрибутов ^[1].

Появление таких возможностей стало закономерным итогом развития многих отраслей науки и технологий. Например, еще в 1970-1980-е гг. был создан необходимый математический и алгоритмический задел, который позволил впоследствии применить алгоритмы математической статистики, теории вероятности и вычислительные методы к анализу больших массивов данных. Постоянное совершенствование технологической базы привело к тому, что на переднем крае науки, особенно в астрономии, физике, биоинформатике, других прорывных научных направлениях, а также в ряде секторов современного бизнеса объективно возникли огромные массивы информации, которые физически нельзя было обработать традиционными методами. Задача освоения этих данных сама по себе стала научным вызовом.

Широкое распространение систем управления базами данных (СУБД) позволило без особого труда внедрить в 1990-е гг. технологии аналитической обработки информации в режиме реального времени – так называемые OLAP-инструменты (от англ. online analytical processing), что открыло возможность оперировать огромными информационными массивами.

В итоге в относительно короткие сроки был сформирован готовый комплекс инструментов, программных оболочек, языков программирования для статистического исследования. Все эти решения были реализованы в коммерчески успешных программных продуктах, которые получили большое распространение.

Что касается технологий машинного обучения (machine learning, далее – МО), то они связаны с развитием одноименной научной дисциплины, которая возникла еще в конце 1950-х гг. Речь идет о создании и исследовании компьютерных моделей и алгоритмов, способных к «самообучению» на основе поступающей информации. Эти технологии в принципе во многом схожи с обычными методами анализа данных, но, как следует из названия, ключевое отличие заключается в процессе «обучения», которого нет в классическом статистическом анализе. Используя технологию обучения алгоритма, мы отталкиваемся от предположения об «однородности» данных, то есть от гипотезы, что во всех выборках (подмножествах) данных проявляются одни и те же зависимости между атрибутами, а распределение значений атрибутов не изменяет своего характера на всем множестве входных данных. В итоге появляется возможность «обучить» некий алгоритм, который впоследствии может быть применен к новым наборам данных без дополнительных ресурсоемких вычислений.

Таким образом, суть машинного обучения заключается в том, чтобы «научить» алгоритм верно сопоставлять набор входных параметров и соответствующий результат. При этом алгоритм не программируют заранее, какой результат выводить при поступлении тех или иных данных, а именно обучают в процессе. В качестве примера можно привести такую аналогию: представим, что входные параметры – это производственное сырье разного качества, а результат - описание продукта, который должен получиться из этого сырья. Допустим также, что для производства имеется один станок с двадцатью параметрами конфигурации, при этом конфигурацию необходимо задать до начала процесса один-единственный раз. Таким образом, смысл задачи - подобрать конфигурацию станка таким образом, чтобы из любого поступающего сырья были в итоге произведены продукты максимально соответствующие описанию. Аналогичные задачи подбора параметров решают при помощи алгоритмов машинного обучения.

В зависимости от особенностей задач и технологий обучение алгоритма может представлять собой четко выделяемый, ограниченный во времени этап, а может быть бесконечным процессом (онлайн обучение). В последнем случае необходимо определить некую стадию эволюции алгоритма, позволяющую сказать, что он теперь «минимально обучен» и с данного момента способен производить корректное соответствие выходного результата входным параметрам с заданной точностью ^[2].

Подобная парадигма естественным образом стимулирует развитие идей о возможности применения машинного обучения для моделирования («предсказания») будущего. Логично предположить, что если алгоритм «обучен» на основании большого массива данных о поведении некой системы в прошлом (например, экономики или государства в целом), то можно попытаться использовать его для моделирования будущего поведения этой системы на определенном интервале времени. Другими словами, появляется возможность прогнозировать траектории развития, вероятность и характер наступления кризисов в текущих исторических условиях, обучив алгоритм на примерах прошлого.

Применение технологий машинного обучения не ограничивается задачами, связанными с моделированием будущего. С равным успехом они помогают восстановить или аппроксимировать неизвестную функцию y=f (x), которая определяет, какой результат (значение функции y) соответствует входным параметрам (аргументу x). Важно, что природа и характер входных параметров или результата могут быть при этом сколь угодно разнообразными . Например, такие методы позволяют решать задачу классификации событий, основываясь не на хронологии (времени) их наступления, а исключительно на качественных параметрах (содержательное сходство, регион, действующие лица, исторический контекст), используя виртуальную функцию близости событий. В этом случае обучающая выборка (данные о событиях и их гарантированная классификация) будет основана на экспертных оценках.

Таким образом, независимо от конкретных способов машинного обучения, «обучаемые» алгоритмы можно разделить на две большие группы:

- алгоритмы с предсказывающей способностью;

- алгоритмы выявления закономерностей в данных.

Предметом настоящего исследования является анализ возможностей алгоритмов МО применительно к обработке «больших исторических данных» в целях определения путей дальнейшего развития междисциплинарной информационно-аналитической платформы «История современной России» (URL: http://prohistory.ru), далее – ИАП или ИАП «История современной России»).

Популярность машинного обучения

Технологии машинного обучения стали чрезвычайно популярными, благодаря ряду успешных проектов, в результате которых были созданы такие известные сегодня продукты, как алгоритм ранжирования Pagerank от корпорации Google, алгоритм рекомендаций Cinematch от крупнейшего дистрибутора медиа-контента Netflix, библиотека алгоритмов обработки изображений («компьютерного зрения») с открытым программным кодом OpenCV и др. Достижения этой научной дисциплины буквально прорвали технологические и психологические барьеры, которые стояли на пути реализации идеи о возможности более глубокой «переработки» уже существующих информационных массивов с целью извлечения из них нового ценного знания.

Благоприятная среда (доступность методологии, удобные инструменты) стимулировала творческую фантазию разработчиков в применении методов машинного обучения к решению самых разнообразных и сложных задач. Благодаря масштабному распространению информационно-коммуникационных технологий, методы МО давно вошли в повседневную жизнь интернет-пользователей. Например, алгоритмы машинного обучения уже лет десять помогают фильтровать нежелательную электронную корреспонденцию (спам). Среди других задач, с которыми успешно справляются алгоритмы МО, можно назвать, например, идентификацию взлома аккаунтов пользователя (осуществляется на основании сравнения шаблонов (паттернов) поведения обычных зарегистрированных пользователей и пользователей, чьи аккаунты были скомпрометированы) или создание контекстной рекламы (автоматическое формирование рекламных объявлений с учетом контекста открытой интернет-страницы, анализа пользовательской активности, обработки истории потребления контента и пр.). Еще один пример: интернет-сервис, задачей которого является соединение заказчика и исполнителя (всевозможные биржи товаров и услуг). В таких проектах прибыль извлекается из процента с продаж услуг/товаров с соответствующим финансовыми гарантиями и поддержкой центра урегулирования конфликтов, поэтому интернет-биржа не заинтересована в установлении прямых контактов между покупателем и продавцом, когда ресурс используется как площадка для объявлений, а сами транзакции проводятся «на стороне». Для профилактики такого рода эксцессов интернет-биржа с помощью алгоритмов МО отслеживает все коммуникации и вмешивается в процесс в случае выявления подозрительных сообщений/шаблонов

Следующим логическим шагом в распространении алгоритмов МО стало создание платформ SaaS (от англ. software as a service – «программное обеспечение как услуга»), на которых разработчик размещает созданный им программный продукт, обеспечивает его полное обслуживание и централизованное развитие, а заказчики получают доступ к программному ядру через Интернет, а также различные типы облачных сервисов. Например, в дополнение к инструментарию работы c «большими данными», хранящимися в облаке с использованием NoSQL-технологии ^[3] создания хранилища данных Google BigQuery, предоставляется сервис обработки этих данных алгоритмами машинного обучения Google Prediction API. В платформу облачных сервисов корпорации Microsoft для разработки приложений Azure также включен сервис Azure Machine Learning Center. Благодаря подобным решениям, ученый-исследователь получает возможность максимально быстро провести вычислительный эксперимент, применить алгоритмы МО, проанализировать качество обучения и степень полезности полученных результатов.

При этом важно понимать, что сами алгоритмы и программная платформа их исполнения являются лишь удобным инструментом, которые сами по себе не гарантируют получение значимого научного результата. Подлинно ценные знания могут быть получены на пересечении оригинально поставленной задачи, интересного массива данных и творческого применения алгоритмов МО для их обработки. Именно такое понимание смысла и возможностей использования инструментария МО культивируют сервисы, подобные Prediction API и Azure.

От экземпляра – к онлайн-алгоритмам

Основа машинного обучения - данные, представленные в виде множества так называемых «прецедентов». Под прецедентом обычно понимают некоторый минимальный, атомарный набор данных, чаще всего пару:

{экземпляр, результат}

Экземпляр – это объект, набор входных значений атрибутов. Именно на этих входных значениях происходит обучение алгоритма таким образом, чтобы каждому экземпляру алгоритм возвращал максимально «подходящий» результат.

В свою очередь, результатом может быть некоторая простая структура, например, число (определение стоимости недвижимости по параметрам) или имя (идентификатор) группы, к которой относится объект на входе при решении задачи классификации. Нередко результат может представлять собой сложную структуру, такую как граф или таблицу данных. Пример прецедента, где указаны экземпляры и результаты, приведен в Таблице 1.

Таблица 1. Пример прецедентов для машинного обучения

В общем случае, залог успеха машинного обучения связан с доступом к как можно большему количеству входных данных. Имея практически неограниченный запас входных данных, можно эффективно применять методы МО и достигать высокого качества работы алгоритмов. Именно поэтому наиболее активно алгоритмы машинного обучения внедряются на всевозможных интернет-сервисах, поскольку там гарантированно можно получить доступ к большим объемам данных.

Необходимо отметить наличие существенной разницы в природе данных современных интернет-сервисов и классических корпоративных баз данных, например, середины 1990-х гг. Корпоративные данные схожи с архивными, они не теряют своей актуальности, а соотношение текущей скорости поступления данных к объему уже накопленных относительно невелико. Особенностью интернет-сервисов является их пребывание «в потоке» непрерывно поступающих новых данных, например, о том, какой контент в данный момент выбирают посетители ресурса, чем они пользуются и что предпочитают. Актуальность таких данных постоянно меняется, и сама эта изменчивость является фактором, который дает возможность «переобучать» уже «обученные» алгоритмы. Представим себе, что мы имеем дело с сервисом рекомендаций фильмов, алгоритмы которого «обучены» на статистике просмотра пользователями фильмов, например, пятилетней давности. Если в некий момент времени, на экраны выйдет эффектный ремейк старого фильма, либо появится яркая экранизация известного литературного произведения, то это событие приведет к массовому увеличению числа поисковых запросов, например, к предыдущим версиям нового кино, к фильмам в жанре экранизации и пр. Таким образом, возникает новый пользовательский тренд и, соответственно, новый поток данных обучит алгоритм по-другому классифицировать старые фильмы, обработанные ранее.

Специфика, связанная с наличием постоянного потока данных, привела к смещению «интереса» разработчиков и пользователей к так называемым «быстрым алгоритмам», способным эффективно обрабатывать огромные массивы информации, поступающие в реальном времени. Парадокс ситуации состоит в том, что с точки зрения вычислительной сложности «быстрые алгоритмы» на самом деле являются медленными, т.е. требуют больше времени для обработки того же объема данных. Однако логика этих алгоритмов такова, что они могут выполняться в параллельном режиме (в несколько потоков) одновременно на нескольких процессорах/компьютерах, поскольку входные данные предварительно разделяются на «пакеты», а результаты выполнения различных потоков легко и органично соединяются воедино. Используемая в данной технологии платформа распределенных вычислений Hadoop MapReduce - это классический принцип «разделяй-и-властвуй», применяемый в мире компьютерных алгоритмов ^[4]. Масштабное проникновение методов распределенных вычислений во все сферы «компьютерной жизни» и развитие вычислительной техники в направлении мультипроцессорности и «многоядерности» - это, своего рода, взаимоподдерживающиеся процессы. Эти технологии активно развиваются, стимулируя друг друга, поскольку повышение производительности работы ЭВМ и скорости обработки данных само по себе является большой ценностью, даже если речь не идет о необходимости потоковой обработки больших массивов информации.

Успешное применение методов машинного обучения для решения различных задач всегда ориентировано на потребности пользователя, на возможность получить такие результаты, которые будут понятны для восприятия и пригодны для содержательной интерпретации. Например, мы пытаемся восстановить функцию зависимости стоимости недвижимости от общей площади помещений. В простейшем случае задача обучения сводится к подбору параметров a и b целевой функции: y = a * x + b

где y – стоимость недвижимости в рублях, а x - размер площади в квадратных метрах, а коэффициенты a и b требуется определить.

Этот пример - простая иллюстрация применения методов машинного обучения. Разумеется, в приведенном примере поставленную задачу проще всего решить методами стандартного регрессионного анализа. Но на деле итоговая функция может быть «устроена» намного сложнее и учитывать целый набор важных социально-экономических параметров, относящихся к выбранному району застройки: уровень преступности, процент индустриальной застройки, средняя стоимость квадратного метра жилых помещений, процент ветхого жилья, темпы роста численности населения и т.п. Такая детальная функция будет более точно, чем уравнение регрессии, определять потенциальную стоимость жилья в том или ином районе, а также сможет учитывать качественные характеристики, например, некоторые тренды и нюансы, которые были заложены исследователем в саму обучающую выборку (в частности, тренд растущего спроса и завышенной цены на жилье в недорогих районах в условиях замедления развития экономики и пр.).

Результатом обучения алгоритма в приведенном примере является набор параметров функции. Однако возникает вопрос, какой реальный смысл скрывается за полученными данными, какие закономерности и тенденции на рынке недвижимости они отражают?

Таким образом, возникает проблема интерпретируемости результатов машинного обучения. Причем, в зависимости от сферы применения МО, возможность интерпретируемости результата может оказаться более ценной, чем сама способность алгоритма корректно сопоставлять результат входным данным. Эта интерпретируемость может быть реализована благодаря самой логике работы алгоритма ^[5].

Например, известный алгоритм k-ближайших соседей (англ. k-nearest neighbor algorithm - KNN) основывается на принципе «схожести объектов». Каждый раз, когда на вход алгоритму поступает новый объект, алгоритм находит один или k ближайших экземпляров, на основании чего принимается решение об отнесении текущего экземпляра к той или иной группе (классу) ^[6]. Благодаря этой логике, после обучения для каждого из экземпляров можно указать не только класс, но и список ближайших соседей, что является дополнительным подтверждением «законности» отнесения экземпляра к определенному классу. Собственно, степень родства объектов по параметрам их близости и становится предметом анализа исследователя, что позволяет сформулировать новые закономерности, которые обнаруживаются из возникшего в результате обработки данных набора классов.

Применительно к базам исторических данных можно построить следующий практический пример. Создается подборка электронных текстов из подлинных архивных документов (например, публикаций СМИ), содержащих информацию о неких событиях исследуемого исторического периода. В качестве предварительной подготовки данных, проведем автоматизированный семантический анализ текстов и выделим упоминаемые в них имена собственные: фамилии участников событий, названия организаций, политических партий, географические наименования и т.п. Необходимо также ввести «меру близости» - функцию расстояния между двумя событиями. Составим такую комплексную функцию, которая учитывает все параметры. Например, если в событиях участвуют одни и те же действующие лица, либо они происходят в одном и том же географическом месте, то такие события считаются более «близкими». Для достижения более точного результата мы можем также использовать принцип взвешенного голосования: для каждой из метрик использовать коэффициент, на который умножается значение при вычислении «расстояния» между событиями. Подбирая этот коэффициент, можно творчески регулировать «разделяющую силу» параметра, т.е. решать, исходя из представлений исследователя, насколько сильно то или иное изменение в значении параметра будет влиять на итоговый результат - отнесение объекта к тому или иному классу.

Решаем задачу классификации при помощи методов МО. Одновременно, подбирая набор коэффициентов, ищем результат с максимальным количеством классов, чтобы повысить эвристическую ценность метода. Анализ исследователем «картины» итоговой классификации может дать крайне интересные результаты. Например, изучение событий на рубеже некоторой критической точки (события октябрьской революции 1917 г. или августа 1991 г.) может выявить «центры активности» в преддверии этой точки, продемонстрировать на конкретных фактах явные и неявные «группы интересов» и «группы поддержки», найти связи между ними и пр. В процессе содержательного анализа ученый получает возможность не только видеть классы и содержащиеся в них объекты, но также список «ближайших соседей», которые определили решение об отнесении данного объекта именно к этому классу. Такие результаты дают новую объективную основу для эвристического и сравнительного анализа не только новых массивов исторической информации, но и давно известных исторических событий и фактов.

Рассмотренный выше способ интерпретации результатов машинного обучения основан на логике работы вычислительных алгоритмов. Другую возможность интерпретации предоставляет сама структура и природа выходного результата. Дело в том, что алгоритмы МО могут решать задачу классификации, разделять неструктурированный массив объектов на классы, вычислять для новых объектов простые зависимости (например, восстановление регрессии), определять логическое значение двухмерного пространства значений (логическое «да» и «нет»). Что еще более важно, алгоритмы могут работать и с результатами более сложных типов, часть из которых представляет собой структуры данных.

Одним из подобных «сложных типов» результатов является так называемое «правило». Простое правило обычно имеет вид:

Если условие A, то следствие B,

где условием A может быть любое логические условие, которое апеллирует к значениям атрибутов объекта (например, значение атрибута - «количество законопроектов, рассматриваемых на сессии» < 30).

Условие также может быть составным (с использованием логических операций «и» и «или»):

Если (A1 и A2) или A3, то следствие B

Кроме того, условие может использовать дополнительные специфические функции, например:

Если частота упоминания (A1) > 43.2 и A2, то следствие B.

Правило принято называть ассоциативным, если его следствие задает значение или диапазон атрибуту:

Если частота_упоминания («название и номер заседания») > 43.2 и «количество законопроектов, рассматриваемых на сессии» < 30, то «процент явки» < 30%.

Правила могут оперировать со сравнительными характеристиками значений:

Если частота_упоминания («название и номер заседания») больше среднего и «количество законопроектов, рассматриваемых на сессии» < 30, то вероятность срыва заседания высока.

Причем, более абстрактные правила могут нести для исследователя больше полезной информации, чем точные правила.

Ниже представлен пример правила, которое вполне может быть выявлено из набора данных, но эксперт вряд ли окажется в состоянии интерпретировать полученный результат:

Если частота_упоминания («название и номер заседания») >50 источников, то B

Очевидно, что без каких-то сравнительных данных сложно оценить значимость того факта, что некое заседание упоминается в 50 источниках цитирования. Логичным продолжением правил является такая структура, как «дерево».

На Рисунке 1 изображено дерево решений с выделенными терминальными узлами (D, E, F, G)

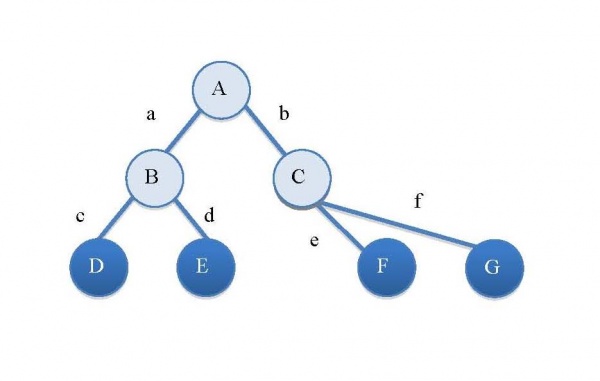
Рисунок 1. Дерево решений

В общем случае, результатом может быть граф, а дерево в данном случае – лишь частный случай графа. Дерево и правила тесно связаны: дерево всегда может быть представлено посредством правил. Например, дерево решений на Рисунке 1 может быть представлено в виде набора правил:

Если A есть a и B есть c, то D

Если A есть a и B есть d, то E

Если A есть b и C есть e, то F

Если A есть b и C есть f, то G

Деревья можно классифицировать в зависимости от того, какие утверждения «располагаются» в листьях дерева (терминальных узлах), а соответственно, что определяет само дерево. Распространенные варианты:

- если дерево определяет класс экземпляра, т.е. в терминальном узле указан класс, к которому относится экземпляр, то это «решающее дерево»;

- если в терминальных узлах определяются значения самого результирующего критерия, то это также «решающее дерево»;

- если дерево определяет значение одного или нескольких атрибутов, то это «ассоциирующее дерево»;

- по аналогии с локальными регрессионными правилами, в листьях дерева могут быть заданы функции значения результата или атрибута, тогда это «регрессионное дерево».

Все типы правил и деревьев являются достаточно удобными и эффективными с точки зрения способности человека к их органичному восприятию. Пожалуй, нет ничего более очевидного, чем простые правила, «если A_i, то B_i». Исследователям намного привычней видеть наборы правил, которые позиционируют следствия B в пространстве условий A_i, чем разбираться с безликими наборамицифровых коэффициентов. При этом, чем более равномерно набор правил или граф покрывает пространство условий A_i, тем более целостными и логичными эти правила представляются человеку.

На качество интерпретации результата, выраженного в виде правил или графа, влияет также степень так называемой нормализации. Понятие нормализации можно проиллюстрировать следующим образом. Пусть в некотором конкретном наборе правил используется совокупность условий A_i. Эти условия оперируют со значениями атрибутов и могут сколь угодно часто пересекаться, как по набору атрибутов, так и по их значениям, например:

Если A1> 0.4 и A1230, то …

Если A1>0 и A1<0.5 и A2<250, то …

В процессе нормализации можно минимизировать пересечение правил одного набора. Например, исключить упоминание и эксплуатацию некоторого атрибута A2 из всех правил набора, кроме одного. Также можно исключать пересечение по значениям атрибутов. Таким образом, в процессе нормализации возможно сокращение числа условий A_i за счет снижения качества результата, но со значительным повышением восприятия набора правил.

Одной из основ метода машинного обучения является оценка качества обучения. Качество обучения может быть проверено с использованием принципа разделения входных данных на обучающую выборку и выборку проверочную. После проведения процесса обучения, все данные из проверочной выборки поступают на вход «обученному» алгоритму, после чего вычисляется процент ошибок. Такой подход возможен, если данные или их часть имеют непустые записи в колонке «результат» напротив колонки «экземпляр». Другими словами, речь идет о методах «обучения с учителем» (англ. supervised learning - обучение «под присмотром» -), либо «частичного обучения с учителем» (англ. semi-supervised learning). Если же экземпляру изначально не сопоставляется результат во входных данных (т.е. применяются методы машинного обучения без учителя), то в этом случае необходимо ввести дополнительный критерий качества обучения. Например, решая задачу классификации, можно оценить количество классов, получаемых на выходе. Очевидно, что итоговое число классов не может быть слишком большим или слишком малым, оно должно попадать в некоторый оптимальный диапазон, который могут определить разработчики.

Возможно также применение и других критериев качества работы алгоритмов машинного обучения. Рассмотрим фазу оценки качества обучения. В некоторый момент работы алгоритма мы определяем качество обучения на основе специального критерия или соответствия результатам входных данных. Одной из классических является ситуация, когда на этапе оценки выявляется низкое качество работы алгоритма. В этом случае требуется пересмотр набора входных атрибутов, параметров самого алгоритма обучения, либо дообучение алгоритма на дополнительных наборах данных.

В случае применения алгоритмов МО к непрерывному потоку данных, например, поступающих в режиме онлайн, обычно исходят из представления об их одинаковой природе и неизменности статистических характеристик, то есть, из предположения, что распределения значений атрибутов не меняются. Что же произойдет, если наши допущения окажутся неверными, а статистические характеристики данных будут меняться во времени? Наличие неучтенной зависимости между распределением значений двух атрибутов полностью сводит «на нет» вероятность успешного обучения стандартных алгоритмов МО. Чтобы избегать такого рода рисков, специалисты советуют лучше «знать ваши данные», то есть выявлять и учитывать эти закономерности на этапе предварительной подготовки входных данных. Также рекомендуется предварительно проверять вероятность изменения характера распределения и дисперсии (рассеяния) значений атрибутов.

Что касается исторических данных, содержащихся, например, в хранилище информационно-аналитической платформы «История современной России», то их характерной особенностью является точная фиксация во времени (хронологическая определенность), конкретность источника происхождения (сообщения СМИ, официальные акты, мемуары современников и пр.), а также возможность изначально определить (например, на основе результатов, полученных «классическими методами» исторической науки) наличие неких трендов, внутренних зависимостей в данных того или иного исторического периода.

Такой информационный массив дает нетривиальные возможности, как для применения алгоритмов МО, так и для интерпретации полученных результатов.

Например, если провести обучение алгоритмов МО на выборке данных за некоторый период времени X, протестировать качество обучения и убедиться в его допустимом значении q₁, а затем применить алгоритм к данным за период Y, то, проверяя качество работы алгоритма на этих новых данных, мы получим значение q_2. Сопоставление q₁ и q₂ может характеризовать соответствие самих исторических периодов и содержащихся в них данных. Например, резкое падение качества q₂ по отношению к q₁ говорит, скорее всего, об изменении трендов, либо о том, что исторические процессы, существовавшие в период X, уже закончились и не проявляют себя в период Y. Можно предложить и другую интерпретацию этого результата: новые тенденции, возникшие в период Y, оказались настолько более значимыми для современников в сравнении с процессами, существовавшими в период X, что исторические источники перестали их упоминать, в силу чего алгоритм, обученный на выборке X, больше не работает в применении к данным из выборки Y.

Подобный подход можно условно назвать методом выявления трендов и их временных диапазонов. Другими словами, имеется возможность находить точки начала и окончания трендов по «аномалиям» работы алгоритмов машинного обучения. Причем, аномалии эти возникают естественным образом, исходя из следующей предпосылки: если алгоритм обучается по выборке данных c равномерным распределением значений атрибутов и константными взаимосвязями между атрибутами, то проверка работы алгоритма должна показывать высокий процент правильных результатов, определенный алгоритмом. После обучения и подтверждения успешной работы на тестовой выборке, можно применять алгоритм к данным иной выборки, качественно другого исторического периода. В этом случае, фиксируя падение качества работы алгоритма, можно уверенно говорить об изменении трендов ^{[7, 8]}.

На результаты применения методов МО в работе с историческими данными могут повлиять разные принципы выделения обучающих выборок. Например, эксперты могут предварительно разделить данные о неких исторических событиях по нескольким «тематическим» хранилищам – в одном будет содержаться информация о фактах исключительно политического толка, в другом – сведения, относящиеся к сфере экономики, в третьем – данные о событиях в сфере культуры. Один вариант действий - применить МО к выборкам из каждого хранилища по отдельности («обучить» алгоритмы только на политических данных или только на экономических). Другой вариант - «слить» все источники в единую базу, ввести некоторые параметры корреляции, чтобы согласовать данные разной природы и применить алгоритмы МО к объединенному множеству с целью учесть «слабые» взаимосвязи и выявить новые тренды ^[9].

Когда говорят о компьютерном анализе исторических данных, то неявно предполагается, что речь идет об анализе текстов. Однако, это далеко не так. Текст исторического источника «как он есть», не является объектом, который можно без предварительной подготовки автоматически обработать и извлечь «скрытые знания». Более того, в настоящее время специалистами в области цифровых гуманитарных наук (англ. Digital Humanities) создается все больше хранилищ исторической информации, в которых содержатся объекты самой различной природы – помимо полных текстов там размещаются аудио-, видео-, фотоматериалы, трехмерные модели артефактов, структуры аккаунтов социальных сетей и многое другое. В наши дни все эти объекты имеют значение в качестве исторического источника, но данные, пригодные к машинной обработке, необходимо предварительно подготовить (например, извлечь из полных текстов) и снабдить типизированным набором атрибутов.

Таким образом, одной из ключевых проблем в применении методов машинного обучения и анализа данных для решения задач исторических исследований является необходимость работать с «сырыми» исходными данными. В зависимости от природы и особенностей первичных данных источников, подходы к их подготовке и обработке могут меняться.

Полнотекстовые данные

Задача обработки «сырых» полнотекстовых данных (в данном случае – текстов исторических источников) не является на сегодняшний день чем-то из ряда вон выходящим. Одним из базовых подходов является анализ частоты вхождения слов в текст. Предварительно, из текста исключаются все служебные слова, не несущие смысловой нагрузки. Оставшиеся слова приводят к нормальной форме, отбрасывая различные частицы, указывающие на падеж, глагольное время, число и прочее (проводят процедуру так называемого «стемминга» - процесс нахождения основы слова). Порядок следования слов в тексте также не берется в расчет, однако слова упорядочиваются по некоторому правилу (например, длине слов и алфавиту). Такой поход может показаться слишком «грубым», но он значительно снижает вычислительную сложность и ресурсоемкость машинного обучения.

Если далее слова в «перемешанном» тексте обрабатываются в режиме «как есть» ( как множество объектов с дублями слов), то мы имеем дело с так называемой «кучей» (англ. heap) слов. Если же предварительно потратить время и составить карту «уникальное слово - количество вхождений», то речь будет идти о работе с так называемой «сумкой» (анг. bag) слов ^{[10, 11]}. В случае применения количественных характеристик слов («сумка») или набора и отсортированной последовательности слов («куча») возможно введение численных характеристик, таких как близость (установление параметров схожести) двух текстов, характер или эмоциональная «окраска» текста (введение классификации) и так далее ^[12].

Семантические графы

Качественно другой подход - анализ содержимого текста, основываясь на его смысле. Семантический анализ является вычислительно дорогой операцией, однако он позволяет выделить ключевые сущности, которые заключают основной смысл текста и являются предметом повествования. Выделение из текста вспомогательных и второстепенных субъектов, характеризует смысловой контекст и набор связанных тем. Собственно, этим и занимается компьютерная лингвистика, когда строит так называемые онтологии предметных областей. В процессе анализа происходит построение структуры семантического графа или дерева. Машинное обучение на данных этих графов может дать отличные результаты, основанные на «смысловой нагрузке» текстов.

Метаданные

Еще один принципиально иной подход анализа исторических источников связан с отказом от анализа полных текстов и попыткой выделения из них интересующих объектов с заданным набором атрибутов. Например, имея архив новостных лент информационных агентств, можно выделить в нем объекты с условным названием «события», обладающие такими атрибутами, как дата, место, участники (персонажи), характер (экономический, политический и т.д.). В этом случае выделение объектов «сыром» информационном массиве можно осуществить как при помощи семантического или статистического анализа, так и при помощи машинного обучения ^[13]. Аналогичные приемы могут быть использованы для работы с базами метаданных, относящихся к принципиально нетекстовым источникам (медиафайлы, трехмерные цифровые копии артефактов и пр.)

Минимизация количества атрибутов

Во всех разделах анализа данных уделяют особое внимание определению их атрибутов. Исходные данные заведомо избыточны, поэтому первичное количество атрибутов, которые можно выделить, как правило, огромно. Отсюда возникает задача минимизации количества атрибутов. С одной стороны, такая минимизация полезна для простоты восприятия результатов анализа: одно дело, попытаться охватить взглядом дерево ассоциаций, использующее 1500 атрибутов, другое дело – ограничиться двумя-тремя десятками атрибутов. С другой стороны, минимизация количества атрибутов значительно снижает вычислительную сложность, которая экспоненциально зависит от размерности пространства атрибутов. Таким образом, от успешности определения атрибутов зависит не только качество анализа, но и сама его физическая возможность и целесообразность.

В общем случае атрибуты (характеристики – англ. features) данных могут быть определены в рамках двух стратегий.

Первая стратегия предполагает выбор характеристик из всего их множества. Основная задача при этом заключается в выявлении характеристик, вносящих минимальный вклад в разнообразие данных, а значит, являющихся избыточными. Именно такие характеристики можно и нужно исключить из последующего анализа. Для реализации этого подхода выбирают одну или несколько количественных оценок, в результате характеристики с наименьшими оценочными значениями признаются избыточными.

Вторая стратегия – выделение характеристик, т.е. конструирование новых наборов характеристик, производных от уже имеющихся. Если первоначальный набор характеристик – это множество X, то при выделении создается качественно новый набор Y, где каждая характеристика является функцией от одной или нескольких характеристик из X. Таким образом, создаются новые комплексные характеристики, которые отражают сложные взаимосвязи между первичными характеристиками. В итоге, реализация этой стратегии позволяет значительно сократить количество характеристик в наборе.

Необходимо отметить, что в процессе определения набора характеристик также применяются алгоритмы машинного обучения. Таким образом, в процессе анализа больших массивов данных, метод МО эксплуатируется дважды: на этапе выбора характеристик и непосредственно в процессе обучения.

Временные ряды

Еще одним выгодным сценарием применения МО к анализу исторических данных является анализ временных рядов (англ. time series). Подобный анализ применяется к данным, среди атрибутов которых имеется непрерывная исчислимая величина (например, вещественное число), которое подлежит сравнению. Чаще всего, такой величиной является дата и/или время, а данные содержат избыточную хронологическую последовательность изменения состояния системы во времени. Классическими примерами временных рядов являются хронологически упорядоченные результаты наблюдений за изменением значения разного рода социально-экономических показателей - валового внутреннего продукта на душу населения, численности городских и сельских жителей, стоимость «потребительской корзины» и тому подобное. В работе с такого рода данными существуют две актуальные задачи: симплификация (упрощение данных для облегчения записи протекающего процесса меньшим набором данных) и аппроксимация (необходима для определения данных в недостающие моменты времени).

Данные исторических хроник представляют собой специфический случай временных рядов. С одной стороны, каждое событие истории уникально и потому с формальной точки зрения нельзя сказать, что в хрониках мы наблюдаем изменение некоего показателя во времени. С другой стороны, если хронологическая база является по-настоящему большой и непрерывной (т.е. на каждый день большого временного диапазона содержит огромное множество разнообразных данных о подлинных событиях), то фактически мы имеем дело с временным рядом, демонстрирующим хронологически упорядоченные результаты наблюдений за изменением состояния общественной системы в целом.

Задача симплификации идеально подходит для анализа подобных данных. Если избыточные временные данные – это набор исторических событий, то попытка описания всего процесса изменения состояний системы – это попытка вычленения наиболее значимых событий, которые и формируют образ исторического процесса. Поэтому в данном случае решение задачи симплификации представляет собой выделение из общего потока тех событий, которые имеют наибольшую важность и вносят в исторический процесс наибольший вклад.

Аналогичным образом задача аппроксимации может подсказать, какое событие в описанном временном ряду отсутствует и какими характеристиками оно должно обладать. Таким образом, в процессе решения подобной задачи алгоритмы машинного обучения открывают новые возможности поиска недостающих звеньев в едином историческом процессе и подсказать, как эти «звенья» должны выглядеть.

Как уже отмечалось, энтузиазм в применении методов машинного обучения для решения все большего количества прикладных задач поддерживается их прогностической эффективностью. Однако подобные возможности МО являются не столь актуальными для классических задач анализа данных, включая частный случай исследования больших массивов исторической информации. В этом контексте интерес, скорее, представляет способность математического аппарата, заложенного в методы машинного обучения, выявлять нечеткие взаимосвязи и тенденции в обрабатываемых наборах данных. В частности, речь идет о возможности восстановления неизвестной функции, которая позволяет заданным входным параметрам сопоставить некоторый результат. Какой бы сложной ни была искомая функция, МО надежно позволяет восстановить эту зависимость, если заданный ранее порог качества обучения был достигнут. Эти возможности как нельзя лучше соответствуют задаче выявления связей (англ. knowledge discovery), которая является сутью анализа данных в классическом понимании. Именно поэтому алгоритмы МО получили широкое распространение в исследованиях и прикладных пакетах обработки больших данных.

Требование обеспечить непрерывное измерение качества обучения в процессе МО способствует созданию механизма обратной связи, который позволяет на всех этапах контролировать, насколько «хорошо обучен» алгоритм. Благодаря такому подходу можно вовремя прекратить процесс обучения, который, по сути, является бесконечным. Кроме того, это позволяет контролировать степень достаточности обучающей выборки и управлять процессом переобучения. Такой контроль, в частности, позволяет обеспечить условие «сходимости» процесса обучения только при выявлении стабильной функции связи «вход-выход». Другими словами, алгоритм машинного обучения выявит взаимосвязь в данных и восстановит функцию связи только в случае, если эта связь будет главенствующей (самой сильной среди других «побочных» связей) и стабильной (проявляющейся на всех подмножествах всего многообразия входных данных). Данное условие гарантируется тем, что при любом его нарушении (например, искомая связь перекрывается шумами и выбросами или не прослеживается на определенных выборках входных данных) происходит падение качества обучения.

В результате этот эффект позволяет говорить о том, что метод машинного обучения способен выявить существующие взаимосвязи или продемонстрировать их отсутствие. При этом ситуация получения ошибочного результата (выявления «фантомных» связей и тенденций) практически невозможна. Такая гарантия от технических ошибок особенно важна в случае поиска неявных закономерностей в массивах исторических данных, поскольку исследователи-гуманитарии, как правило, испытывающие доверие к результатам «точных математических расчетов», способны выстроить убедительную интерпретацию фактически любых «фантомных зависимостей». Таким образом, залогом успешного анализа больших исторических данных является внимание к уровню точности выявляемых связей и зависимостей.

Развивая уже упомянутый сюжет о выявлении шаблонов и аномалий в массивах данных, можно отметить такое интересное явление, как возможность «прямого» и «непрямого» применения машинного обучения к анализу данных. Прямым применением методов МО является обучение алгоритмов с целью восстановления связи или классификации объектов. Восстановленная связь сама по себе является объектом для анализа в зависимости от метода представления. В частности, если связь представлена деревом ассоциаций, то по структуре этого дерева можно судить о разделяющей силе атрибутов, о характере выделенных групп, о степени корреляции между атрибутами в зависимости от частоты их упоминания вместе в узлах дерева. Например, можно анализировать, почему условие «если дата события находится в окрестности точки “август 1991” и место события «близко к Москве», приводит к ассоциирующему правилу «характер события – политический, исторический процесс – “августовский путч”».

Непрямой сценарий применения методов МО – это уже описанный ранее контроль качества обучения на различных выборках входных данных. Если на одних выборках обучение устойчиво показывает хорошее качество (назовем эти данные - данными из подмножества A), а на других низкое (подмножество данных B), то этот результат позволяет сделать вывод о различной природе данных, т.е. наличии качественно разных взаимосвязей в различных массивах. Согласно общей теории машинного обучения, подобная ситуация свидетельствует о наличии дополнительного атрибута данных, который не был учтен, но явно оказывает влияние при переходе от данных из A к B.

В случае решения методами машинного обучения прикладных задач технического характера, таких как распознавание образов, «компьютерное зрение», обработка звука или экономическая статистика, существует возможность составить список версий и путем их последовательной проверки точно определить, какой ранее неучтенный атрибут может быть «виновником» сложившейся ситуации.

В случае с большими историческими данными, такой механический «перебор версий» представляет значительную проблему. Поэтому анализ результатов обучения МО на разных выборках данных может оказаться единственным пригодным инструментом для выявления скрытых «агентов влияния». С учетом того, что количество данных в выборке A (или B) может быть очень значительным, а сам анализ осуществляется объектно-ориентированным методом МО (англ. instance-based learning), необходимо максимально точно определять «переходные» точки значений атрибутов. В этом случае математики говорят, что эти переходные точки образуют гиперплоскость в n-мерном пространстве атрибутов, по одну сторону от которой – объекты множества A, а по другую – множества B. Точное построение этой гиперплоскости крайне важно для последующего эвристического анализа факторов, оказавших влияние на разделение областей A и B.

Рассмотренные в исследовании методики и подходы, а также проведенное тестирование с использованием информации из хранилища данных платформы «История современной России» показали, что технологии машинного обучения имеют большой потенциал для анализа «больших исторических данных». Существующий мировой опыт применения алгоритмов МО к решению многих актуальных задач может быть успешно использован для создания и развития нового аналитического инструментария социальных и гуманитарных наук, в том числе в области истории современной России.