Methods of detection and spatial localization of groups of point objects

Рассмотрим сущетсвующие методы и подходы обнаружения и пространственной локализации групп точечных объектов, которые в качестве описательных признаков используют особые точки ^[1,2]. Существует множество алгоритмов для локализации такого рода точек. Так можно выделить класс методов, где особые точки поддвергаюся минимальным искажениям с течением времени, например, между соседними кадрами видеопоследовательнсти. Одним из наиболее распространенных типов особых точек являются углы на изображении, т.к. в отличие от ребер углы на паре изображений можно однозначно сопоставить. Детектор Моравеца ^[3] является самым простым детектором углов. Предлагается измерять изменение интенсивности пикселя I(x,y) посредством смещения небольшого квадратного окна с центром в (x,y) на один пиксель в каждом из восьми принципиальных направлений. Следует отметить, что данный детектор не является инвариантным относительно преобразования поворота и имеет большое число ложных срабатываний на ребрах вследствие шума. Детектор Харриса ^[4] строится на основании детектора Моравеца и является его улучшением, т.к. для него характерна анизотропия по всем направлениям. Харрис и Стефан вводят в рассмотрение производные по некоторым принципиальным направлениям, раскладывают функцию интенсивности в ряд Тейлора. Однако ему присущи некоторые недостатки, среди которых большая вычислительная трудоемкость (по сравнению с детектором Моравеца), чувствительность к шуму и зависимость результатов детектирования от масштаба изображения. Также здесь можно отметить алгоритмы нахождения особых точек, основанные на преобразованиях вейвлет ^[5], риджет ^[6], Хафа ^[7] и др.

Следующий класс обнаружителей особых точек, которые являются стабильными при смене освещения и небольших движениях объекта. Детектор MSER (Maximally Stable Extremal Regions) ^[8] решает проблему инвариантности особых точек при масштабировании изображения. Детектор выделяет множество различных регионов с экстремальными свойствами функции интенсивности внутри региона и на его внешней границе. Преимущества, которыми обладает детектор – это инвариантность к аффинным преобразованиям интенсивностей, устойчивость, одновременное детектирование областей разного масштаба и вычислительная эффективность. Описанные ранее детекторы определяют особые точки на изображении, в частности, углы, применяя некоторую модель или алгоритм напрямую обращаясь к пикселям исходного изображения. Альтернативный подход состоит в том, чтобы использовать алгоритмы машинного обучения для тренировки классификатора точек на некотором множестве изображений. FAST-детектор (Features from Accelerated Test) ^[9] относится к эвристическим алгоритмам и строит деревья решений для классификации пикселей. Он хорошо зарекомандовал себя при слежении за объектами в реальном времени.

В настоящее время существует ряд методик описания изображений по особым точкам, которые обладают высокой стабильностью и хорошими характеристиками работы, инвариантыми к масшабу и повороту: Алгоритм SIFT (Scale Invariant Feature Transform) ^[10]. Один из наиболее часто используемых алгоритмов описания особых точек. Точки, полученные с помощью алгоритма, устойчивы к изменениям освещения, шумам и изменениям позиции наблюдателя. Характеризуется приемлемой вычислительной эффективностью. Алгоритм SURF (Speeded Up Robust Features) ^[11]. Методика основана на поиске особых точек, при этом для каждой точки считается градиент максимального изменения яркости и коэффициент масштабирования по матрице Гессе. Метод RIFF (Rotation Invariant Fast Features) ^[12]. В основу метода положено радиальное и тангенциальное разложение гистограмм градиента и последующая обработка по кольцам. Дескриптор также инвариантен к изменению освещенности.

В настоящей работе исследуются алгоритмы распознавания изображений изменчивых по структуре сгущений малоразмерных объектов в двумерном или трехмерном пространстве, когда априори не известно какие отметки в наблюдаемой сцене из смеси с шумом, составляют распознаваемые группы, сколько их и каких классов, неизвестна их ориентация, а иногда и масштаб изображения.

Рагистрация и синтез изображений полученых по средствам разных регистрируемых технологий не всегда способны передать форму и детально описать исследумые объектов в наобходимом качестве. Это может происходить, например, от недостатка разрешающей способности аппаратуры, шумов и других условий. Поэтому часто объекты интереса могут быть преставлены точечными объектати (ТО) или групповыми точечными объектами (ГТО). Предполагается, что задачи обнаружения отдельных ТО и пространственной локализации ГТО решены, например, одним из рассмотренных подходов выше.

В задачах распознавания образов групповые точечные объекты (ГТО) представляют собой множества изолированных точек в непрерывном или дискретном пространстве заданной размерности. Для их моделирования предполагается использовать пространственные элипсоиды (1), которые определяются заданной плотностью ТО.

`x^2/a^2 + y^2/b^2 + z^2/c^2 = 1,` (1)

где полуоси элипсоида.

На рис.1, а предсталена моделируемая сцена, которая состоит из смеси ТО и ГТО.

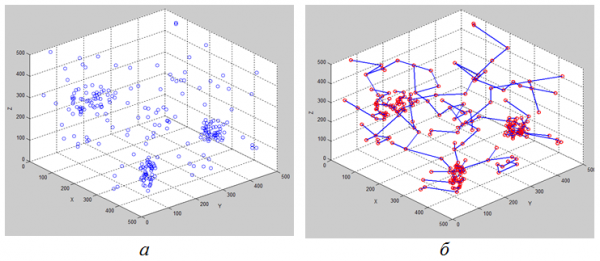
Рис. 1. Моделирование ГТО и ТО

Важнейшим информативным признаком, отличающим область расположения ГТО от фона из ложных отметок, служит более высокая плотность точечных объектов. Для представления и дальнейшей обработки предполагается решить задачу построения минимального остова ^[13,14] на множестве точек (рис.1, а).

Пусть в трехмерном пространстве задана функция расстояния между ТО этого пространства и конечное множество точек V, которые могут рассматриваться, как вершины графа. Отрезки, соединяющие точки из V могут рассматриваться, как ребра некоторого неориентированного графа, а расстояние между этими точками, весом соответствующих ребер. Тогда задача построения минимального охватывающего дерева имеет следующую формальную постановку.

Пусть имеется связный неориентированный граф G = (V, E), в котором V – множество ТО, E – множество ребер. Для каждого ребра графа (u,v) задан неотрицательный вес w(u,v), измеряемый эвлидовой метрикой. Задача состоит в нахождении подмножества T Ì E, связывающего все вершины, для которого суммарный вес (2)

`omega(T) = sum_( (u,v)in T) omega(u,v)` (2)

минимален. Такое подмножество T можно считать деревом. Минимальным покрывающим деревом называют покрывающее дерево, имеющее минимально возможный вес ^[15].

Наиболее известными алгоритмами построения минимального остовного дерева являются алгоритмы Крускала, Прима и Борувки ^[16]. Лучшее время работы алгоритма Крускала составляет O(E * logE), а лучшее время работы алгоритма Прима O(E * V * logV) и для алгоритма Борувки O(E * logV), где |V| - количество вершин графа G , |E| - количество ребер графа G.

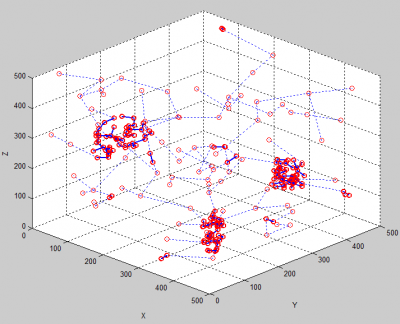
Рис. 2. ГТО после удаления длиных ребер пороговым значением.

Для реализации и построения минимального оставного дерева был взят алгоритм Крускала. На рис. 2 предавлена сцена из ГТО после пороговой обработки минимального оставного дерева, где хорошо видно, как пространственные ГТО выделяются в изолированные оставы.

В модель наблюдаемого изображения – результат обнаружения точечных объектов, введем дополнительный математический объект – ассоциированный сплошной образ (АСО). АСО представляет собой новый объект, полученный посредствам увеличения радиуса ТО до некоторого значения, при котором ГТО начинает рассматирваться, как единый объект. На рис. 3 представлен процесс моделирования АСО из ТО с ростом внутреннего радиуса ТО.

Для построения объекта АСО используется алгорим заполнения области с затравкой ^[17]. Сложность такого алгоритма сотавляет O(N), где N – размерность области заливки.

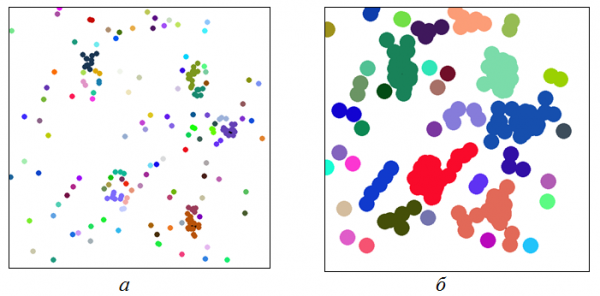
Рис. 3. АСО с разным внутренни радиусом для ТО.

Исследования показывают, что внутренний радиус ТО при некотом значении, объединяет ГТО в единый объект (АСО) при этом такие объеты имеют большую площать, по сравнению с шумовыми ТО. Результат такой обработки можно пронаблюдать на рис.4. Для статистически однородных по плотности ГТО и соответствующих им однородных по яркости АСО вся яркостная информация об объекте сосредоточена равномерно.

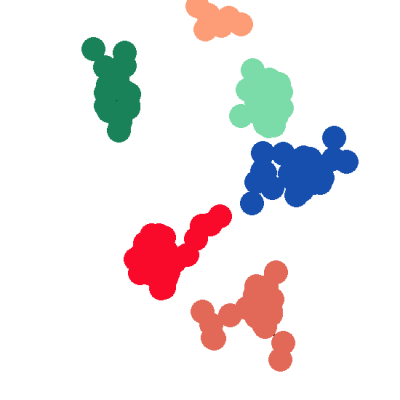
Рис. 4. Объекты АСО после пороговой обработки.

Для исследования зависимости количества объекто АСО от внутренненго радиуса ТО построим график (рис.5). Анализ графика показывает, что число объектов будет уменьшаться по обрано пропорциональной завизависимости. Дальнейшее распознавание АСО можно реализовать по информативным признакам контуров, площади и другим характеристикам.

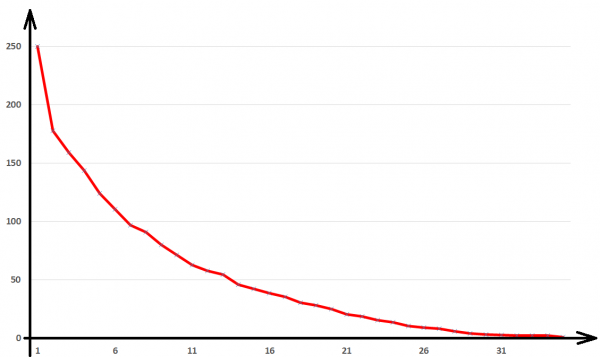
Рис. 5. Зависомость числа объектов АСО от радиуса ТО.

Таким образом, в работе выли исседованы алгоритмы обнаружения ГТО на основе минимального оставного дерева (MST) и с использованием модели ассоциированного сплошного образа (ACI).

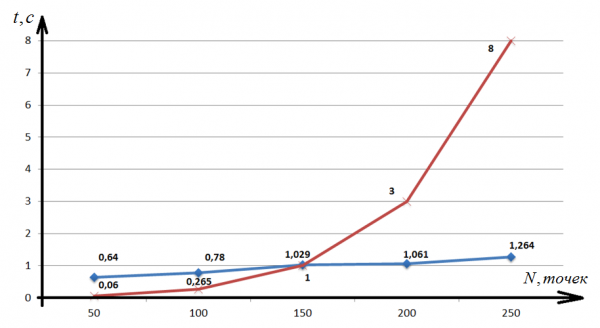
Рис. 6. Временные характеристики для алгоритмов MST и ACI.

Из графика рис.6 видно, что алгоритм ACI имеет линейную сложность, а алгоритм MST экспоненциальную. При этом до некоторой размерности скорость работы алгоритмов будут примерно сопоставимы. Созданные алгоритмы подверждаются теоретическими и практическими рассчетами ^[18-20].